Примеры

1. Функция задается в виде зависимости между двумя индексными переменными (массивами) по значению индексной переменной, определяющей позиции соответствующих элементов, принятых в качестве функции и аргумента (см. рис.3.2).

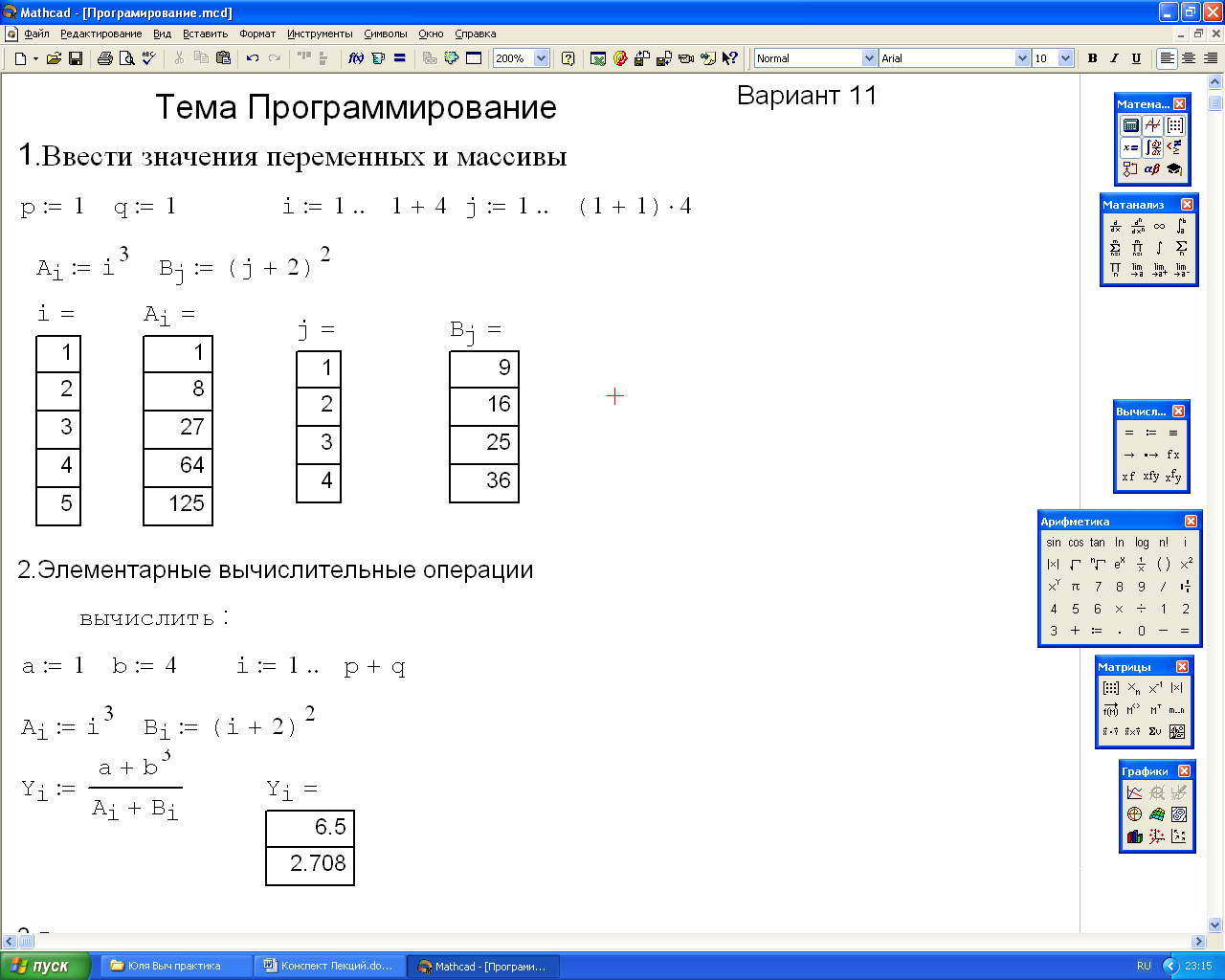
Рис. 1. Табличная форма задания функций.

2. Операторы цикла

Вложенные циклы программируются с помощью операторных скобок

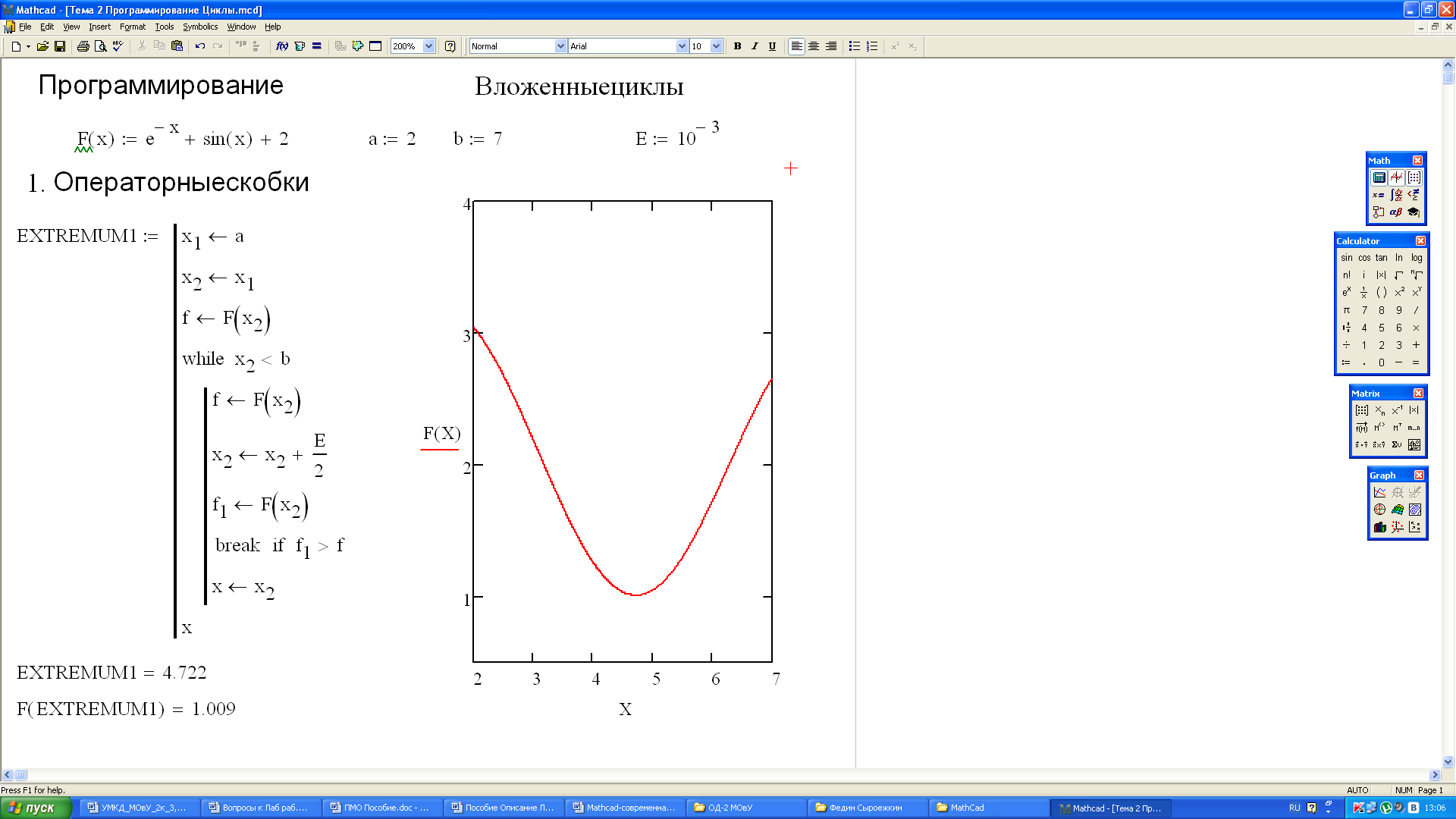
Рис. 2. Вложенные циклы..

2. Визуализация функций Аналитическая форма скалярной функции векторного аргумента также представлена на рис 3.3.

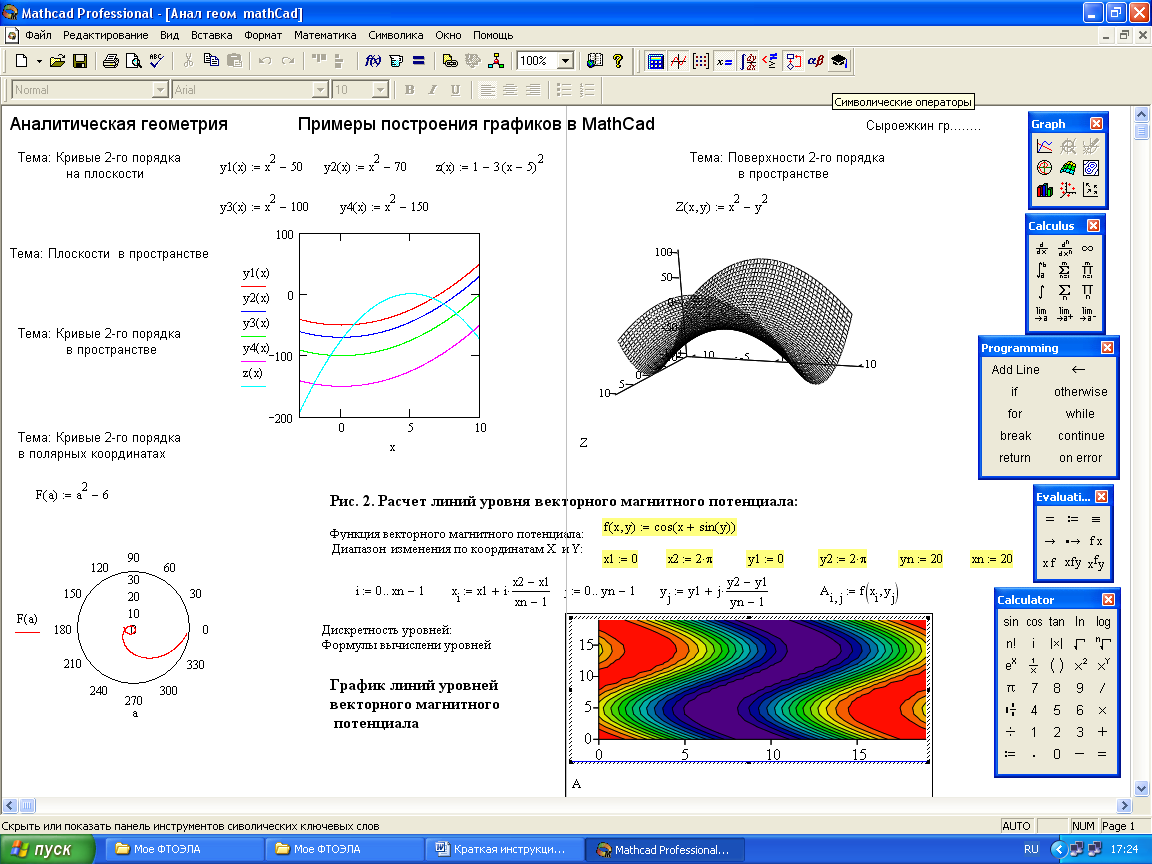
Рис. 3. Аналитическая форма задания векторной функций скалярного аргумента и скалярной функции векторного аргумента.

3. Вычисление частных производных и градиента в MathCad может быть реализовано также в аналитической форме с помощью символьной математики. Пример вычисления частных производных построения градиента функции в аналитической форме приведен на рис 4.2.

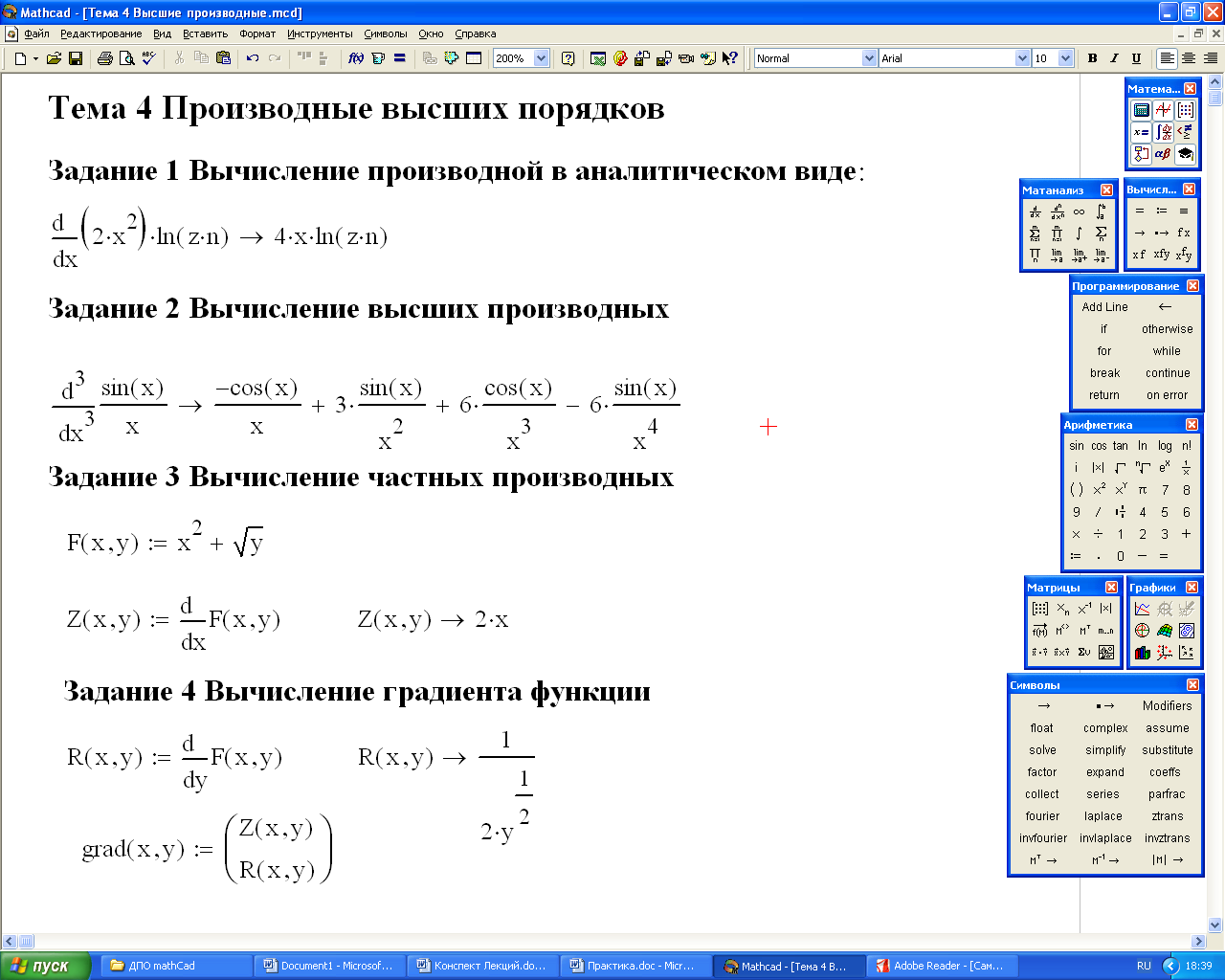
Рис.4. Аналитическая форма задания скалярной функции векторного аргумента и векторной функции векторного аргумента (градиента).

4. Матричный аппарат MathCad Понятие матрицы. Размер матрицы. Квадратная, симметричная, диагональная, единичная матрицы. Подменю матричной алгебры в MathCad.

Рис.5. Матричный аппарат MathCad линейной алгебры.

3. Описания к лабораторным работам

Работа №1. Метод равномерного поиска

Задание

1. Ознакомиться с алгоритмом машинного метода одномерной оптимизации равномерного поиска.

2. Составить программу метода и отладить на контрольном примере.

3. Рассчитать экстремум функции, заданной по варианту, и сопоставить точку экстремума с точкой минимума на графике функции.

4. Произвести расчет экстремум функции для двух различных значений точности.

5. Модифицировать метод равномерного поиска, введя переменный шаг.

6. Сравнить скорость сходимости метода равномерного поиска с постоянным и переменным шагом.

Методические указания

1. Среди одномерных методов поиска экстремума целевой функции наиболее простыми является метод равномерного поиска. Описание метода приведено в разделе 3, тема3.

Названный метод требует задания целевой функции F(х) и начального интервала (a,b), на котором заданная функция унимодальна. Алгоритм позволяет уменьшить начальный интервал до некоторого конечного (х_1, х₂ ) < δ, где δ – заданная точность.

Блок-схема машинного алгоритма метода равномерного поиска приведена на рис. 22. В качестве машинных переменных, соответствующих текущему значению параметра оптимизации на i-ом и (i+1)-ом шаге использованы идентификаторы х и х₁, а для значений целевой функции F, F₁ соответственно. Оптимальное значение параметра по завершении расчета содержится в х, целевой функции в F.

Ввести F(х), a, b, e

Присвоить х₁= х = a

Вычислить F = F(х)

Присвоить х = х + δ /2 ; F₁ = F(х)

Вычислить F = F(х)

Если F₁ > F, то идти к 9

Н ет

Да

Присвоить х₁ = х, F = F₁

Н

Если х <,b, то идти к 3

ет

Д а

Печать х, F(х)

Конец

Рис. 23. Блок-схема алгоритма метода равномерного поиска.

2. На основании блок-схемы алгоритма составляется программа в Mathcad. Текст программы и отладочный пример приведены на рис. 24 (скриншот).

Входными данными программы являются целевая функция F(х), начальный интервал (a,b) и δ – точность по параметру оптимизации.

Программа вводится согласно правилам, приведенным в разделе 4. Далее производится отладка программы на примере целевой функции и параметров, приведенных на рис. 23. Там же построен график целевой функции F(х) для отладочного примера, который демонстрирует, что данная функция унимодальна на заданном интервале (а, в).

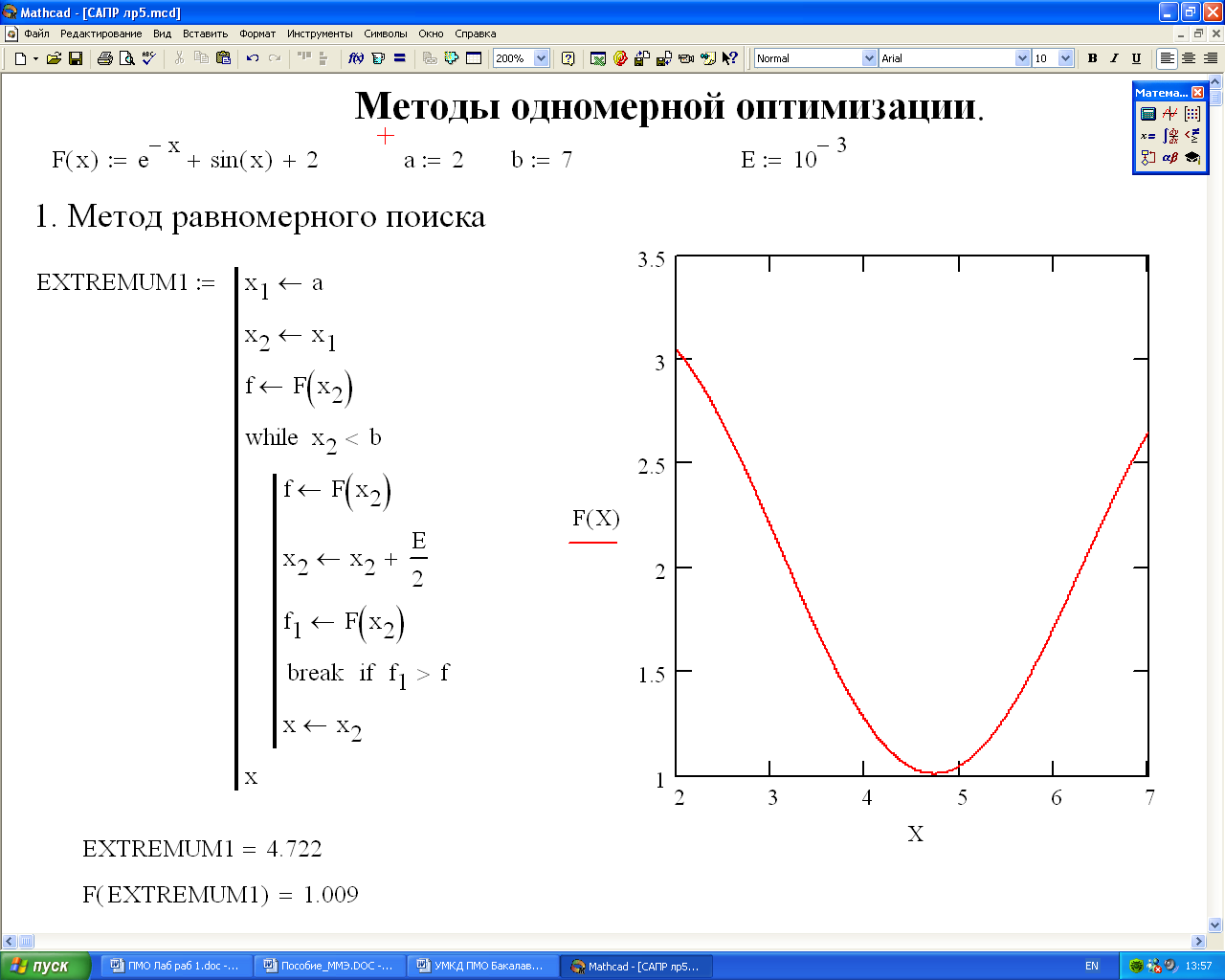
Рис. 24. Программная реализация метода равномерного поиска в Mathcad.

3. Для выполнения задания нужно ввести в программу функцию, соответствующую варианту задания и заданному интервалу, и произвести расчет точки экстремума с заданной точностью. Варианты целевых функций, а также значения параметров для расчетов согласно вариантам заданий приведены в таблице 3.

Таблица 3. Варианты заданий

Номер варианта	Целевая функция F(x)	Интервал (а,b)	Точность e
1	4 – 0,1х + cos(x)	0 – 5,0	0,01
2	х² + 1/х	0,1 – 2,0	0,001
3	tg(x) + 1/х	0,1 – 1,5	0,0001
4	exp(x) + 1/х	0,1 – 1,0	0,001
5	tg(x) – ln(x)	0,1 – 1,0	0,0001
6	3۰exp(–x) + sin(x)	0 – 8,0	0,01

Рассчитанное значение экстремума функции (точку экстремума) необходимо сопоставить с точкой минимума на графике функции.

4. С целью оценки влияния точности на точку минимума необходимо, уменьшив порядок точности на единицу, произвести расчет экстремума функции и сопоставить значение точки экстремума для двух различных значений точности.

5. Чтобы модифицировать метод равномерного поиска, введя переменный шаг, необходимо ввести в программу формулу расчета шага: h := 0,1۰k۰h , где (для k принять значение номера варианта) и логическую переменную R, значение которой присвоить равным 2, пока выполняется условие F₁ > F, и значение 0,5 – в противном случае.

6. Для того, чтобы сравнить скорость сходимости метода равномерного поиска с постоянным и переменным шагом, нужно вставить в цикл программы счетчик и оценить скорость сходимости по числу циклов.