
- •Типовой расчет “функции нескольких переменных” Основные понятия
- •Дифференцирование функций нескольких переменных Частные производные функции
- •Экстремумы функции
- •Контрольные варианты к задаче 2.
- •Наибольшее и наименьшее значения функции в замкнутой области d
- •Контрольные варианты к задаче 3.
- •Элементы скалярного поля
- •Контрольные варианты к задаче 4.
Типовой расчет “функции нескольких переменных” Основные понятия
Определение функции двух переменных
 ,
или
,
или
 .
.Способы ее задания: аналитический, табличный, явный, неявный.
Область определения и область изменения функции
 .
Классификация областей определения:
открытая и замкнутая, ограниченная и
неограниченная.
.
Классификация областей определения:
открытая и замкнутая, ограниченная и
неограниченная.Геометрический смысл функции , или
 .
.
Пример
1. Найти
область определения функции
![]() .
.
Решение. Функция
z представляет собой сумму двух
слагаемых функций:
![]() и
и
![]() .
Найдем области их определения:
.
Найдем области их определения:
|
|
|
|
Очевидно,
область определения функции z
есть
пересечение
областей определения
![]() ,
т. е.
,
т. е.
![]() (рис. 1).
(рис. 1).
-2 0 2 x
Рис. 1 |
Ответ: D – область, отмеченная двойной штриховкой, замкнутая и неограниченная. |
Пример
2. Найти
область определения функции
![]() .
.
Решение.
z
– логарифмическая функция, поэтому
![]()
L
D С(-1, 0) 0 x
Рис. 2
|
Парабола разбивает всю плоскость на две части: внутреннюю и внешнюю по отношению к параболе. Возьмем для контроля любую точку плоскости, например, О(0, 0), подставим |
ее
координаты в первое неравенство:
![]()
![]() ;
где D
– область определения функции, открытая,
неограниченная (рис.2).
;
где D
– область определения функции, открытая,
неограниченная (рис.2).
Дифференцирование функций нескольких переменных Частные производные функции
а)
первого порядка:
![]() ,
,
где
![]() - частное приращение
z
по х.
- частное приращение
z
по х.
![]() ,
,
где
![]() - частное приращение
z
по y.
- частное приращение
z
по y.
б)
второго порядка:
![]() - вторая производная функции z
по переменной x,
т. е. частная производная по переменной
х,
взятая от частной производной первого
порядка по переменной х.
- вторая производная функции z
по переменной x,
т. е. частная производная по переменной
х,
взятая от частной производной первого
порядка по переменной х.
![]() -
смешанная производная z
по х
и по у;
-
смешанная производная z
по х
и по у;
![]() -
смешанная производная z
по у
и по х.
-
смешанная производная z
по у
и по х.
Можно
показать, что порядок дифференцирования
безразличен, т. е.
![]() ;
;
![]() -
вторая производная функции z
по переменной
y.
-
вторая производная функции z
по переменной
y.
Правило. Отыскивая частные производные функции нескольких переменных по одной из переменных, пользуемся правилами и формулами дифференцирования, считая в этот момент все остальные переменные постоянными.
Задача 1. Найти частные производные первого порядка следующих функций:
а)
![]() .
.
![]()
 ,
,
отыскивая
![]() ,
переменную у
считаем постоянной.
,
переменную у
считаем постоянной.
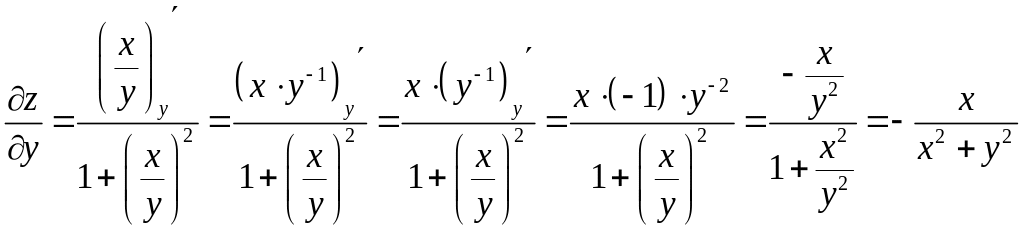 ,
,
отыскивая
![]() ,
переменную х
считаем постоянной.
,
переменную х
считаем постоянной.
б)
![]() .
.
![]()
отыскивая , переменную у считаем постоянной.

отыскивая , переменную х считаем постоянной.
Пример 1. Доказать следующие тождества:
а)
![]() ,
если
,
если
![]() .
.
Решение.
Найдем
![]() данной функции и подставим их в равенство,
которое надо доказать:
данной функции и подставим их в равенство,
которое надо доказать:

отыскивая , переменную у считаем постоянной..
 ,
,
отыскивая , переменную х считаем постоянной.
Следовательно

что и требовалось доказать.
Пример
2. Найти
![]() и
и
![]()
![]() функции
функции
![]() .
.
Решение
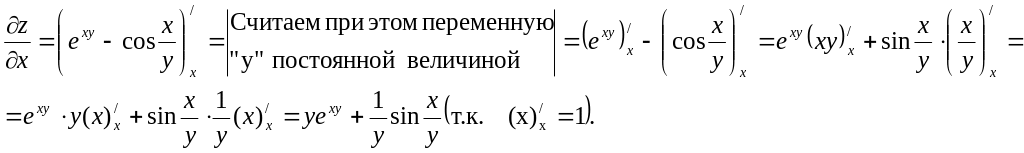
 Ответ:
Ответ:
![]()
Пример
3. Найти
частные производные второго порядка
функции
![]() .
.
Решение.


Таким
образом:![]() ,
,
![]() ,
,



Таким
образом:![]()
![]()
Заметим,
что
![]()
Контрольные задания к задаче 1
ЗАДАНИЕ
1а.
Найти
![]() и
и
![]() функции:
функции:
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
11.
|
12.
|
13.
|
14.
|
15.
|
16.
|
17. |
18. |
19. |
20. |
21. |
22. |
23. |
24. |
25. |
26. |
27. |
28. |
29. |
30. |
ЗАДАНИЕ № 1 б. Найти и функции:
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
11.
|
12.
|
13.
|
14.
|
15.
|
16.
|
17. |
18. |
19. |
20. |
21. |
22. |
23. |
24. |
25. |
26. |
27. |
28. |
29. |
30. |
Пример
4. Показать,
что
![]() при
при
![]() .
.
Решение. Сначала найдем первые частные производные




Теперь находим смешанные вторые частные производные и сравниваем их.

![]() Видим,
что смешанные производные равны, что и
требовалось показать.
Видим,
что смешанные производные равны, что и
требовалось показать.

 y
y y
y











