Глава 7 пограничный слой. Аэродинамический нагрев
Сопротивление удобообтекаемых тел при их движении в жидкостях или газах является в значительной степени сопротивлением от трения среды о поверхность тела. Поэтому весьма важно знать законы трения в жидкостях и газах и уметь рассчитывать сопротивление трения. Установлено, что силы трения жидкости проявляются не во всей среде, а лишь в слое, прилегающем к поверхности движущегося тела, где скорость течения резко изменяется по нормали к поверхности.
В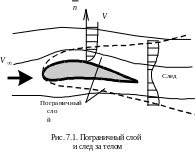
отличие от идеальной жидкости, которая
при своем движении скользит по обтекаемой
поверхности, реальная вязкая жидкость
полностью затормаживается на ней.
Частицы, прилегающие к поверхности
обтекаемого тела, сцепляясь с ней,
тормозят вышележащие слои жидкости.
Вследствие этого вблизи поверхности
скорость жидкости изменяется от
на стенке до скорости набегающего потока
или скорости потенциального течения
на некотором расстоянии от нее. Даже
при движении жидкостей, вязкость которых
незначительна (вода, воздух), подобное
нарастание скорости совершается
достаточно быстро. В результате, у
поверхности тела, обтекаемого маловязкой
жидкостью, есть очень тонкий слой,
называемый пограничным
слоем.
Пограничный слой (рис. 7.1) представляет
собой область больших значений градиентов
скорости по нормали к поверхности.
Внутри пограничного слоя сила вязкостного
трения имеет такой же порядок, как и все
остальные силы, учитываемые в уравнениях
движения.
Уравнения Навье–Стокса
Запишем уравнение движения (3.8) с учетом внутреннего трения в следующем виде:
.
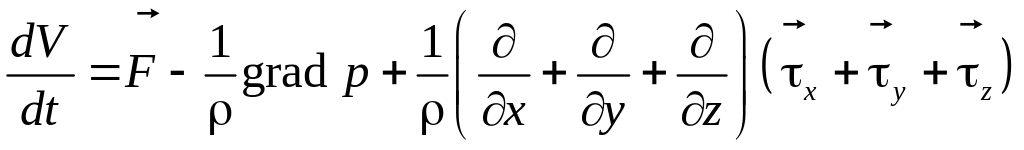(7.1)
Напомним,
что
представляют собой касательные напряжения
от силы трения, действующие на площадки,
перпендикулярные соответствующим осям
координат. Каждая из этих составляющих,
в свою очередь, может быть представлена
в виде суммы трех проекций на оси
координат. Таким образом, мы имеем тензор
напряжений (3.10), симметричный относительно
главной диагонали, т. е.
,
,
.
Составляющие тензора напряжений можно выразить с помощью обобщенного закона Ньютона (3.12):
,
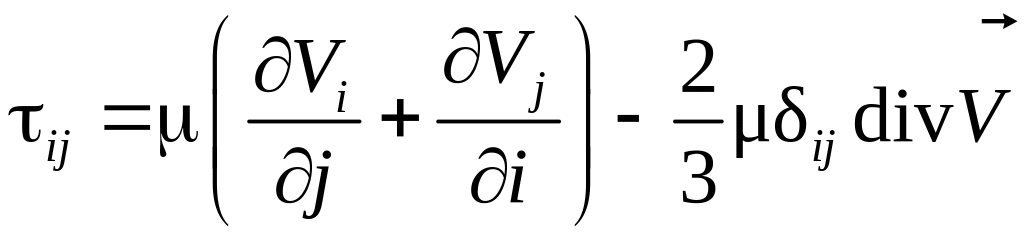где
имеет вид телеграфного сигнала (или
единичной матрицы), принимая значения
при
или
при
;
и
– координатные направления.
Тогда, например:
,
.
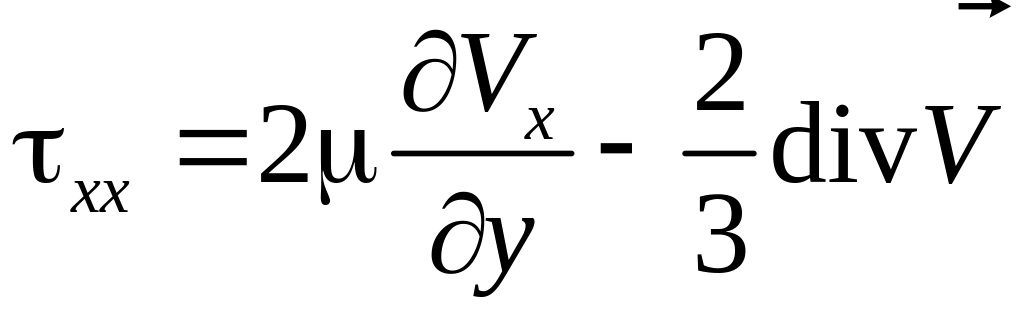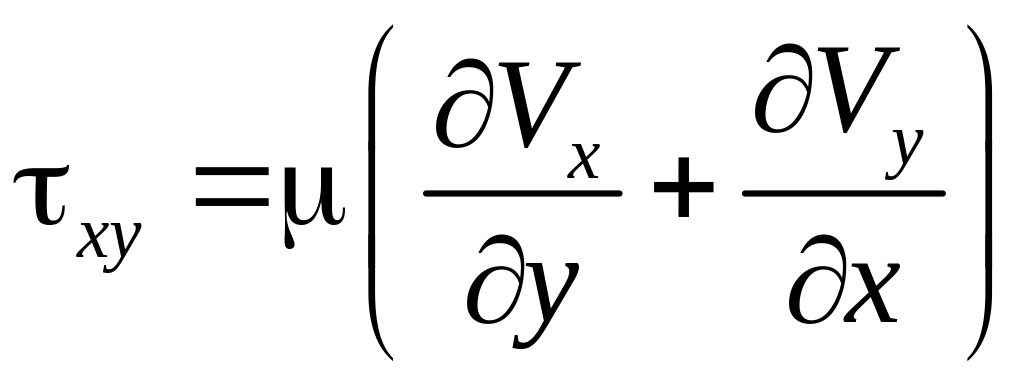С
учетом выражений (3.10) для
,…,
расписав каждую из составляющих
тензора напряжений, запишем уравнение
движения (7.1) в проекциях на оси координат:
(7.2)
Уравнения (7.2) и
есть уравнения Навье–Стокса. В общем
случае коэффициент вязкости
зависит от температуры. Если считать
,
то уравнения Навье–Стокса будут иметь
вид
,
,
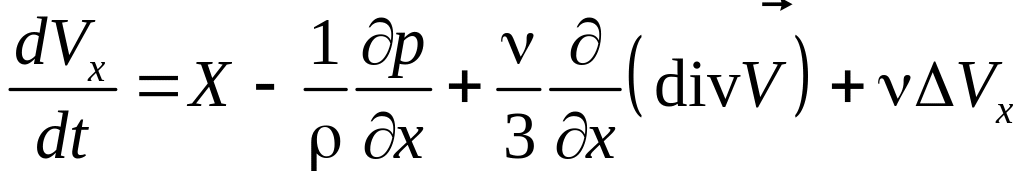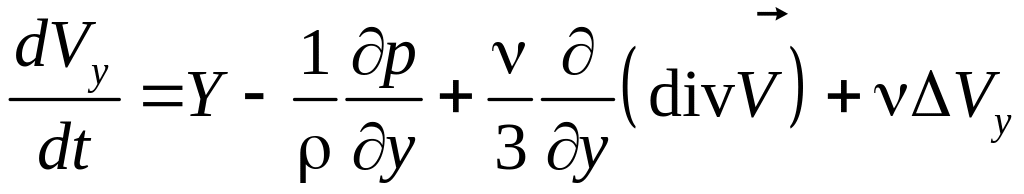(7.3)
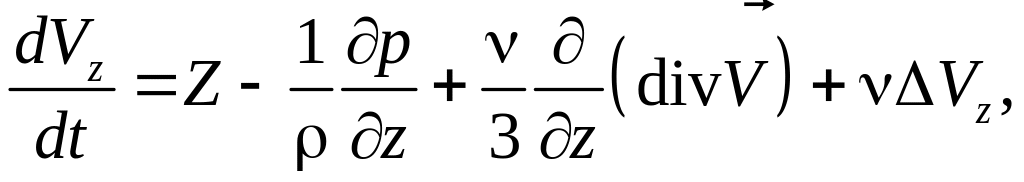
где
– оператор Лапласа.
Точное решение задачи обтекания какого-либо тела, сводящееся к интегрированию сложных дифференциальных уравнений при заданных граничных условиях, представляет огромные трудности. Для получения каких-либо частных решений прибегают к упрощению дифференциальных уравнений.
Так Д. Стокс, решая
задачу об обтекании шара потоком вязкой
жидкости и сделав допущение о малости
инерционных членов, отбросил их полностью.
Однако такое упрощение справедливо
только при очень малых числах Рейнольдса,
незначительно отличающихся от единицы.
О. Рейнольдс принял модель несжимаемой
жидкости, отбросив полностью инерционные
члены, а из вязких членов оставил
главнейшие. Этот метод применяется при
решении гидродинамических задач теории
смазки (при малых числах
).
Другие авторы вместе с вязкими членами
оставили в уравнении только важнейшие
из инерционных членов, которые к тому
же линеаризируются путем замены
неизвестной скорости перед производной
ее характерным значением. Однако и этот
метод применим при небольших числах
и к тому же достаточно сложен.
При изучении обтекания тел при больших числах Рейнольдса, характерных для авиационной и ракетной техники, применяют метод упрощения уравнений Навье–Стокса, основанный на понятии пограничного слоя.