Глава 3 уравнения движения газа как сплошной среды
Уравнения движения выводятся исходя из закона сохранения массы, закона изменения количества движения, закона сохранения энергии, уравнения термодинамического состояния и уравнения напряженного состояния.
Применим эти законы к массе жидкости m, находящейся в момент времени t в некотором произвольно выделенном объеме V. Будем считать, что внутри объема нет ни источников, ни стоков.
Уравнение неразрывности
Согласно
закону сохранения массы для изолированной
системы, масса жидкости m,
которая находилась в момент времени t
в рассматриваемом объеме, будет оставаться
неизменной при ее движении. То есть
и
.
И
зменение
массы при движении может происходить
как за счет изменения плотности
с течением времени, так и за счет изменения
объема V,
который может занимать рассматриваемая
масса жидкости в следующий момент
времени. Изменение массы за счет изменения
плотности запишется как
.
Найдем
изменение массы за счет изменения
объема. Элемент поверхности dS
рассматриваемого объема переместится
за время
на расстояние
(рис. 3.1); за счет перемещения элемента
поверхности объем изменится в единицу
времени на
.
Тогда изменение массы равно
.
Поскольку суммарное изменение массы
равно нулю, то получаем
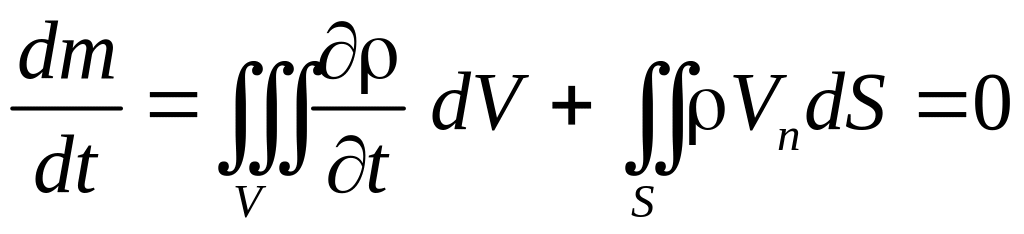– закон сохранения массы в интегральной
форме.
Преобразуем интеграл по площади в интеграл по объему с помощью формулы Остроградского–Гаусса:
.
Объединяя
интегралы, получим
.
В силу произвольности элементарного
объема
это равенство возможно, если подынтегральное
выражение равно нулю, т. е. если
. (3.1)
Выражение (3.1) представляет собой закон сохранения массы в дифференциальной форме, или иначе – уравнение неразрывности для неустановившегося движения сжимаемой жидкости. Для установившегося движения сжимаемой жидкости уравнение неразрывности имеет вид
. (3.1а)
Приведем уравнение (3.1) к другой форме, произведя следующие преобразования:
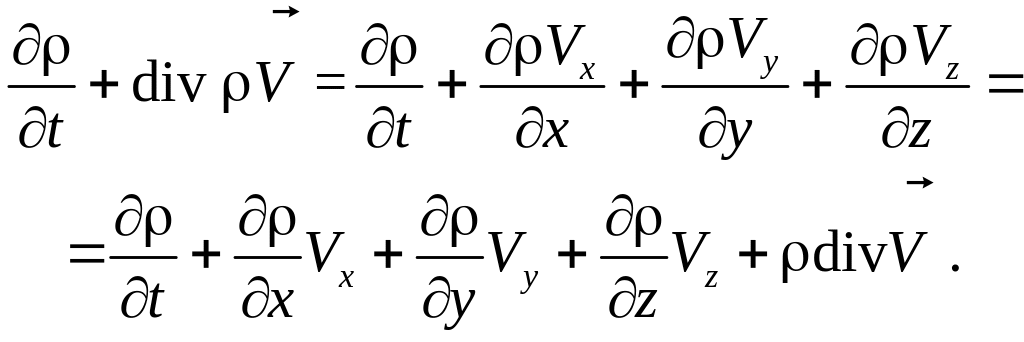
Так
как
,
то уравнение неразрывности примет вид
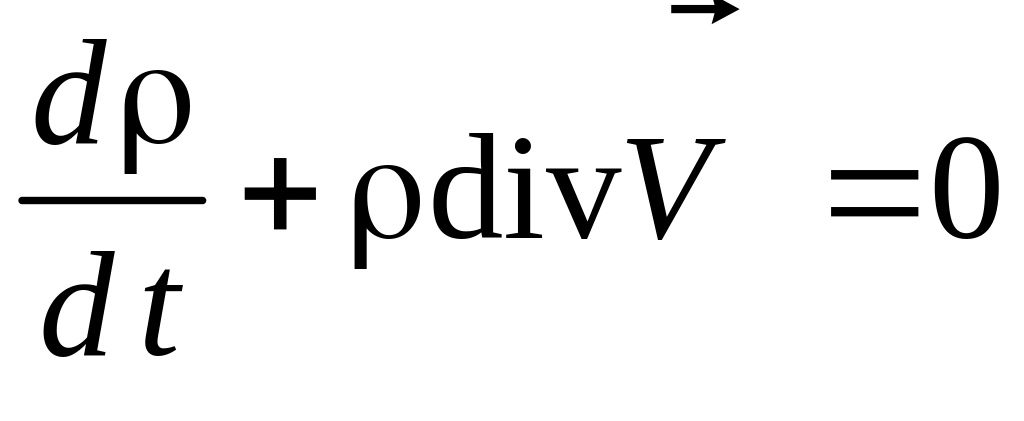. (3.1б)
В
случае движения несжимаемой жидкости
(
)
запись уравнения неразрывности еще
более упростится:
. (3.1в)
Если
движение несжимаемой жидкости
потенциальное, то проекции вектора
скорости на координатные направления
можно записать через потенциал вектора
скорости
как
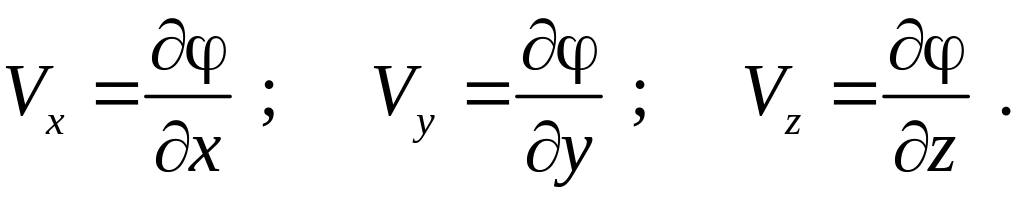
Тогда
.
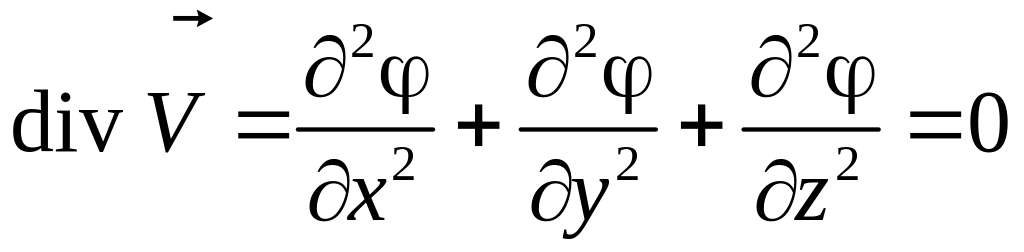Так как
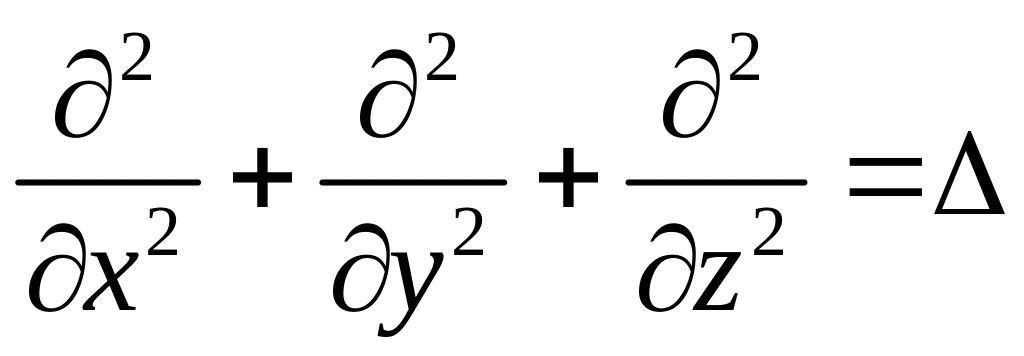– это оператор Лапласа, то уравнение
неразрывности для случая потенциального
движения несжимаемой жидкости
преобразуется в уравнение Лапласа:
. (3.1г)
В случае установившегося движения газа при решении практических задач часто используется уравнение неразрывности в форме уравнения массового расхода:
, (3.2)
где F – площадь поперечного сечения трубки тока, или (при движении несжимаемой среды) в форме объемного расхода:
. (3.2а)
Формулы (3.2) и (3.2а) получаются элементарным образом при рассмотрении расхода сжимаемой и несжимаемой жидкости через поперечные сечения трубки тока.
Уравнение, выражающее закон изменения количества движения
Согласно
закону изменения количества движения
изменение вектора количества движения
постоянной
массы m
(находящейся
в объеме V
в момент времени t)
равно сумме внешних сил, действующих
на рассматриваемую массу:
.
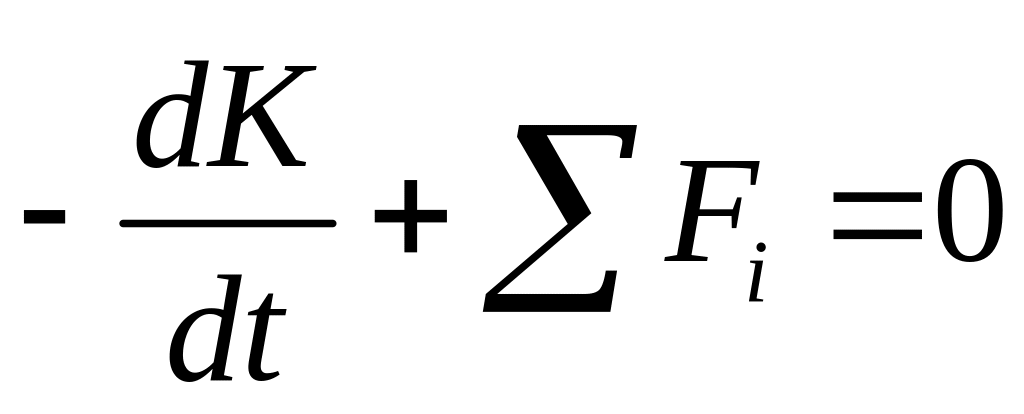(3.3)
Внешние силы, способные изменить количество движения данной массы жидкости, разделяют на объемные и поверхностные силы.
Объемные
силы – силы,
величина которых пропорциональна массе
жидкости в выделенном объеме. В данном
случае имеет место сила тяжести, равная
,
где
– главный вектор массовых сил, отнесенных
к единице массы, т. е. ускорение от
массовых сил (наиболее простое
представление – ускорение силы тяжести).
Поверхностные
силы – силы,
величина которых пропорциональна
площади поверхности, охватывающей
выделенный объем. К ним относятся силы
от нормальных и касательных напряжений,
действующих на поверхность частицы.
Считая жидкость идеальной, ограничимся
рассмотрением только силы от
аэродинамического давления, которая
направлена по внутренней нормали. Тогда
для внешней нормали
коэффициент давления
,
и сила, действующая на всю поверхность,
равна
.
Если
есть ускорение элемента dV,
то сила инерции (вектор изменения
количества движения) равна
.
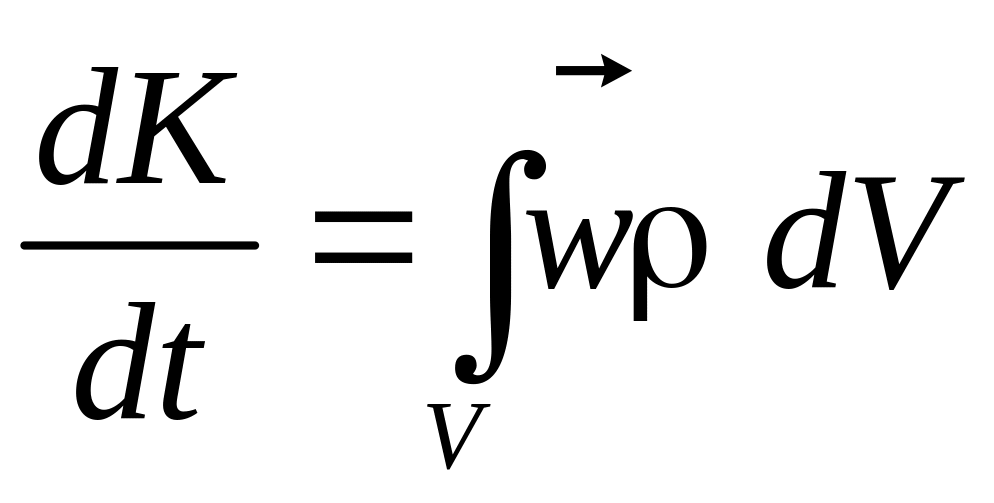Подставляя все в уравнение (3.3), получаем уравнение движения идеальной жидкости в интегральной форме:
.
Применив
формулу Остроградского–Гаусса
,
можем объединить все три интеграла:
. (3.4)
В силу произвольности выделенного объема получаем, что подынтегральное выражение равно нулю в каждой точке газового потока в любой момент времени. Таким образом, можно прийти к уравнению движения идеального газа в векторной форме – уравнению движения Эйлера:
.
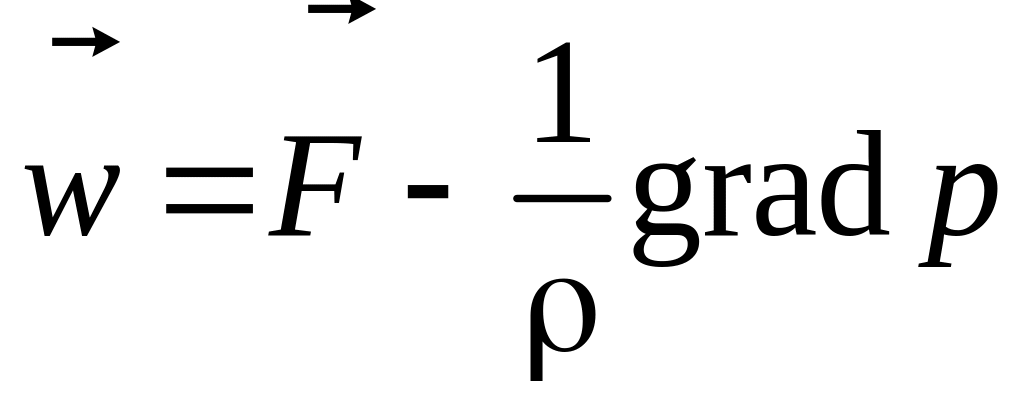(3.5)
Запишем
уравнение (3.5) в проекциях на оси декартовой
системы координат. Так как
,
,
,
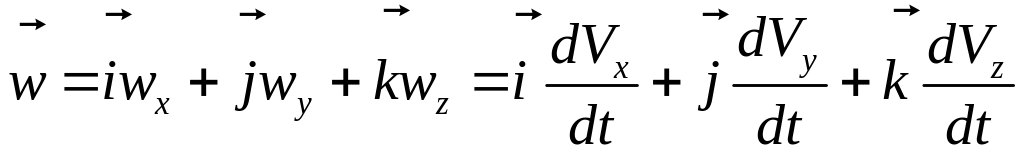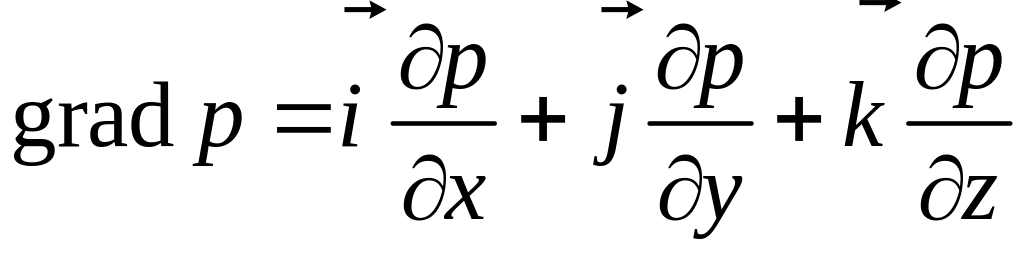то в проекциях на оси координат уравнения
Эйлера запишутся в виде
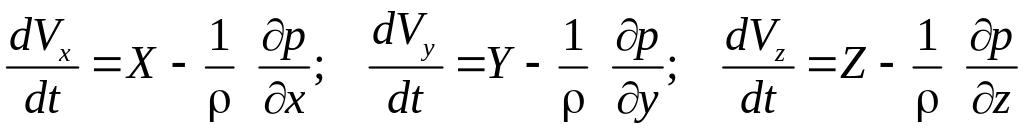. (3.6)
Уравнения (3.6) применимы для исследования движения сжимаемой и несжимаемой жидкости. Каждый член этой системы уравнений представляет собой ускорение. Можно сказать, что при движении идеальной жидкости суммарное ускорение складывается из ускорения от массовых сил и ускорения от сил давления.
Преобразуем левые части уравнений (3.6) с учетом формулы (2.3). При этом вспомним, что для проекции ускорения на ось ОХ
.
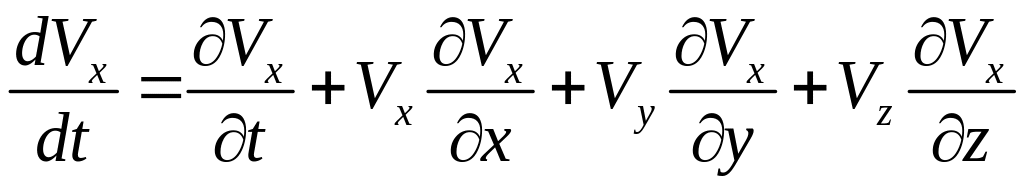Применив аналогичную запись для других проекций, получим дифференциальные уравнения Эйлера в развернутом виде:
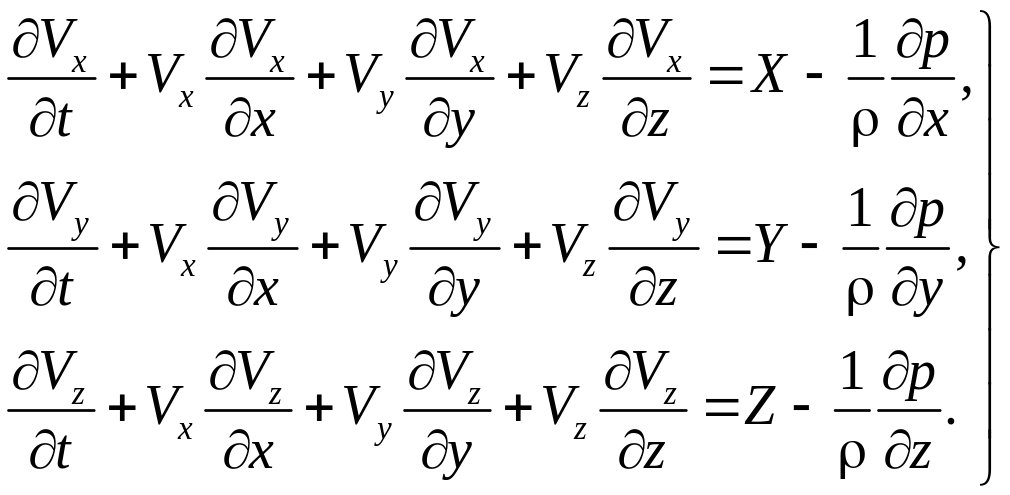(3.7)
При интегрировании дифференциальных уравнений движения газа получим решения, содержащие произвольные функции и произвольные постоянные. Для их определения необходимы дополнительные условия: начальные и граничные.
При начальных условиях задается поле скоростей в начальный для данной задачи момент времени, т. е. при t = 0:
Очевидно, что начальные условия необходимы при решении задач неустановившегося движения газа.
Граничные условия – это условия на некоторых границах течения, в качестве которых может выступать поверхность обтекаемого тела, невозмущенный набегающий поток, поверхности раздела потоков и др. Граничные условия подразделяют на динамические и кинематические.
Динамические условия относятся к силам. Например, на свободной поверхности имеет место равенство давления внешней среды и давления на обтекаемой поверхности.
Кинематические
условия относятся к скоростям. Например,
на поверхности обтекаемого тела должно
выполняться условие безотрывности
обтекания или условие непротекания
,
в силу которых вектор скорости направлен
по касательной к поверхности.
Если рассматривается движение вязкой жидкости, то в уравнениях движения необходимо учесть внутреннее трение в жидкости через силу трения:
где
– вектор силы трения, действующей на
единичную площадку,
положение
которой определяется в пространстве
нормалью
.
Согласно формуле Остроградского–Гаусса
.
Тогда уравнение (3.4) примет вид
.
После интегрирования и преобразований уравнение движения реальной жидкости в векторной форме запишется следующим образом:
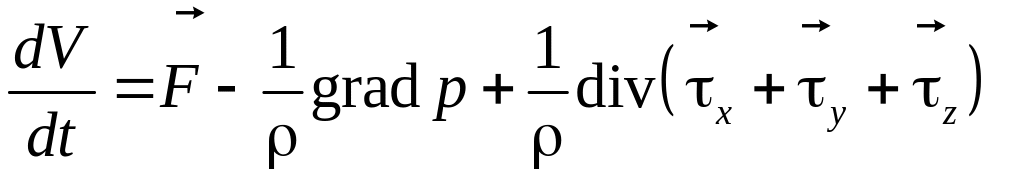. (3.8)