Интегралы дифференциальных уравнений Эйлера

В общем виде дифференциальные уравнения движения Эйлера не интегрируются. Их интегралы можно найти только для некоторых частных случаев. Рассмотрим порядок нахождения интегралов:

1) для потенциального неустановившегося движения;

2) для установившегося непотенциального движения сжимаемого газа.

Потенциальное неустановившееся движение.

Интеграл Лагранжа

Так как при потенциальном движении угловая скорость вращательного движения равна нулю, то , и из выражений (2.9) для составляющих угловой скорости имеем следующее:

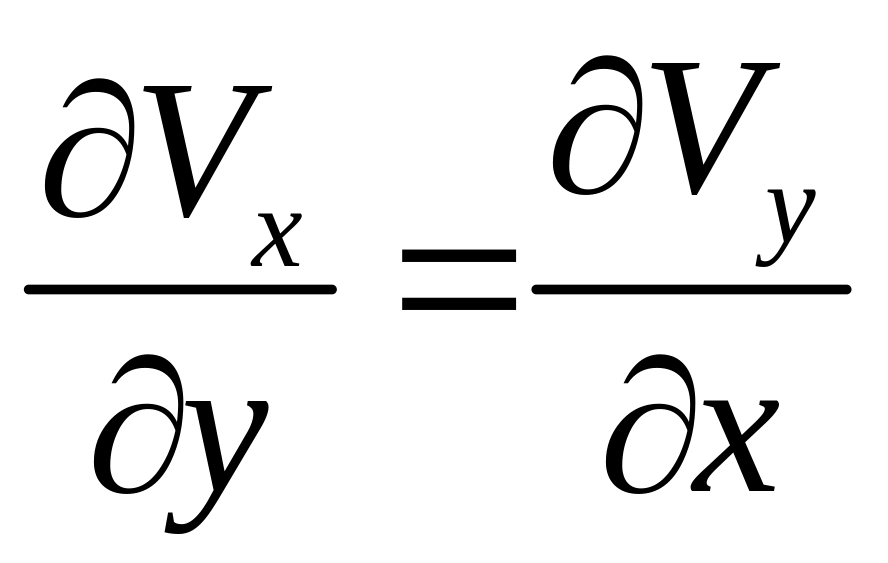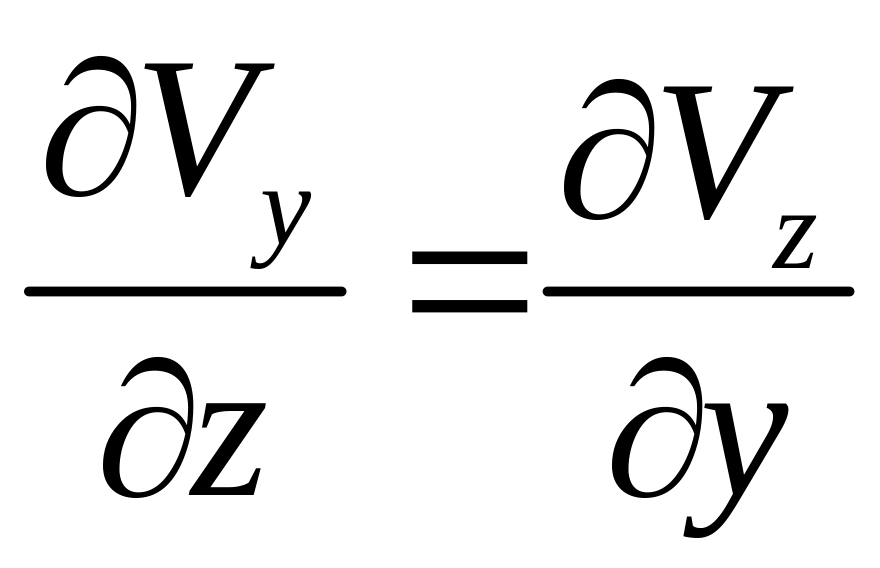, , . (3.23)

Считая жидкость идеальной, обратимся к системе уравнений Эйлера в развернутом виде (3.7). Рассмотрим уравнение в проекции на ось ОХ:

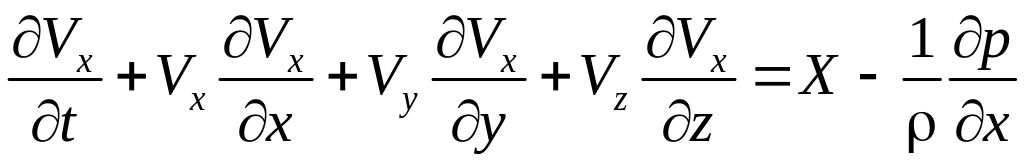. (3.24)

Принимая во внимание условия (3.23), конвективную производную в уравнении (3.24) приведем к виду

.

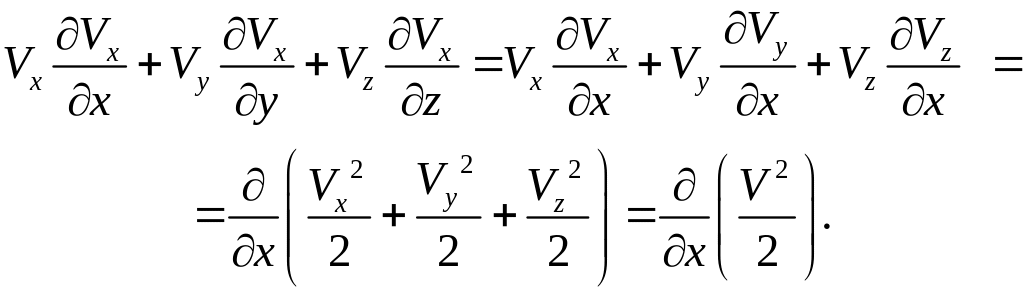Аналогичные преобразования проведем для конвективных производных уравнений в проекциях на оси ОУ и ОZ. Подставим полученные выражения в уравнения Эйлера:

, ,

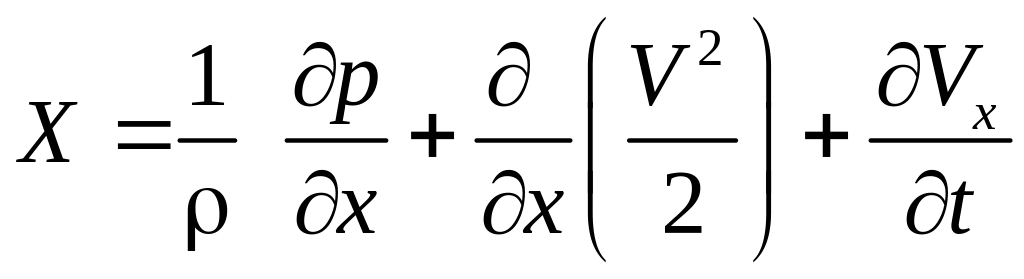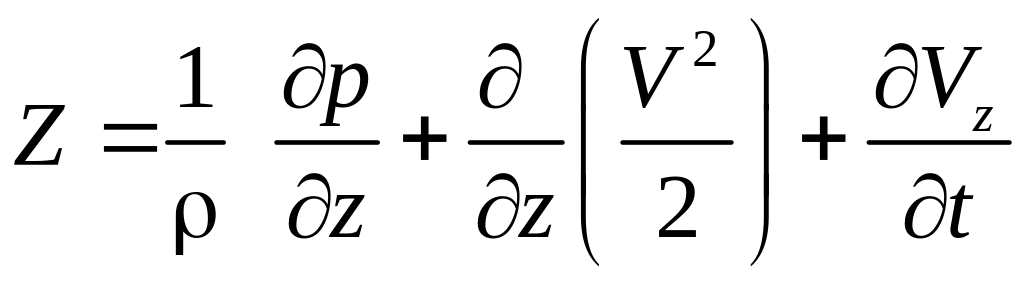. (3.25)

Преобразуем локальные производные в уравнениях (3.25), учитывая, что при потенциальном движении проекции скорости можно представить через потенциал скорости

и свойство независимости смешанной производной от порядка дифференцирования:

, ,

.

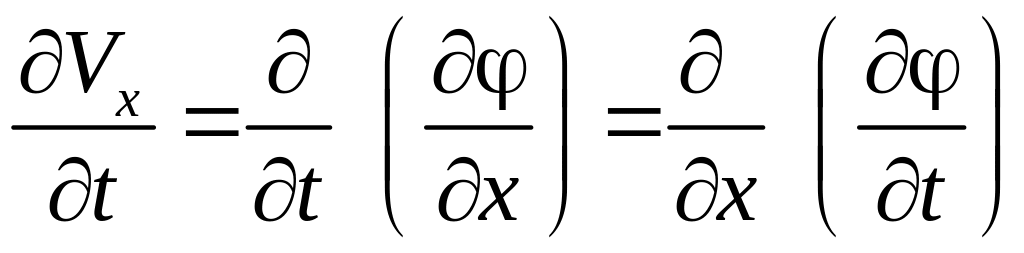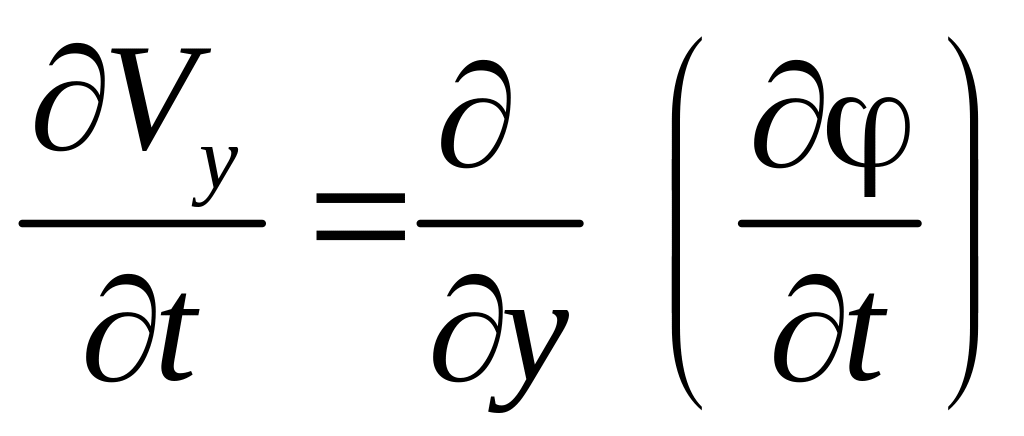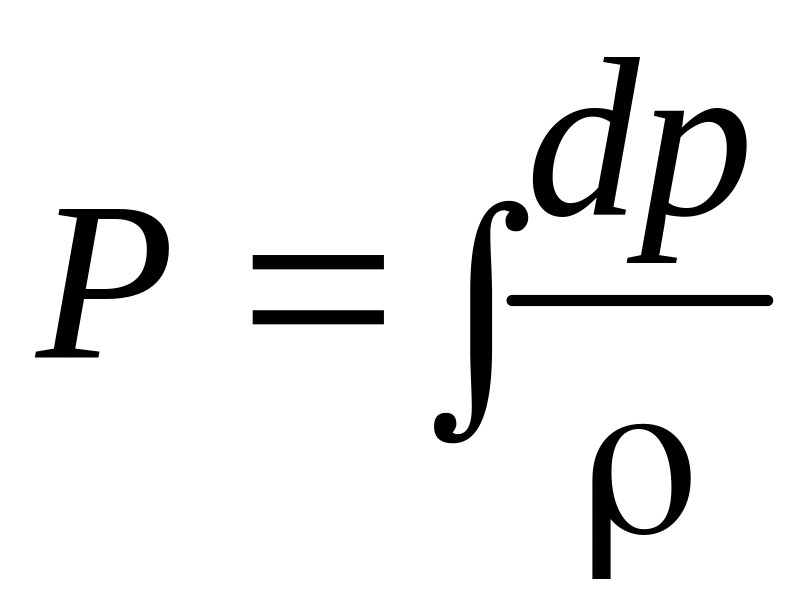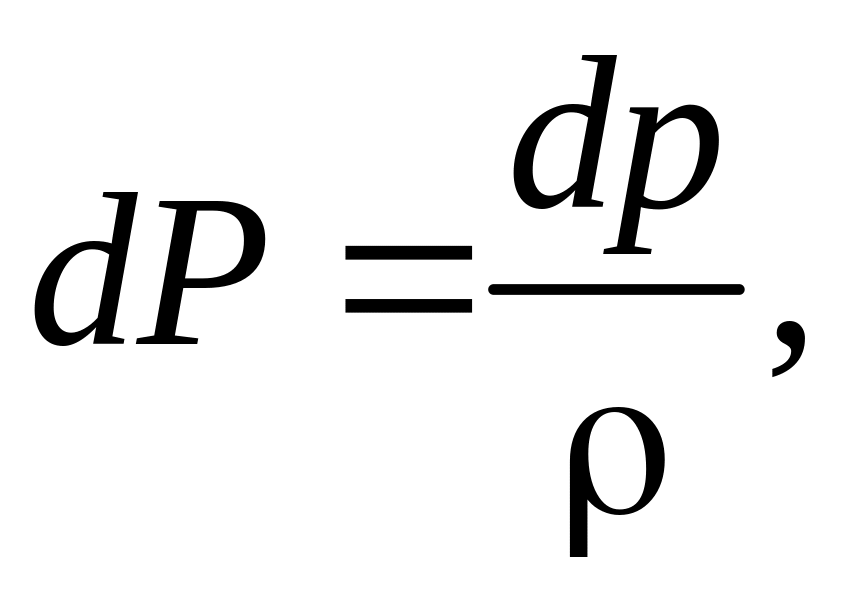Введем в рассмотрение такое понятие, как баротропность. Баротропным называется движение, при котором плотность есть функция только давления p. Будем считать, что баротропность имеет место во всем пространстве, занятом жидкостью. Тогда зависимость плотности от давления можно описать функцией давления . Следовательно, и отсюда .

В системе уравнений (3.25) произведем замены с помощью функции давления. Умножив каждое из уравнений на соответствующее приращение (dx, dy, dz)

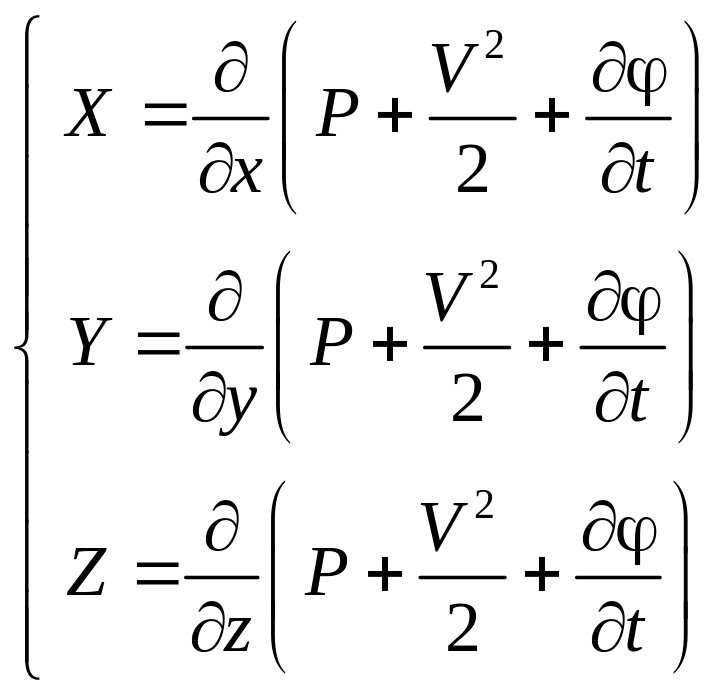
после их сложения получим следующее:

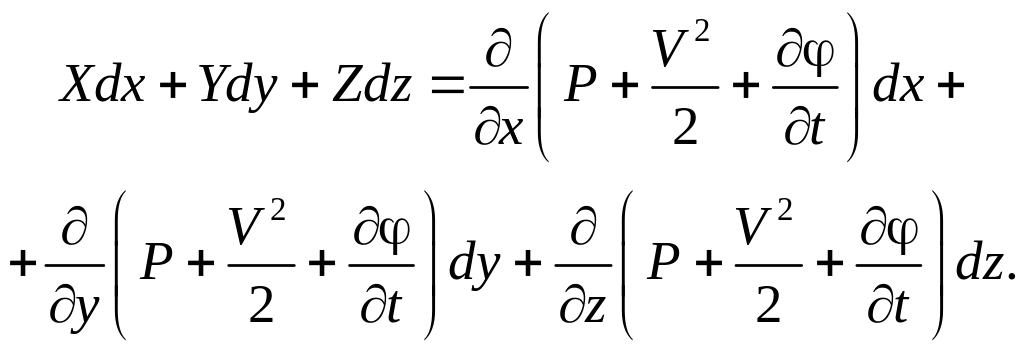(3.26)

Выражение в скобках 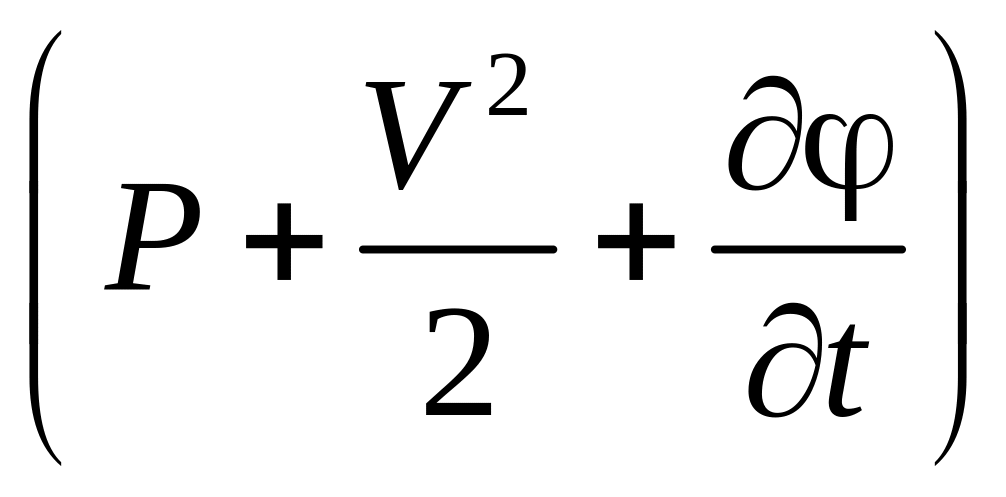в правой части уравнения является функцией и t, но, считая, что параметры течения на данном этапе не зависят от t, правую часть уравнения (3.26) можно считать полным дифференциалом некоторой функции

.

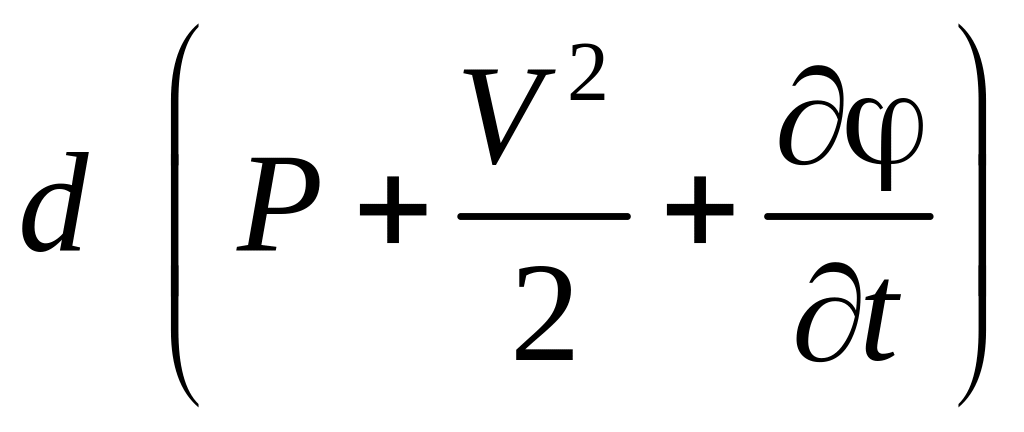Таким образом, уравнение (3.26) запишется в следующем виде: . Так как правая часть этого уравнения есть полный дифференциал, то и левая часть также является полным дифференциалом некоторой функции Ф:

.

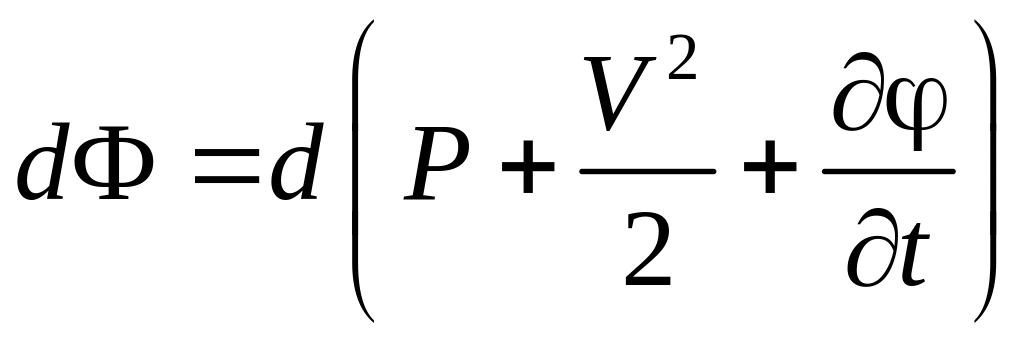После интегрирования получим 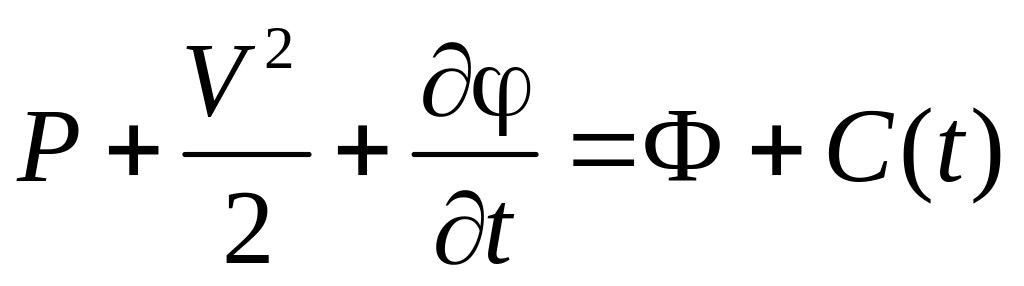, где C(t) – произвольная функция интегрирования, зависящая от t. Таким образом, мы восстанавливаем зависимость параметров течения от времени. С учетом выражения для функции давления получаем

т. е. интеграл Лагранжа для потенциального неустановившегося движения сжимаемой среды.

Для несжимаемой среды и интеграл Лагранжа для несжимаемой жидкости запишется следующим образом:

.

При установившемся движении сжимаемой жидкости вместо произвольной функции имеем постоянную интегрирования, и интеграл Лагранжа примет вид интеграла Эйлера–Бернулли:

,

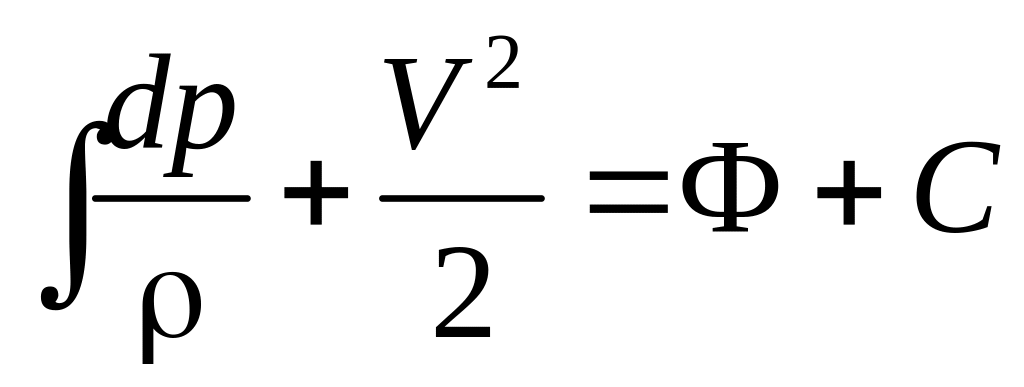где для всей массы движущегося газа.

Произвольное установившееся движение сжимаемой

жидкости (интеграл Бернулли)

При установившемся движении траектории и линии тока совпадают, и параметры течения являются функциями только координат. Считая движение баротропным, т. е. , уравнения Эйлера запишем в виде

, , .

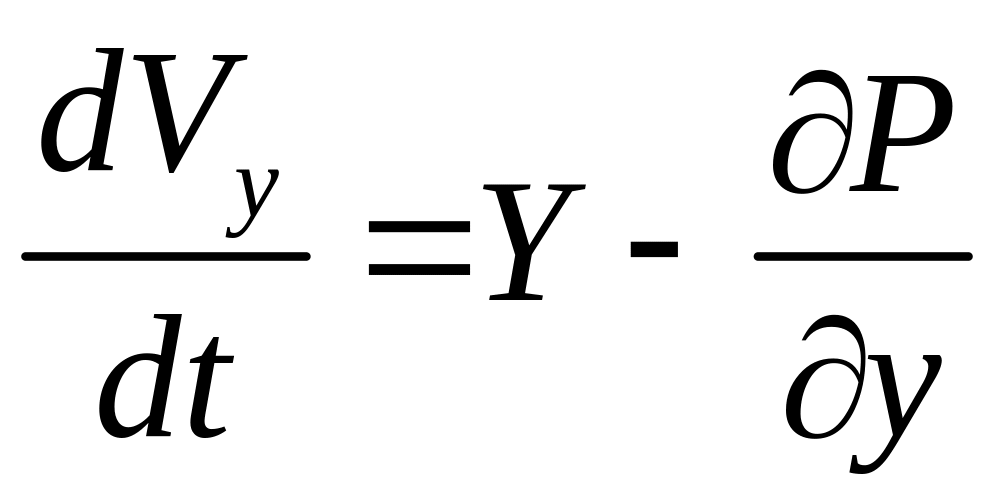После умножения каждого уравнения на соответствующее приращение , , и их суммирования получаем

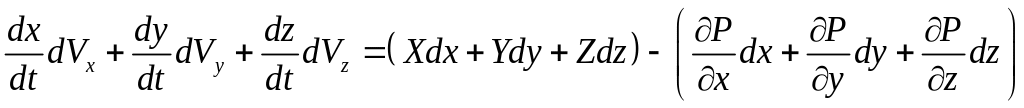. (3.27)

Так как на линии тока , и , левая часть уравнения (3.27) представляет собой полный дифференциал 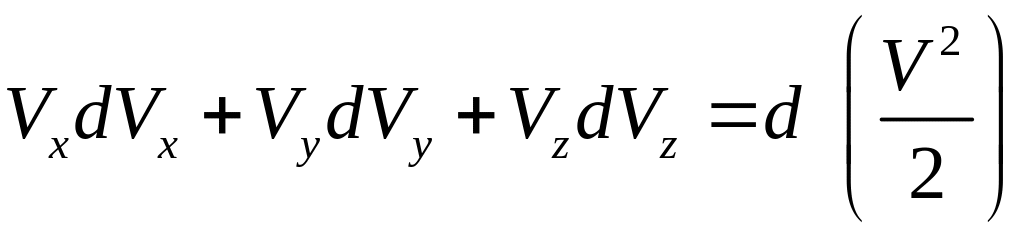. Следовательно, и правая часть уравнения (3.27) должна быть суммой полных дифференциалов:

и .

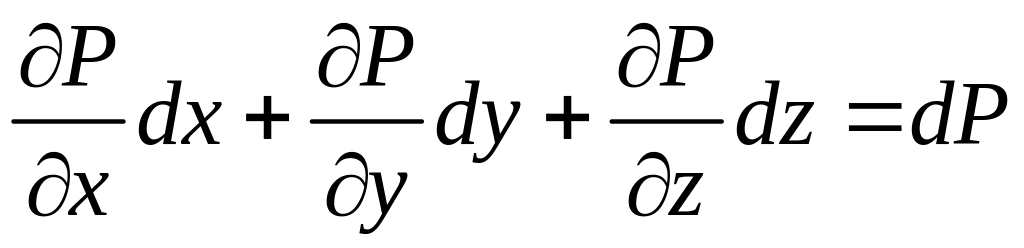Тогда уравнение (3.27) можно переписать в виде

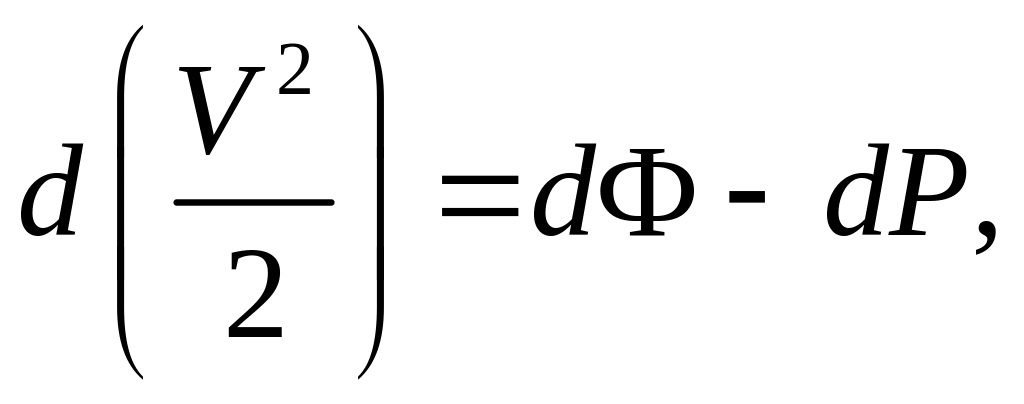или 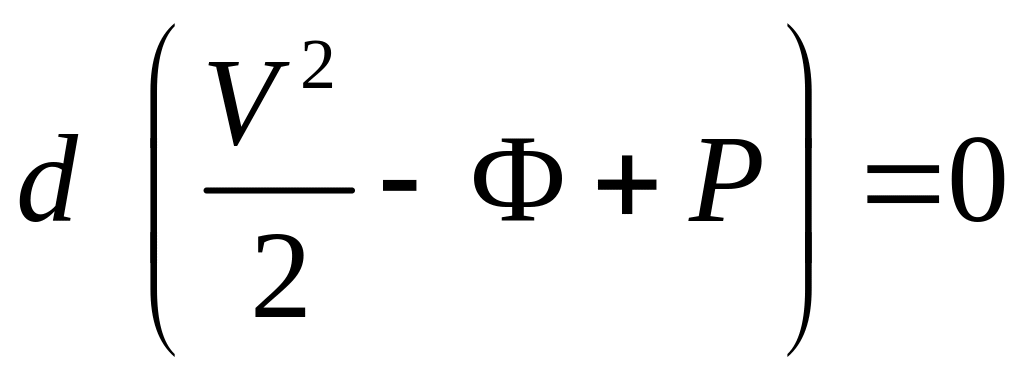. (3.28)

Взяв неопределенный интеграл от выражения (3.28), получим . С учетом выражения для функции давления

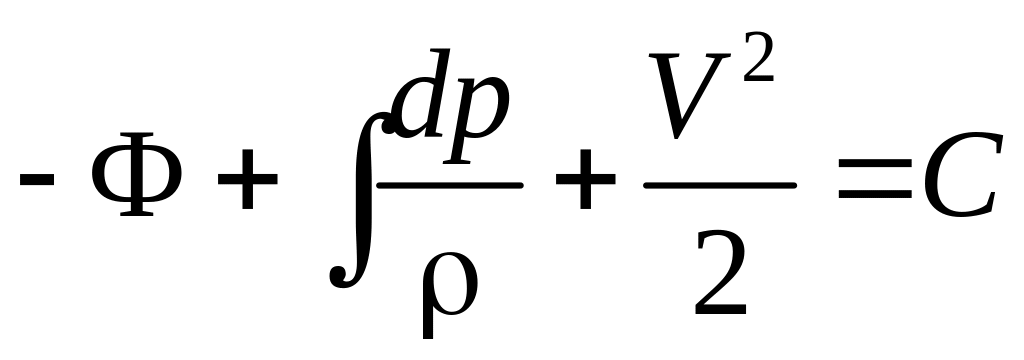. (3.29)

Полученное выражение есть интеграл уравнений Эйлера для установившегося движения сжимаемого газа, который носит название интеграла Бернулли. Интеграл Бернулли (3.29) тождественен по записи интегралу Эйлера–Бернулли. Однако разница здесь существенна и заключается в том, что произвольная постоянная в интеграле Бернулли (3.29) есть постоянная только вдоль линии тока.

Для несжимаемой жидкости и уравнение (3.29) перепишется в упрощенном виде: 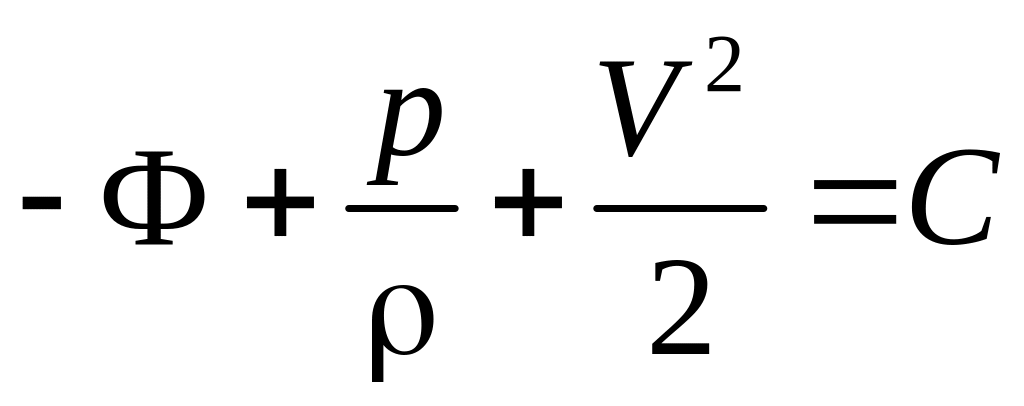. Пренебрегая массовыми силами (для газа), получаем уравнение Бернулли в виде

. (3.30)

Уравнение Бернулли (3.30) показывает, что при установившемся движении несжимаемой жидкости полный напор вдоль линии тока остается неизменным.

Для сжимаемого газа (без учета массовых сил) уравнение (3.29) имеет вид 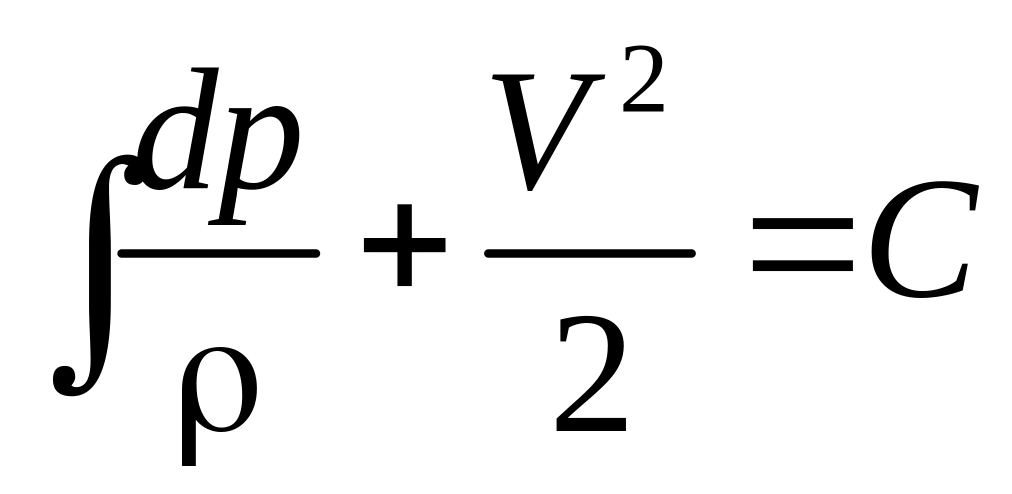. Для изоэнтропического течения 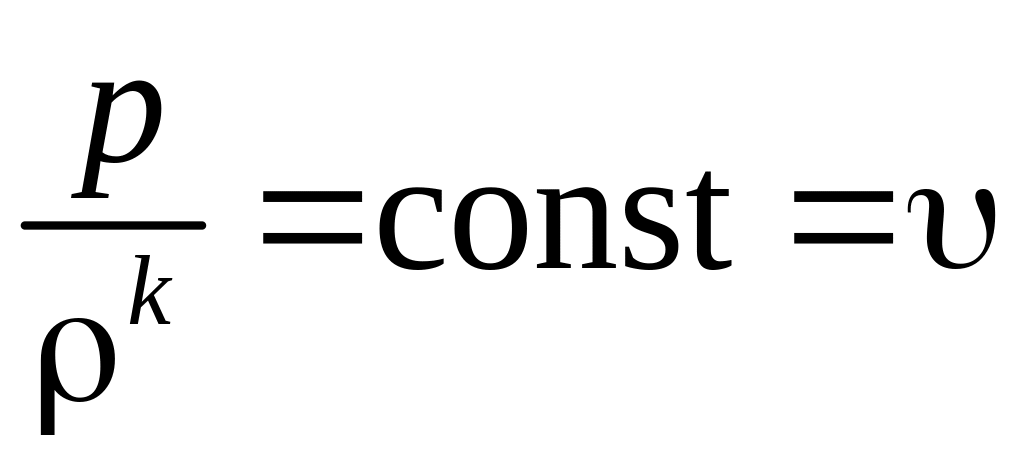. Отсюда , и дифференциал , а 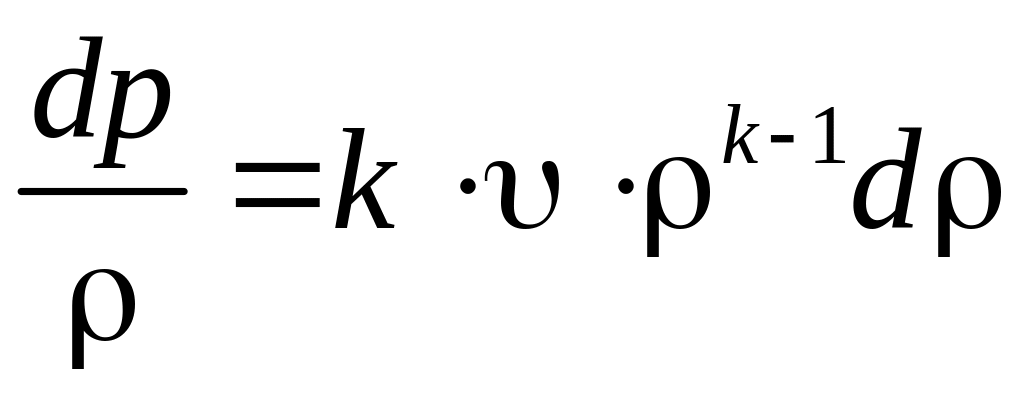. Поэтому

.

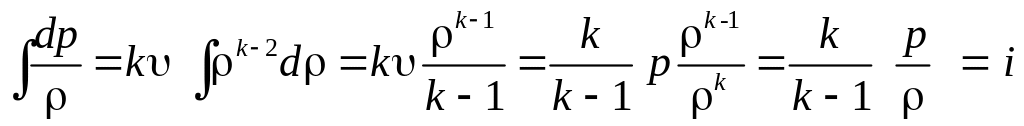Уравнение Бернулли для сжимаемого газа будет иметь вид

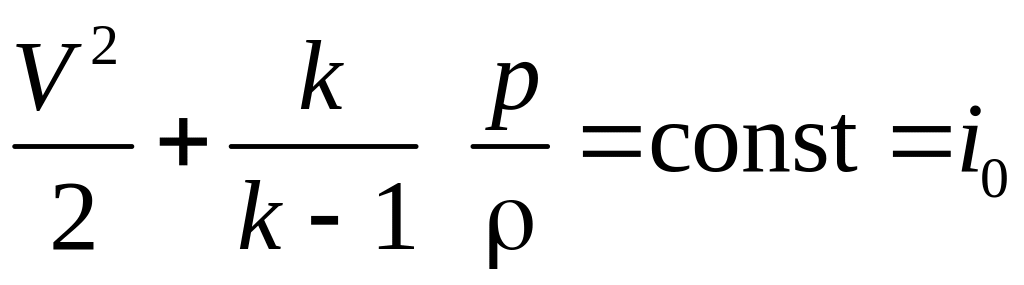, (3.31)

где – полная энтальпия, включающая энтальпию и кинетическую энергию единицы массы движущегося газа. Уравнение Бернулли есть уравнение энергии для изоэнтропического течения сжимаемого (или несжимаемого) газа.

Выражения для полной энтальпии можно записать через параметры заторможенного газа: 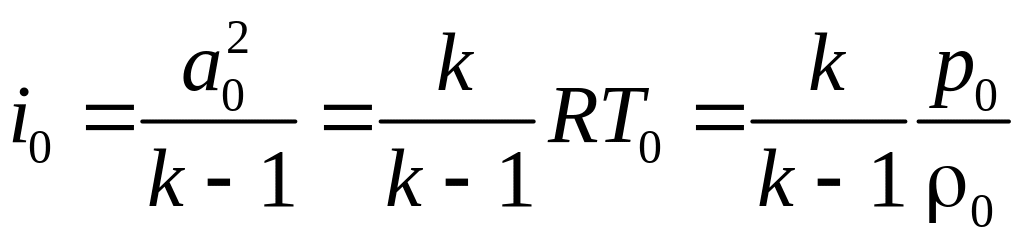. Другие формы представления энтальпии будут приведены далее.

Сравнивая интегралы Лагранжа и Бернулли, можно заметить, что интеграл Лагранжа в некотором смысле более общий, так как годится и для неустановившихся движений. Однако он менее общий в том смысле, что требует безвихревого движения и полной баротропности во всем пространстве движущейся жидкости.