Метод итераций
Способ итераций дает возможность получить последовательность приближенных значений, сходящихся к точному решению системы.
Рассмотрим систему из n линейных уравнений с n неизвестными:
(8)
Разрешим первое уравнение относительно x1, второе относительно x2 и т.д. Тогда систему (3.8) можно переписать в виде:
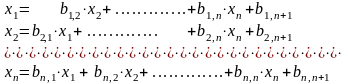(9)
где
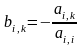(i=1,...,n,
k=1,..., n+1)
Правые части системы (3.9) являются функциями переменных x1, x2,..., xn. Обозначив правы части уравнений через Li(x1, x2, ...., xn) , систему (3.9) можно представить в виде:
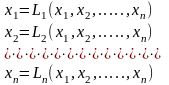(10)
Итерации начинаются с задания начального приближенного решения x01, x02, ... , x0n , которое может быть получено из физических или других разумных соображений. Чем ближе исходное приближение к решению, тем меньше итераций необходимо для его получения.
Для заданных начальных приближений x01, x02, ... , x0n после подстановки этих значений в правые части системы (3.10) получим первые приближения
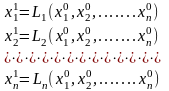(11)
Полученные первые приближения могут быть таким же образом использованы для получения 2-х, 3-их и т.д., так что для любого m можно получить m-ое приближение xm1, xm2, ... , xmn.
Итерации проводятся до получения решения с требуемой точностью, которая не должна превышать заданной погрешности вычислений, т.е. окончание итерационного процесса происходит при выполнении следующего неравенства:
,
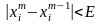при i=1,2,…n,
где Е – заданная точность решения.
Естественно возникает вопрос об условиях, выполнение которых обеспечивает сходимость полученных приближений к истинному решению системы. Достаточное условие сходимости, т.е. возможности решения СЛАУ методом итераций, формулируется следующим образом.
Для того чтобы итерационный процесс сходился, достаточно, чтобы в любой строке сумма отношений коэффициентов системы к диагональным коэффициентам, взятым из той же строки была строго меньше единицы.
Математически это определение может быть выражено следующим образом:
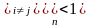
Или, что то же самое,
,
т.е. можно сказать, что в любой строке исходной матрицы на главной диагонали должен находиться коэффициент, по абсолютному значению превосходящий сумму модулей остальных коэффициентов.
На первом этапе решения СЛАУ система приводится к виду (10) , после чего происходит проверка условия сходимости итерационного процесса к решению системы. Для этого необходимо выбрать максимальные значения коэффициентов ai,i и провести проверку условия на сходимость итерационного процесса. После этого задаются начальные приближения, обычно для этого используется столбец свободных членов, и проводится расчет по формуле (11), которую можно представить в виде
,
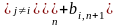до достижения окончательного решения. Здесь используется два вектора переменных: с предыдущими значениями X0 и с последующими значениями X1. В конце каждой итерации производится переприсваивание значений из последующих в предыдущие.
Метод Зейделя
Метод Зейделя является модификацией метода итераций. СЛАУ задается в виде (3.8) и приводится к виду (3.10). Отличие от метода итераций заключается в вычислительной процедуре нахождения приближения на i+1 итерации. В отличии от метода простых итераций , где для отыскания i+1 приближения используется i - ое приближение неизвестных xij , в методе Зейделя используются уже вычисленные i+1 значения x . Рекуррентные соотношения используемые в методе Зейделя представляются следующим образом:
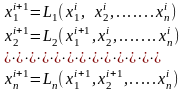(12)
Условия сходимости метода Зейделя может быть сформулировано следующим образом:
Для того чтобы итерационный процесс сходился, достаточно, чтобы сумма абсолютных значений элементов каждой строки (исключая диагональный) была меньше абсолютного значения диагонального элемента соответствующей строки.
Математически это определение может быть выражено следующим образом
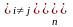
На первом этапе решения СЛАУ система приводится к виду (10), после чего происходит проверка условия сходимости итерационного процесса к решению системы. Для этого необходимо выбрать максимальные значения коэффициентов ai,i и провести проверку условия на сходимость итерационного процесса. После этого задаются начальные приближения, обычно для этого используется столбец свободных членов, и проводится расчет по формуле (12) до достижения окончательного решения.
Сравнение методов по эффективности
Количество
итераций в методе Гаусса при одинаковой
размерности матриц стационарно и корни
уравнения вычисляются настолько точно,
насколько позволяют ресурсы ЭВМ. Еще
один плюс метода в том, что метод работает
со всеми матрицами, у которых определитель
отличен от нуля. При отсутствии на
главной диагонали нулей количество
итераций приблизительно равно
,
не считая двух проверок на нулевые
элементы главной диагонали, занимающие
максимум 2n
в начале метода и после преобразования
в диагональную матрицу. Так же в случае
появления на диагонали нулей нам
потребуется процедура преобразования,
занимающая максимум
действий. При более точных расчетах для
матрицы 3*3 количество действий будет
составлять в лучшем случае 25, в худшем
52.
Метод
итераций, вообще говоря, применим для
частных случаев, когда модуль элемента
на ГД больше суммы модулей всех остальных
элементов. Кроме того значения корней
вычисляются с приближением. Проведем
анализ эффективности метода итераций
для матрицы 3
3.
Очевидно, что при увеличении размерности
время вычисления корней так же будет
увеличиваться.
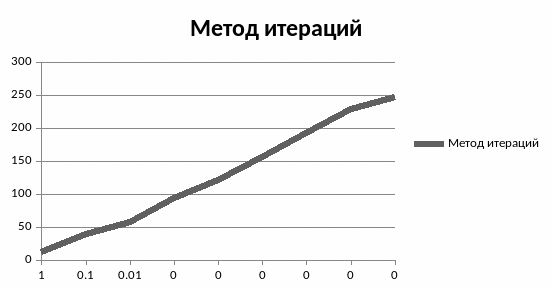
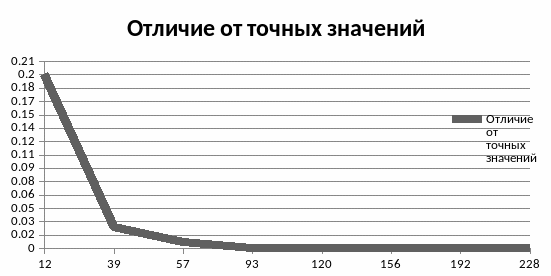
Как видно из
графиков, метод итераций значительно
уступает по скорости методу Гаусса,
начиная с точности 0,01. .при этом разница
вычисленных значений и точных
.
Так что если требуется найти значение
меньшей точности, метод итераций вполне
подойдет. Но для его сходимости необходимо
выполнение условия
Описание алгоритма решения задачи
Для решения задачи введены следующие пользовательские функции:
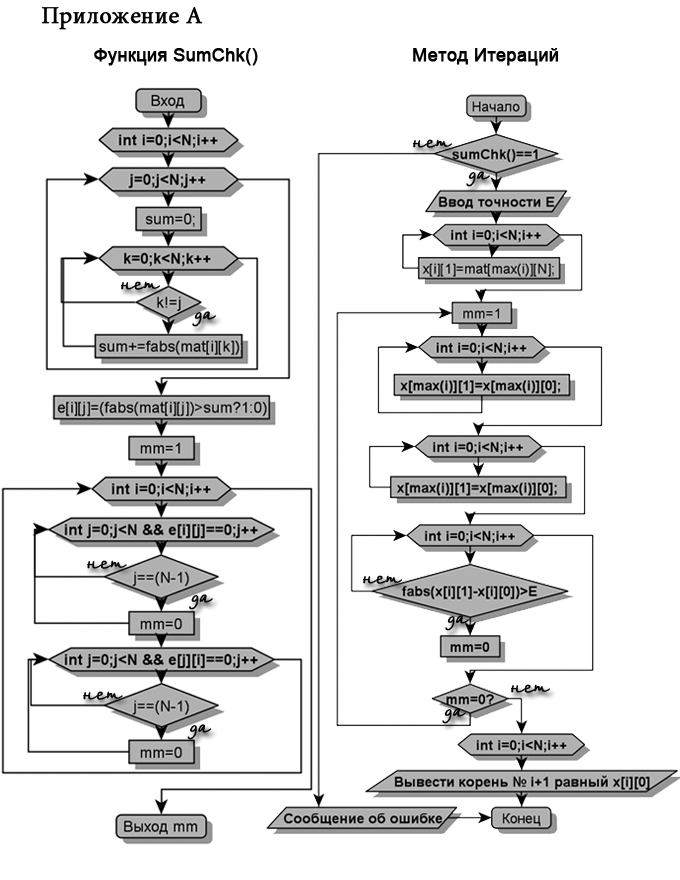
Нахождение максимального по абсолютному значению элемента строки. Используется для метода итераций, где по определению вычисляемый корень должен иметь максимальный коэффициент. Поиск максимального элемента производится через цикл, где производится сравнение значений элементов матриц с переменной, изначально равной нулю. В случае, если переменная меньше модуля текущего значения, переменной присваивается это значение, а так же запоминается номер данного элемента. По окончанию цикла функция возвращает номер максимального элемента.
Для приведения уравнения к виду, приемлемому для метода Гаусса введена функция обмена строк местами через промежуточную переменную.
Так же введена функция проверки нулевых значений на главной диагонали. Цикл со счетчиком и условием, что текущий элемент не равен нулю, пробегает диагональные значения. Если цикл был выполнен полностью, счетчик равен размерности матрицы, в этом случае функция возвращает 1, иначе 0
Функция проверки сходимости метода итераций для данных коэффициентов действует следующим образом: инициализируется булевой массив, который в случае, если модуль текущего элемент больше суммы модуля остальных элементов строки ставит 1 в ту же позицию булевого массива, иначе 0. Далее необходимо и достаточно проверить булевой массив на наличие нулевых строк и столбцов. Если таковых нет, метод сходится.
Так же нам необходима функция, вычисляющая выраженный корень. Так как максимальный элемент не обязательно должен находиться на диагонали, на входе в функцию необходимо задать номер столбца и строки.
В основном блоке программа считывает из файла размерность матрицы, считывает расширенную матрицу и сразу же выводит исходные значения в файл. Далее поступает запрос на выбор метода подсчета корней.
В методе Гаусса сначала идет проверка на наличие нулевых столбцов и строк, при наличии таковых определитель матрицы будет равен нулю, следовательно СЛАУ нельзя решить методом Гаусса. В противном случае стартует цикл, работающий до тех пор, пока элементы на диагонали перестанут быть равными нулю. В теле цикла осуществляется обмен между строками по следующему принципу: Если в текущей строке найдет диагональный элемент, ищем такую строку, чтобы при обмене с ней мы избавились от нуля на диагонали. Далее матрица по вышеописанному методу приводится к треугольной. Покажем, что произведение диагональных элементов треугольной матрицы есть определитель.
Пусть дана треугольная матрица А:
Разложим матрицу по первому столбцу. Первый столбец имеет единственный ненулевой элемент, соответственно все остальные слагаемые занулятся. Найдем алгебраическое дополнение первого элемента, а это определитель матрицы, полученной путем вычеркивания строки и столбца, на которых стоит данный элемент. То есть
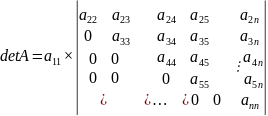
Раскладывая
новую матрицу по левому столбцу мы
увидим ту же картину. В конечном итоге
мы получим произведение
,
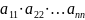которое и будет являться определителем
треугольной матрицы. Поэтому, если на
главной диагонали стоит хотя бы один
ноль, определитель равен нулю и решить
его методом Гаусса нельзя, более того,
любые разрешенные преобразования будут
бесполезны. Если определитель нулю не
равен, то методом обратной подстановки
программа находит все корни и выдает
их в файл.
Метод итераций начинается с вызова функции проверки на сходимость. Если проверка прошла успешно, одному из векторов присваиваются значения свободных элементов. После этого стартует цикл с условием, что булевая переменная равна 0. В теле этого цикла три цикла со счетчиком, первый из них приравнивает первый вектор ко второму, второй цикл вычисляет новые значения вектора, третий сравнивает первый вектор со вторым и в случае, если хотя бы одна разность значений оказалась меньше точности, приравнивает булевую переменную к нулю. Как уже говорилось ранее, в каждой строке выражается не диагональный элемент, а тот, у которого модуль больше суммы модулей остальных. В конце метода программа выводит решение в файл.
Руководство программиста
Программный код приложения разрабатывался на языке СИ.
В программе использованы следующие пользовательские функции:
int max(номер строки)
Возвращает номер элемента строки, модуль кото которого модуль больше суммы модулей остальных
void swtch(номер строки а, номер строки b)
меняет местами строку а со строкой b
bool chk()
Если на диагонали матрицы есть нули, возвращает 0, иначе 1
bool sumChk()
Проверяет метод итераций на сходимость
float L(номер строки, номер элемента)
Вычисляет выраженный х с заданным номером по второму вектору.
Основные моменты алгоритма приведены на блок-схеме в приложении А.
Листинг программы приведен в приложении В.
Пример входного и выходного файла в приложении С.
Руководство пользователя
После запуска
программа запросит метод решения СЛАУ.
Во входном файле matrix.txt
в первой строке должна быть указана
размерность матрицы, а налее записана
расширенная матрица размерностью
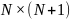. Результат вычисления корней записывается
в файл roots.txt
Вывод: В ходе лабораторной работы были изучены некоторыми численные методы решения систем линейных уравнений, которые были реализованы программно на языке СИ.
Приложение В
#include <stdio.h>
#include <conio.h>
#include <math.h>
#define maxN 7
float mat[maxN][maxN+1], x[maxN][2];
int N;
int max(int a)
{
int i1;
float m1=0;
for(int i=0;i<N;i++)
if(fabs(mat[a][i])>m1)
{
m1=fabs(mat[a][i]);
i1=i;
}
return i1;
}
void swtch(int a, int b)
{
float t;
for(int i=0;i<=N;i++)
{
t=mat[a][i];
mat[a][i]=mat[b][i];
mat[b][i]=t;
}
}
bool chk()
{
int i;
for(i=0;i<N && mat[i][i]!=0;i++);
if (i==N)
return 1;
else
return 0;
}
bool sumChk()
{
bool e[maxN][maxN];
for (int i=0;i<N;i++)
for (int j=0;j<N;j++)
{
float sum=0;
for (int k=0;k<N;k++)
{
if (k!=j)
sum+=fabs(mat[i][k]);
}
e[i][j]=(fabs(mat[i][j])>sum?1:0);
}
bool mm=1;
for (int i=0;i<N;i++)
{
for(int j=0;j<N && e[i][j]==0;j++)
if (j==(N-1))
mm=0;
for(int j=0;j<N && e[j][i]==0;j++)
if (j==(N-1))
mm=0;
}
return mm;
}
float L(int a,int b)
{
float y=0;
for(int i=0;i<N;i++)
if(i!=b)
y-=mat[a][i]*x[i][1]/mat[a][b];
y+=mat[a][N]/mat[a][b];
return y;
}
void main()
{
FILE *P;
char w;
bool mm=1;
P=fopen("matrix.txt","r");
fscanf(P,"%d", &N);
for (int i=0;i<N;i++)
for (int j=0;j<=N;j++)
fscanf(P,"%f",&mat[i][j]);
fclose(P);
P=fopen("roots.txt","w");
for (int i=0;i<N;i++)
{
for (int j=0;j<=N;j++)
fprintf(P,"%0.5f ", mat[i][j]);
fprintf(P,"\n");
}
fprintf(P,"\n");
do
{
printf("Choose way of roots calculation: iteration method(I) or Gauss method(G)\n");
scanf(" %c",&w);
}
while(w!='i' && w!='g' && w!='I' && w!='G');
if(w=='G' || w=='g')
{
for (int i=0;i<N;i++)
{
for(int j=0;j<N && mat[i][j]==0;j++)
if (j==(N-1))
mm=0;
for(int j=0;j<N && mat[j][i]==0;j++)
if (j==(N-1))
mm=0;
}
if (mm==0)
{
fprintf(P,"Cannot get roots because determinant is 0");
printf("Cannot get roots because determinant is 0\n");
}
else
{
while(chk()==0)
{
for(int k=0;k<N;k++)
if (mat[k][k]==0)
for(int j=0;j<N;j++)
if (mat[j][k]!=0) {swtch(j,k); break;}
}
for (int k=0;k<N-1;k++)
for (int i=k+1;i<N;i++)
for (int j=N;j>=k;j--)
mat[i][j]-=mat[i][k]/mat[k][k]*mat[k][j];
if (chk()==0)
{
printf("Cannot get roots because determinant is 0");
fprintf(P,"Cannot get roots because determinant is 0");
}
else
{
for(int i=N-1;i>=0;i--)
{
float sum=0;
for(int j=i+1;j<N;j++)
sum+=mat[j][N]*mat[i][j];
mat[i][3]=(mat[i][N]-sum)/mat[i][i];
}
fprintf(P,"Gauss method \n \n");
for(int i=0;i<N;i++)
fprintf(P,"x%d=%f \n",i+1,mat[i][N]);
}
}
}
else
{
float E;
if (sumChk()==1)
{
printf("Input accuracy (E)");
scanf("%f",&E);
for(int i=0;i<N;i++)
x[i][1]=mat[max(i)][N];
do
{
mm=1;
for(int i=0;i<N;i++)
{
x[max(i)][1]=x[max(i)][0];
}
for(int i=0;i<N;i++)
{
x[max(i)][0]=L(i,max(i));
}
for(int i=0;i<N;i++)
if (fabs(x[i][1]-x[i][0])>E)
mm=0;
}
while(mm==0);
fprintf(P,"Iteration method \n \n");
for(int i=0;i<N;i++)
fprintf(P,"x%d=%f \n",i+1,x[i][0]);}
else
{
fprintf(P,"Cannot get roots with method of iterations, try to use Gauss metod");
printf("Cannot get roots with method of iterations, try to use Gauss metod \n");
}
}
printf("You may check roots in file ROOTS.TXT");
fclose(P);
getch();
}
Приложение С
Входной файл Matrix.txt с точностью итерации 0.001:
3
4 2 -9 2
5 1 -3 3
-1 3 0 1
Выходной файл roots.txt:
4.00000 2.00000 -9.00000 2.00000
5.00000 1.00000 -3.00000 3.00000
-1.00000 3.00000 0.00000 1.00000
Iteration method
x1=0.588137
x2=0.529350
x3=0.156755
Gauss method
x1=0.588235
x2=0.529412
x3=0.156863