5.2. Метод Фурье для уравнения колебаний

Рассмотрим общую схему метода разделения переменных (Фурье) на примере краевой задачи для неоднородного уравнения колебаний [3].

Сформулируем краевую задачу для одномерного уравнения колебаний

, (5.18)

, (5.19)

. (5.20)

Задача состоит в отыскании функции , удовлетворяющей уравнению (5.18) и условиям (5.19), (5.20) в области - с границей .

Решим методом Фурье задачу (5.18) – (5.20). Будем искать нетривиальные решения в виде , Подставив предполагаемую форму решения в уравнение (5.18) и разделив переменные, получим

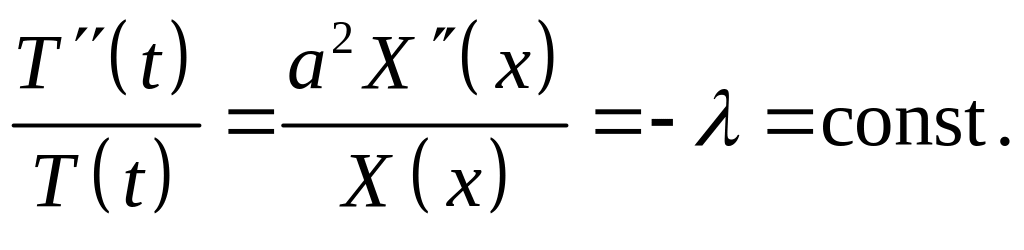
Поэтому функции и должны быть определены как решения дифференциальных уравнений

(5.21)

(5.22)

Граничные условия (5.20) дают:

.

Откуда заключаем, что функция должна удовлетворять дополнительным условиям

. (5.23)

Итак, мы приходим к задаче о собственных значениях дифференциального оператора, так называемой задаче Штурма-Лиувилля: найти те значения параметра , при которых существуют ненулевые решения граничной задачи (5.21), (5.23) [3].

Рассмотрим различные случаи, когда или .

1. При 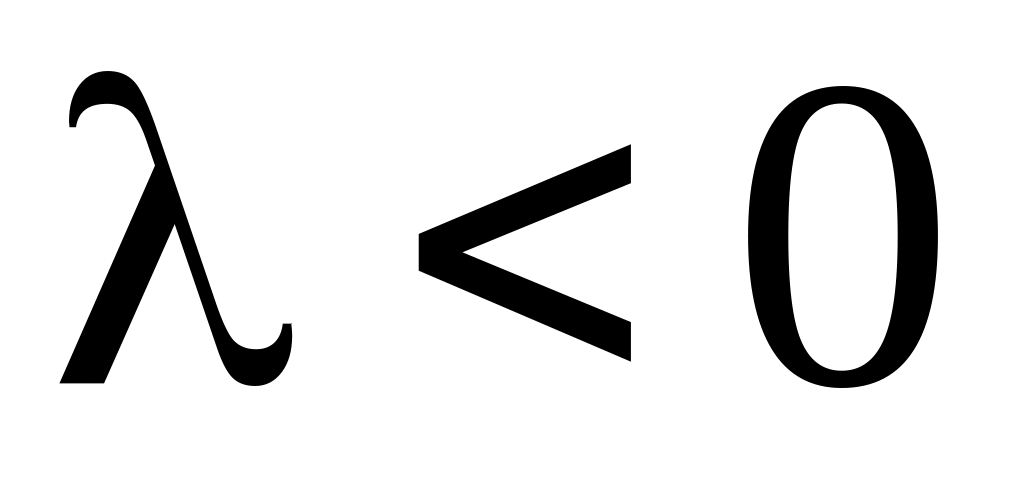общее решение ОДУ (5.21)

.

Граничные условия (5.23) дают

, так как , т.е. вспомогательная задача не имеет нетривиальных решений.

2. При 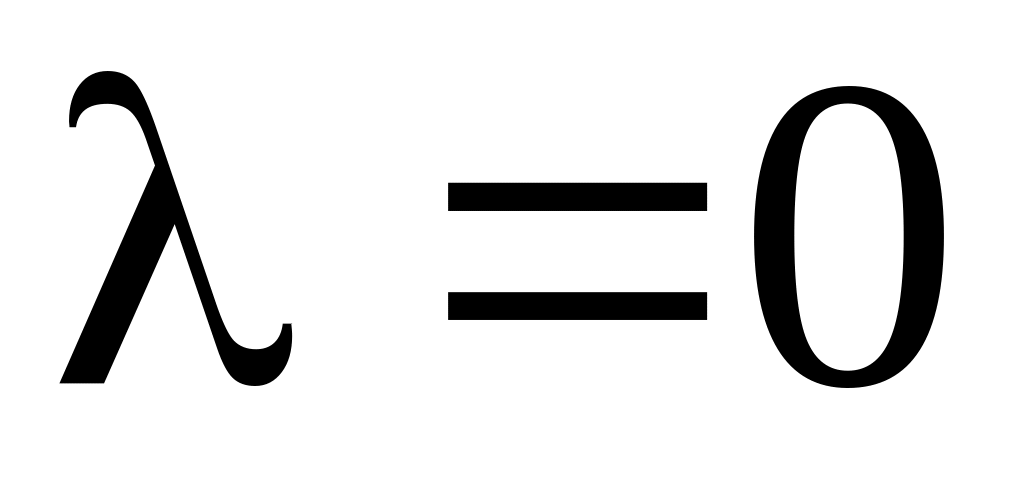общее решение ОДУ (5.21)

.

Граничные условия (5.23) дают

.

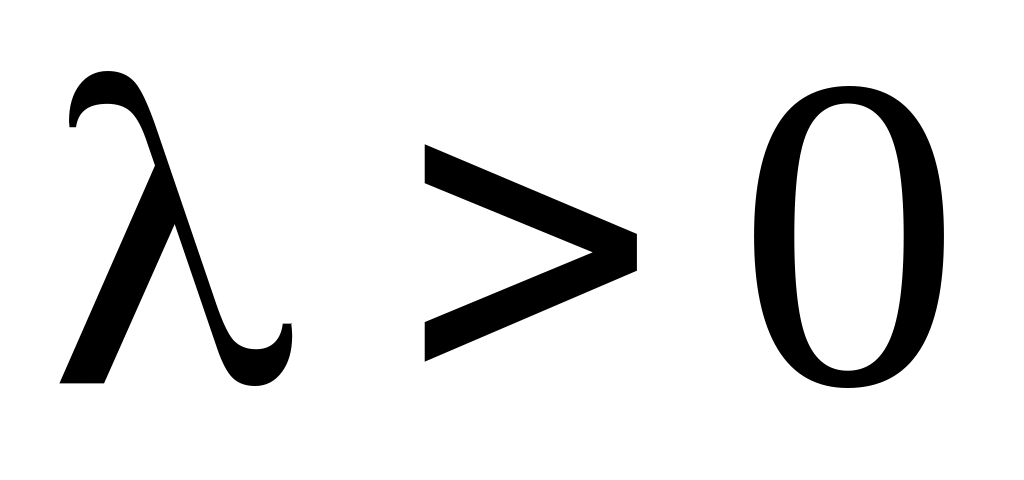3. При общее решение ОДУ (5.21) может быть записано в виде

.

Граничные условия (5.23) дают

.

Так как , то и поэтому или .

Таким образом, нетривиальные решения задачи (5.21), (5.23) возможны при собственных значениях

,

соответствующие собственные функции

.

Эта задача имеет счетное множество собственных функций и собственных значений , причем все . Кроме того, все собственные функции попарно ортогональны между собой и их можно нормировать, т.е. считать ортонормированными и систему - полной [4].

Примечание 1. Например, в качестве нормы ||.|| - может быть выбрана норма в классе функций, интегрируемых с квадратом, т.е.

Ортонормируемость системы функции в метрическом пространстве с выбранной нормой понимается как равенство нулю скалярного произведения , при всех и для любого n.

Для отыскания функций построим последовательность решений задач Коши

, (5.24)

(5.25)

где

. (5.26)

Тогда

. (5.27)

Решение задачи (5.18) – (5.20) запишется в виде

. (5.28)

Замечание 5.1.1. Для решения общей первой краевой задачи уравнения колебаний (5.7), (5.11), (5.12) ее можно привести к краевой задаче с однородными граничными условиями. Для этого построим функцию для которой выполняются граничные условия (5.12). Например, можно взять функцию, линейную относительно переменной :

.

Условия (5.12) дают

.

Следовательно

.

Теперь введем новую неизвестную функцию , полагая, что

.

Подставляя далее в (5.7), (5.11), (5.12) получаем краевую задачу для определения :

;

;

,

которая аналогична задаче (5.18)—(5.20).

Примечание 2. Для обеспечения сходимости ряда решений (5.28) и рядов, получаемых двукратным почленным дифференцированием этого ряда по и , установим ограничения на функции и .

Теорема 5.1. [1] Если , кроме того имеет третью, а - вторую кусочно-непрерывную производную на и выполняются условия согласования . Тогда сумма ряда (5.28) является классическим решением задачи (5.18) – (5.20).

Вообще говоря, условия теоремы 5.1 могут быть ослаблены. В этом случае ряд (5.28) является так называемым обобщенным решением краевой задачи [4]. Тогда сходимость ряда решений и его производных следует понимать в смысле сходимости в среднем или слабой сходимости.

Решения задач о свободных колебаниях ограниченной струны или стержня с однородными граничными условиями второго или третьего рода могут быть построены в виде функциональных рядов аналогичной структуры, отличающихся лишь решениями соответствующих вспомогательных задач Штурма-Лиувилля.