Практическое занятие № 6

Тема занятия: Численные методы решения уравнений в частных производных на координатных сетках

6.1. Введение в разностные методы

При решении краевых задач, возникающих на практике аналитические методы решения трудно применимы. Одним из приближенных численных методов решения дифференциальных уравнений в частных производных является метод сеток. Идея метода заключается в следующем. Для простоты, ограничимся случаем только функции двух переменных, и будем полагать, что решение уравнения ищется на квадратной области единичного размера (этого можно добиться, нормируя и обезразмеривая переменные задачи). Разобьем область сеткой. Шаг сетки по оси x и по оси y, вообще говоря, может быть разный. По определению частная производная равна

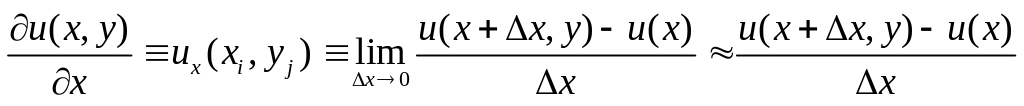. _(6.1)

Если рассматривать функцию только в узлах сетки, то частную производную можно записать (аппроксимировать) в форме

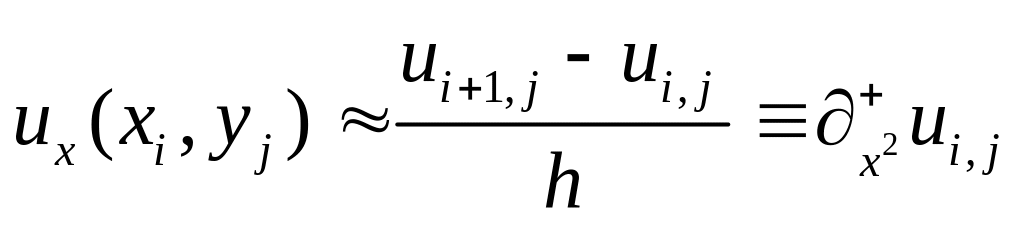, (6.2)

где узел соответствует точке .

Полученное выражение называется правой конечной разностью и имеет специальное обозначение. Название связано с тем, что для вычисления производной в точке используются значение функции в этой точке и точке, лежащей правее. Очевидно, что сходное выражение можно было бы получить, используя точку, лежащую слева.

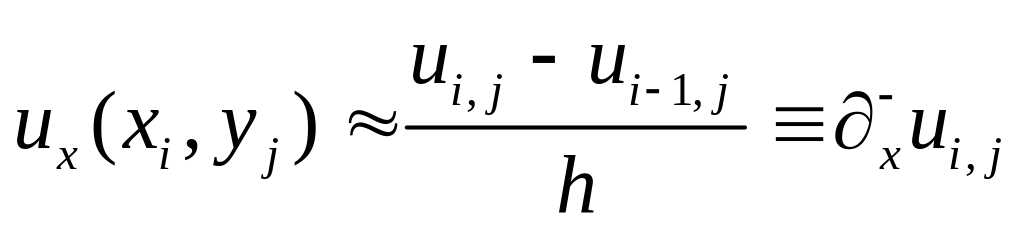. (6.3)

Такое выражение называется левой конечной разностью. Можно записать центральную конечную разность, найдя среднее арифметическое этих выражений. Введенные конечные разности называются разностными производными первого порядка.

Теперь получим выражения для вторых производных:

. (6.4)

В данном случае для нахождения производной мы использовали симметричные точки. Однако, очевидно, можно было бы использовать точки с несимметричным расположением.

6.2. Разностные уравнения, явная и неявная схемы

1. В качестве начального примера рассмотрим решение краевой задачи для волнового уравнения (уравнения гиперболического типа).

, (6.5)

, (6.6)

. (6.7)

Уравнение колебаний математической струны с заданными начальными смещениями и скоростями всех точек и произвольными законами на концах.

Составим разностную схему, соответствующую задаче (6.5) — (6.7). Для этого введем сеточную область. Выберем на временном интервале узловые точки

, (6.8)

г де - шаг по времени. Аналогично выберем координатные узлы , где - шаг по длине, n=0..N. Тогда на плоскости получится прямоугольная сетка (рис.6.1.). Прямую будем называть временным слоем или просто -слоем. Значения разностной функции в узлах сетки обозначим

, ( 6.9)

т.е. первый нижний индекс относится к пространственной координате, а второй к временному слою. Аппроксимируя производные разностной производной , разностной производной , получим уравнение в конечных разностях

. (6.10)

на следующей разностной явной схеме (см. рис.6.2.)

Рис.6.2.

Полученное уравнение позволяет выразить значение функции u в момент времени через значения функции в предыдущие моменты времени.

(6.11)

Зададим начальные и граничные условия (6.6), (6.7) на сетке

, , , (6.12)

Такая разностная схема называется явной, так как искомая величина получается в явном виде. Последние уравнения представляют собой систему линейных алгебраических уравнений, решение которой может быть найдено методом простой итерации.

Примечание. Заметим, что о том насколько хорошо разностный оператор аппроксимирует континуальный оператор можно судить по разности , где - разностный оператор, аппроксимирующий континуальный оператор , задающий уравнение, - точное решение, - проекция решения на сеточное пространство. Говорят, что разностное уравнение аппроксимирует уравнение с порядком или имеет место аппроксимация порядка , если . Таким образом, для того, чтобы имела место сходимость, т.е. решение разностного уравнения стремилось бы к точному решению уравнения при стремлении , необходимо, чтобы при стремилась к нулю разность где является решением разносного уравнения соответствующего данному т.е. . Однако для сходимости (корректности) одной аппроксимации разностным уравнением оказывается недостаточно. Разностная схема является устойчивой, если малое изменение правой части влечет за собой малое изменение решения. Другими словами, разностная схема называется устойчивой, если . Условие же аппроксимации тогда можно переписать в виде .

Итак, из аппроксимации и устойчивости следует сходимость. Это утверждение называется предельной теоремой Лакса. Условие устойчивости явных разностных схем (т. н. условно устойчивых) обеспечивается согласованием шагов сетки по осям, когда шаг по одной из осей выбирается в зависимости от величины шага по другой. В тоже время, условия согласования могут быть весьма обременительными из-за необходимости выбора слишком малого шага по одной из осей для получения устойчивого приближенного решения. Аппаратным методом решения этих проблем является применение других типов разностных схем (неявных), гарантирующих т. н. безусловную устойчивость. Для реализации неявной схемы часто используется специальный метод решения СЛАУ – метод прогонки. В последнее время актуализированными методами становятся универсальные многосеточные методы приближенного решения УЧП на структурированных сетках, в которых производится адаптация решаемых задач к численному методу, применяются несколько сеток на одном сеточном уровне для вычисления поправки, оригинальное построение грубых сеток, более эффективные типы дискретизаций исходной области.

Для устойчивости задачи (7.11 — 7.12) имеем условие согласования .

2. Еще один пример использования конечных разностей – уравнение теплопроводности (диффузии) (уравнение параболического типа).

На левом и правом торце стержня происходит тепловое взаимодействие с окружающей средой, и здесь необходимо задать граничные условия. Кроме того задана функция начальной температуры по всей длине стрежня.

Рассмотрим применение неявной схемы на примере уравнения теплопроводности вида

; (6.13)

; (6.14)

. (6.15)

Составим неявную разностную схему для этого уравнения

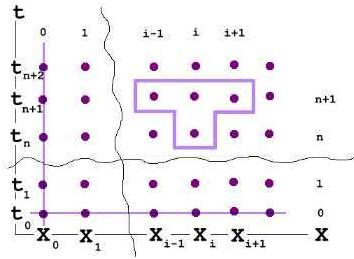
Рис.6.3.

Заменяем на сетке исходное дифференциальное уравнение его разностной аппроксимацией в соответствии с шаблоном (см. рис.6.3.).

. (6.16)

Здесь первый индекс соответствует пространственной, а второй – временной координате. В отличие от явной схемы, для вычисления в правой части уравнения используются значения функции на том же самом временном шаге. Вводя обозначение , уравнение (6.16) можно переписать в виде

.

или в матричной форме

.

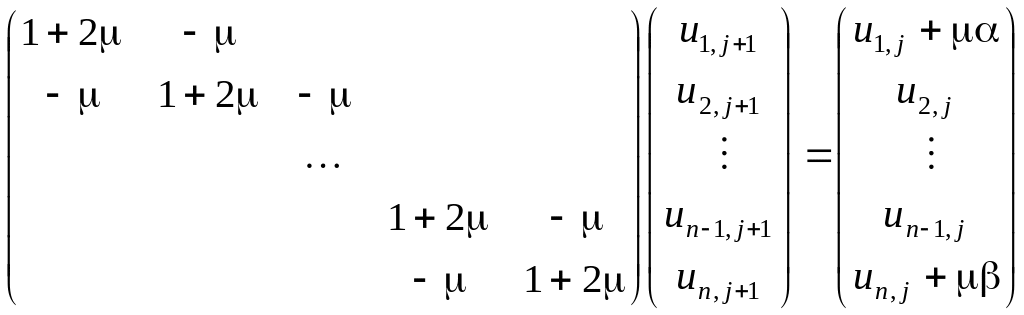Начальные и граничные условия (6.14), (6.15) на сетке имеют вид

,

Применять для таких разреженных матриц типовые алгоритмы (в частности, алгоритм Гаусса), например, встроенную функцию Lsolve Mathcad, расточительно. Для таких задач (а к ним приводит огромное количество неявных разностных схем для различных дифференциальных уравнений) применяется алгоритм прогонки.

3. Наконец, рассмотрим применение разностных методов к стационарным уравнениям эллиптического типа. Согласно идеям метода сеток уравнение Пуассона может быть записано в разностной форме при

помощи шаблона "крест" (рис.6.4.),

Рис. 6.4.

которая после приведения подобных слагаемых в разностных уравнениях имеет вид

. (6.17)

Разностная схема для уравнения Пуассона уже не может быть решена явно. Требуется решить систему линейных уравнений (6.17) т. н. методом релаксации. Для его запуска требуется задать начальное приближение к решению (нулевое приближение) и запустить итерационный процесс, уточняющий решение. Параметр численного алгоритма (число в пределах от 0 до 1) характеризует скорость сходимости итераций. Суть алгоритма релаксации сводится к тому, что в ходе итераций происходит проверка уравнений и соответствующая коррекция значений искомой функции в каждой точке. Если начальное приближение выбрано удачно, то можно надеяться, что алгоритм сойдется («срелаксирует») к правильному решению. Для решения стационарных уравнений Пуассона и Лапласа в Mathcad предназначена функция relax(a, b, c, d, e, f, u, rjac), реализующая метод релаксации. Поясним использование этой функции на простом примере. Фактически, эту функцию можно использовать для решения эллиптического уравнения общего вида

(6.18)

с граничными условиями

, (6.19)

которое может быть сведено к уравнению в конечных разностях (6.17).

В частности, для уравнения Пуассона (6.18) коэффициенты .

Метод релаксации заключается в следующем. Если нет источников (уравнение Лапласа), то значение функции в данном узле на текущем шаге (верхний индекс) определяется как среднее значение функции в ближайших узлах на предыдущем шаге k (шаблон разностной схемы имеет вид «крест»):

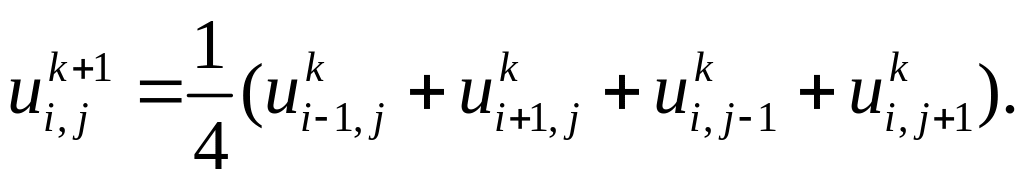(6.20)

При наличии источников разностная схема будет

(6.21)

Метод релаксации сходится достаточно медленно, так как фактически он использует разностную схему с максимально возможным для двумерного случая шагом .

В методе релаксации необходимо задать начальное приближение, то есть значения функции во всех узлах области, а так же граничные условия.