
Практическое занятие № 5
Тема занятия: Метод Фурье для линейных уравнений в частных производных второго порядка
5.1. Элементы общей теории уравнений в частных производных (учп)
Определение 5.1. Будем понимать под уравнением в частных производных второго порядка соотношение вида:
![]() (5.1)
(5.1)
Здесь
![]() ,
,
![]() ,
,![]() -
обозначения частных производных первого
и второго порядка функции
-
обозначения частных производных первого
и второго порядка функции
![]() по соответствующим переменным
по соответствующим переменным![]() .
.
Определение
5.2. Классическим решением
уравнения (5.1) назовем функцию
непрерывную и имеющую непрерывные
частные производные, входящие в (5.1) и
обращающую равенства (5.1) в тождество
относительно
![]() .
.
Определение
5.3. Если известная функция
![]() линейна относительно искомой функции
и ее производных, то уравнение (5.1)
называется линейным.
линейна относительно искомой функции
и ее производных, то уравнение (5.1)
называется линейным.
УЧП второго порядка с переменными коэффициентами
![]() ,
(5.2)
,
(5.2)
невырожденным линейным преобразованием
![]() (5.3)
(5.3)
приводятся к так называемому каноническому виду, в соответствии со знаком выражения, называемого дискриминантом
![]() .
.
Возможны следующие случаи:
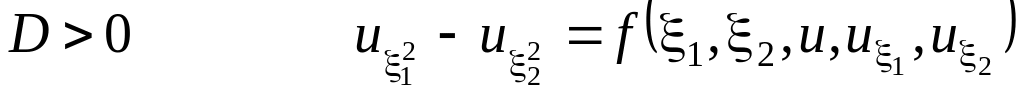 (5.4)
(5.4)
(5.4) – уравнение гиперболического типа.
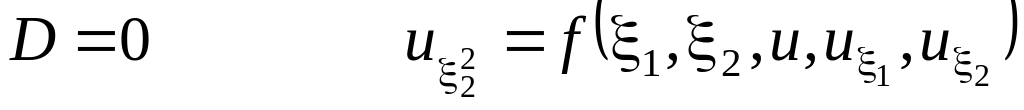 (6.5)
(6.5)
(5.5) – уравнение параболического типа.
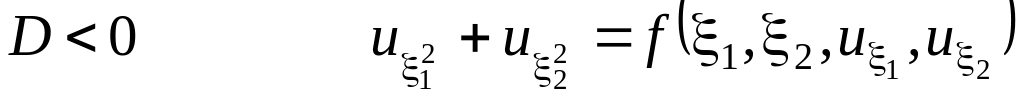 (5.6)
(5.6)
(5.6) – уравнение эллиптического типа.
В качестве примеров УЧП уравнений математической физики соответствующих типов приведем:
гиперболический тип
![]() - (5.7)
- (5.7)
уравнение малых поперечных колебаний математической струны или же малых продольных колебаний стержня [1]. В двумерном случае
![]() - (5.8)
- (5.8)
уравнение малых поперечных колебаний мембраны [1];
параболический тип
![]() - (5.9)
- (5.9)
уравнение теплопроводности или уравнение диффузии [1],
где
![]() -
-
![]() -мерный
оператор Лапласа;
-мерный
оператор Лапласа;
эллиптический тип
![]() - (5.10)
- (5.10)
уравнение Пуассона описывает установившиеся (стационарные) процессы колебаний или распространения тепла [1].
Еще один пример - уравнение Гельмгольца [1]
![]() .
.
Для корректной постановки задач о решении УЧП приведенных типов, рассмотрим два рода задач: задачи Коши и краевые задачи [2].
Формулировка задачи Коши: нужно
найти решение уравнения (5.7), (5.8) для
![]() (здесь
(здесь
![]() - ограниченная область с гладкой границей
- ограниченная область с гладкой границей
![]() )
при начальных условиях.
)
при начальных условиях.
 (5.11)
(5.11)
Формулировка краевой задачи: пусть
уравнения (5.7), (5.8) рассматриваются в
цилиндре
![]() (знак
(знак
![]() - обозначает декартово произведению
множеств). Нужно найти функцию
- обозначает декартово произведению
множеств). Нужно найти функцию
![]() ,
удовлетворяющую уравнениям (5.7) или
(5.8), начальным условиям (5.11) ,а также
одной из следующих групп краевых условий:
,
удовлетворяющую уравнениям (5.7) или
(5.8), начальным условиям (5.11) ,а также
одной из следующих групп краевых условий:
![]() (5.12)
(5.12)
![]() (5.13)
(5.13)
![]() (5.14)
(5.14)
![]() ,
(5.15)
,
(5.15)
![]() ,
(5.16)
,
(5.16)
![]() ,
(5.17)
,
(5.17)
где
![]() - боковая поверхность цилиндра
- боковая поверхность цилиндра
![]() ,
,
![]() - внешняя нормаль к
- внешняя нормаль к
![]() ,
,
![]() -
нормальная производная функции
-
нормальная производная функции
![]() .
.
Получим первую (5.7), (5.11), (5.12) или (5.8), (5.11), (5.15), вторую (5.7), (5.11), (5.13) или (5.8), (5.11), (5.16), и третью (5.7), (5.11), (5.14) или (5.8), (5.11), (5.17) - смешанную краевую задачу для УЧП.
Физически условия (5.11) соответствуют заданию начальных отклонений и начальных скоростей точек струны или мембраны. Краевые условия (5.12) означают, что концы струны движутся по заданному закону, (5.13) – по концам струны приложены определенные силы. (5.14) – на концах струны присутствуют и упругие силы.
Для уравнения (5.9) ставятся аналогичные
задачи, только в начальных условиях
(5.11) отсутствует производная по
![]() .
Для уравнения (5.10) задается только
краевое условие одного из трех видов
(5.15—5.17).
.
Для уравнения (5.10) задается только
краевое условие одного из трех видов
(5.15—5.17).
