
- •§1. Учет погрешностей вычислений.
- •§2. Оценка погрешностей результатов действий над приближенными значениями чисел. (Строгий учет погрешности)
- •§3. Приближенные вычисления без учета погрешностей.
- •§4. Связь между числом количества верных цифр и относительной погрешностью.
- •§5. Прямая задача теории погрешностей (функции от приближенных значений аргументов).
- •§6. Обратная задача теории погрешностей.
- •Принцип равных влияний
- •§7. Метод границ.
- •§8. Математические модели и численные методы.
- •§9. Понятие корректно поставленной и некорректно поставленной задач.
- •§10. Вспомогательные сведения из функционального анализа.
- •§11. Решение уравнений с одним неизвестным. Дихотомия.
- •§12. Метод простой итерации для решения алгебраических и трансцендентных уравнений.
- •По соседним приближениям
- •По невязке
- •§13. Метод Ньютона. Решение уравнений с одной переменной.
- •§14. Метод хорд. Метод секущих.
- •§15. Метод Гаусса решения систем уравнений.
- •§16. Метод квадратного корня.
- •Литература
§12. Метод простой итерации для решения алгебраических и трансцендентных уравнений.
ТЕОРЕМА 1. (Принцип Банаха сжимающихся отображений).
Пусть
R
– полное метрическое пространство.
Если
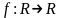 сжатие, то для него существует в R
единственная неподвижная точка, к
которой сходится итерационный процесс.
сжатие, то для него существует в R
единственная неподвижная точка, к
которой сходится итерационный процесс.
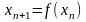 ,
где
,
где
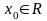 - произвольный.
- произвольный.
План доказательства.
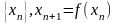 – фундаментальная
– фундаментальная
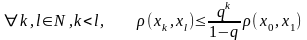 (*)
(*)
q – коэффициент сжатия
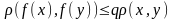 .
.
Т.к. R – полное метрическое пространство, то в нем всякая фундаментальная последовательность сходится.
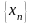 – сходится,
– сходится,
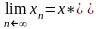 ,
причем
,
причем
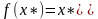 ,
т.е.
– неподвижная точка.
,
т.е.
– неподвижная точка.
– единственна.
ЧТД.
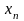 - последовательность
приближения к решению уравнения
- последовательность
приближения к решению уравнения

Метод – метод простой итерации.
Если
в (*)
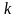 зафиксировать, а
зафиксировать, а
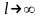 ,
то
,
то
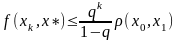 – оценка погрешности,
оценка скорости сходимости.
– оценка погрешности,
оценка скорости сходимости.
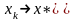 со скоростью
геометрической прогрессии.
со скоростью
геометрической прогрессии.
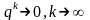 – линейная скорость
сходимости.
– линейная скорость
сходимости.
Метод простой итерации имеет линейную скорость сходимости.
Пусть
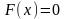 (2),
(2),
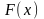 – вещественная функция.
– вещественная функция.
Необходимо
привести к виду
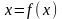 .
.
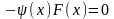 ,
,
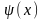 - знакопостоянная непрерывная функция.
- знакопостоянная непрерывная функция.
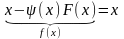
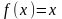
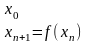
Условие сходимости для данного метода:
ТЕОРЕМА 2.
Пусть выполняются условия:
Функция – определена и непрерывна на отрезке
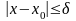 и на этом отрезке удовлетворяет условию
Липшица:
и на этом отрезке удовлетворяет условию
Липшица:
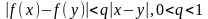 ;
;Для начального приближения
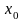 выполняется условие
выполняется условие
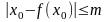 ;
;Числа
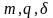 связаны условием
связаны условием
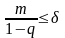 .
.
Тогда
уравнение
имеет единственное решение
в области
,
к которому сходится итерационный процесс
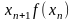 со скоростью сходимости
со скоростью сходимости
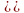 .
.
Теорема доказывается аналогично теореме Банаха с точностью до обозначений.
Замечание. Условие Липшица применять трудно, вместо него применяют другое условие:
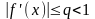 на отрезке
на отрезке
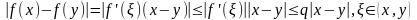 .
.
Метод итерация дает бесконечную последовательность приближений, поэтому используют следующие правила остановки:
По соседним приближениям
задается
уровень останова
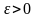 и момент останова n
задается формулой
и момент останова n
задается формулой
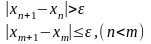
По невязке
задается уровень и момент останова n итерационной процедуры задается неравенствами
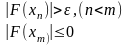
Метод простой итерации удобен в использовании, так как он легко программируется на ЭВМ.
Недостаток: невысокая скорость сходимости, т.е. линейная.
§13. Метод Ньютона. Решение уравнений с одной переменной.
Пусть
требуется решить уравнение
(1),
где функция
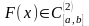 – дважды непрерывно-дифференцируема
на
;
– дважды непрерывно-дифференцируема
на
;
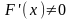 на
и
на
и
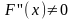 и
и
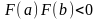 .
.
Из этих условий вытекает, что на функция имеет только один корень.
Прежде, чем использовать итерации, необходимо (1) привести к виду .
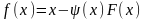 .
.
Функция
непрерывная в окрестности корня
уравнения (1). Следовательно, уравнение
(1) и уравнение
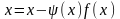 (2)
будут иметь один и тот же корень
.
(2)
будут иметь один и тот же корень
.
В
качестве
выберем
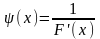 ,
тогда
,
тогда
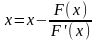 (3)
(3)
Выберем начальное приближение достаточно близкое к . Остальные приближения получаются по формуле:
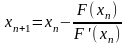 (4)
(4)
Метод, определенный (4), называется методом Ньютона.
Докажем, что метод Ньютона сходится и получим его оценку погрешности.
Если дано, что
,
где
|
|
|
|
|
Докажем, что (4) сходится.
Для
этого покажем, что отображение
– сжатие, где
 .
.
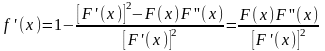 .
.
При получим
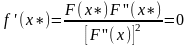 .
.
По
непрерывности функции
на
существует такая окрестность точки
,
что для
 ,
,
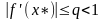 ,
а этом сжатие.
,
а этом сжатие.
Поэтому к отображению можно применить принцип сжатыхотображений.
Если
выбрать
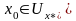 ,
то
будет сходиться к точному решению
уравнения (1)., т.е.
.
,
то
будет сходиться к точному решению
уравнения (1)., т.е.
.
Заметим,
что метод (4) будет сходиться, если
начальное приближение
будем выбирать из окрестности
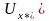
,
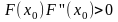 .
.
Докажем, что метод Ньютона сходится.
Определим скорость сходимости метода Ньютона. Для этого разложим в ряд Тейлора в точке .
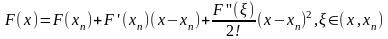 .
.
При
имеем
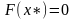 .
Поэтому
.
Поэтому
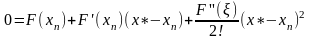
Выразим
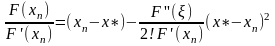 (5)
(5)
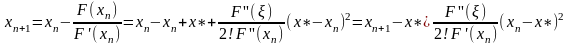 Обозначим
через
Обозначим
через
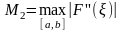 ,
,
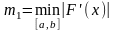
(6)
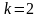 ,
скорость сходимости метода Ньютона
квадратичная,
,
скорость сходимости метода Ньютона
квадратичная,
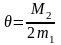 .
.
Потребуем, чтобы начальное условие выбиралось из условия
 (7)
(7)
Тогда из (6) получим
- оценка погрешности.
Метод Ньютона имеет квадратичную скорость сходимости. Это означает, что при переходе от одной итерации к другой количество верных знаков удваивается в последующем приближении.
Достоинство: высокая скорость сходимости, легко программируется на ЭВМ.
Недостатки: узкая область сходимости.
Если
будем решать операторное уравнение
,
то на каждом шаге необходимо находить
значение обратного оператора
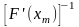 .
.
Геометрический смысл метода Ньютона.
П
 усть
требуется решить уравнение
и единственный корень этого уравнения
находится на
усть
требуется решить уравнение
и единственный корень этого уравнения
находится на
 .
.
В
точке
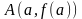 проведем касательную к графику функции
проведем касательную к графику функции
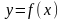 ,
уравнение касательной:
,
уравнение касательной:
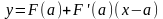 .
.
Если
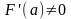 ,
то
,
то
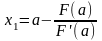 – первое приближение
к
уравнения (1) по методу Ньютона.
– первое приближение
к
уравнения (1) по методу Ньютона.
Возьмем
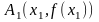 и проведем касательную в этой точке.
Получим
и проведем касательную в этой точке.
Получим
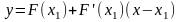 .
.
Если
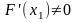 ,
то
,
то
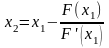 – второе приближение
к
уравнения (1) по методу Ньютона.
– второе приближение
к
уравнения (1) по методу Ньютона.
И так далее. Отсюда метод Ньютона называют методом касательных.

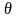 – символ Ландау:
– символ Ландау: