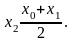§10. Вспомогательные сведения из функционального анализа.

Определение. Множество Х произвольных элементов называется метрическим пространством, если 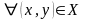ставится в соответствие число 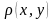, удовлетворяющее следующим условиям:

1. ;

2. ;

3. 

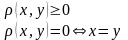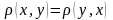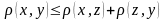
– расстояние между x и y.

1-3 – аксиомы метрики.

Говорят, что множество элементов 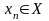- метрическое пространство сходится к , если

, .

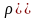
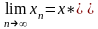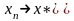Последовательность точек 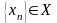называется сходящейся в себе (фундаментальной), если .

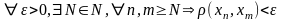Всякая сходящаяся последовательность является фундаментальной, обратное верно не всегда.

Определение. Метрическое пространство, в котором всякая фундаментальная последовательность сходится называется полным.

Пример. .

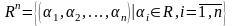Зададим различными способами расстояния:

1. кубическая метрика, m-метрика

;

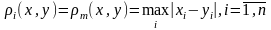2. сферическая метрика, 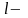метрика

;

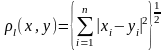3. октаэдрическая, s-метрика

.

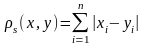Для всех выполняются аксиомы метрики и в каждой 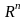– полное метрическое пространство.

Пусть X,Y – метрические пространства.

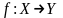называется оператором, заданным в X со значением в Y.

Если X=Y, то 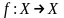– оператор, отображающий Х в себя (преобразование).

Если 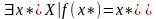, то 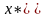– неподвижная точка при отображении .

Определение. Говорят, что отображение называется сжимающим (сжатием), если .

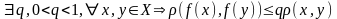§11. Решение уравнений с одним неизвестным. Дихотомия.

Пусть требуется решить уравнени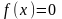е (1), где 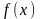– непрерывная функция.

Число 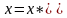называется корнем уравнения (1), если .

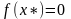Если функция определена и непрерывна на 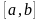и на концах отрезка принимает значения разных знаков, то на существует хотя бы один корень.

Отделить корень уравнения значит найти такой интервал, внутри которого находится один и только один корень данного уравнения.

Для отделения корней можно применить следующий признак:

Если на отрезке функция непрерывна и монотонна, и на концах отрезка принимает значения разных знаков, то на данном отрезке существует только один корень уравнения (1).

Достаточным условием монотонности функции на отрезке является сохранение знака производной.

Отделить корень можно и графически: нарисовать график и указать точки пересечения с осью Ох.

Совершенный метод отделения корней – метод Штурма.

Дихотомия (метод деления отрезка пополам).

1. Пусть

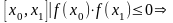существует хотя бы один корень на ;

2. 

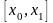Рассмотрим и 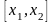. Из этих двух выберем тот, на концах которого функция принимает значения разных знаков и поделим его пополам и т.д.

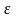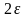Если нужно найти корень с точностью до , то мы продолжаем делить отрезок до тех пор, пока длина отрезка не станет меньше , тогда середина последнего отрезка дает значение корня с требуемой точностью.

Дихотомия проста и очень надежна: к простому корню она сходится всегда для любой непрерывной функции в том числе и недифференцируемой, при этом она устойчива к ошибкам округления. Скорость сходимости метода дихотомии не велика, т.е. за одну итерацию точность увеличивается вдвое.

Недостатки: прежде чем применить, необходимо найти отрезок, на концах которого функция принимает значения разных знаков. Если на этом отрезке несколько корней, то неизвестно к какому из них сходится дихотомия. Метод не применим к корням четной кратности.

Метод применим к корням нечетной кратности, но хуже устойчив к ошибкам округления. Метод не применим к системам уравнений.