4. Ортогональность и ортогональное дополнение

Элемент х называется ортогональным подпространству , если х ортогонален любому элементу В этом случае записывают .

Имеет место следующая весьма важная теорема.

Теорема 9. Если и L – некоторое подпространство гильбертова пространства H, то

(4),

где и Указанное разложение единственно.

Доказательство. Если , то, очевидно Предположим поэтому, что Пусть и {y_n} – последовательность из L такая, что при .

Пусть далее, h – любой элемент из L, отличный от нулевого вектора. Тогда y_n+ εh L для любого ε, и поэтому , т.е. .

Полагая

получаем, что , откуда или

(5).

При h = 0, неравенство (5) также очевидно выполняется. Из этого неравенства для любого следует

,

и полагая, в частности, получим

Поэтому последовательность {y_n} фундаментальна, а значит, в силу полноты H, сходится к некоторому вектору . Так как L замкнуто, то

Переходя к пределу в неравенстве (5), получаем, что , и так как h – любой элемент из подпространства L, то . Полагая , получаем требуемое равенство .

Докажем теперь единственность этого представления. Пусть , , где . Тогда и

, (6)

ибо , а . Но (6) означает, что . Следовательно, также . Теорема доказана.

Элемент y в разложении (4) называется проекцией вектора x на подпространство L. Из предыдущего видно, что совокупность M всех векторов, ортогональных подпространству L есть также подпространство, которое называется ортогональным дополнением к подпространству L и обозначается H - L; говорят также, что H есть ортогональная сумма подпространств L и M, и пишут H = LM. Можно, также, сказать, что элемент z предыдущего разложения есть проекция элемента x на подпространство M.

Теорема дает, таким образом, разложение на два взаимно дополнительных ортогональных подпространства.

Теорема 9. Для того чтобы линейное многообразие М было всюду плотно в Н, необходимо и достаточно, чтобы не существовало вектора, отличного от нулевого и ортогонального всем элементам многообразия М.

Необходимость. Прежде всего очевидно, что из следует . Но по условию и, следовательно, , в частности , откуда следует, что , и необходимость доказана.

Достаточность. Пусть М не всюду плотно в Н. Тогда и существует элемент . По предыдущей теореме имеем , где , , и так как , то ; что противоречит условию, и достаточность доказана.

5. Ряды Фурье в гильбертовом пространстве. Коэффициенты Фурье. Неравенство Бесселя и равенство Парсеваля. Полные и замкнутые ортонормированные системы

Пусть L – подпространство гильбертового пространства Н, порожденное ортонормальной системой и . Тогда, для любого существует, линейная комбинация , такая, что . Но

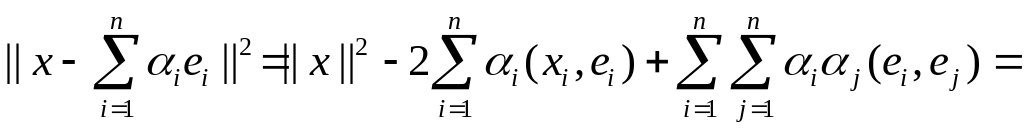
, где .

Числа с_i называются коэффициентами Фурье вектора x относительно ортонормальной системы . Из последнего равенства получаем

.

Отсюда следует, что норма разности принимает наименьшее значение, когда коэффициенты являются коэффициентами Фурье элемента относительно системы . В этом случае имеем

, (7)

и так как можно выбрать сколь угодно малым, то

Из формулы (7) следует также, что ряд сходится причём .

Пусть теперь x – любой элемент пространства H. Обозначим через z проекцию x на L; тогда , где и . Так как , , , то . Следовательно, для любого элемента x из H справедливо неравенство

,

где , . Это соотношение называется неравенством Бесселя.

Пусть в пространстве H дана ортонормальная система элементов . Если не существует элемента , отличного от нулевого и ортогонального всем элементам системы , то эта система называется полной. Ортонормальная система называется замкнутой, если подпространство L, порождаемое этой системой, совпадает с H. Ряд Фурье по замкнутой системе, построенной для любого , сходится к этому элементу и для любого имеет место равенство Парсеваля

Замкнутая ортонормальная система называется также ортонормальным базисом гильбертова пространства.

Если ортонормальная система полная, то она замкнутая. Поскольку, в этом случае не существует вектора отличного от нулевого и ортогонального линейному многообразию L, порождаемому системой. Но тогда в силу теоремы 9 и система замкнутая.

Обратно, замкнутая ортонормальная система полна, так как для такой системы

и если , т.е. , то , что означает полноту системы .

Примером полной ортонормальной системы является система тригонометрических функций

в пространстве .

Теорема 10. В любом сепарабельном гильбертовом пространстве существует полная ортонормальная система векторов.

Доказательство. Пусть – любое счётное всюду плотное множество в пространстве H, причём все , отличны от нулевого вектора. Полагаем

,

и пусть - одномерное пространство, порождённое элементом . Пусть – первый элемент множества G, не принадлежащий и - проекция на . Полагаем

.

Пусть - подпространство, порождённое элементами и , и - первый элемент множества G не принадлежащий . Пусть - проекция на . Полагаем

,

и т.д. Получаем ортонормальную систему и так как каждый элемент принадлежит некоторому в силу построения этих подпространств, то подпространство, определяемое системой совпадает с подпространством определяемой системой , т.е. с H. При этом система , очевидно счётная, в случае когда, H бесконечномерно, ибо если бы она содержала конечное число p векторов, то в H не существовало бы p + 1 линейно независимых векторов, что противоречит бесконечномерности H. Теорема доказана.

Задачи

1. Множество в линейном пространстве называется выпуклым множеством, если оно вместе с любым двумя точками содержит все точки

, , , ,

или, геометрически выражаясь, содержит отрезок, концами которого являются точки и . Доказать, что любой шар в линейном нормированном пространстве является выпуклым множеством.

2. Доказать, что неравенство треугольника в определении линейного нормированного пространства можно заменить условием выпуклости единичного шара.

3. На плоскости взято произвольное центрально-симметричное замкнутое выпуклое множество Q, у которого начало координат является внутренней точкой. Доказать, что существует норма, в которой Q является единичным шаром.

4. Доказать, что конечномерное подпространство нормированного пространства Е всегда замкнуто в Е.

5. Задает ли норму в пространстве R₁ функция (х) = |arctgx|?

6. Установить непосредственно эквивалентность следующих норм в - мерном линейном нормированном пространстве X:

,

.

Что будут представлять собой единичные шары и в пространстве с этими нормами.

7. Проверить аксиомы нормированного пространства для пространства матриц размера :

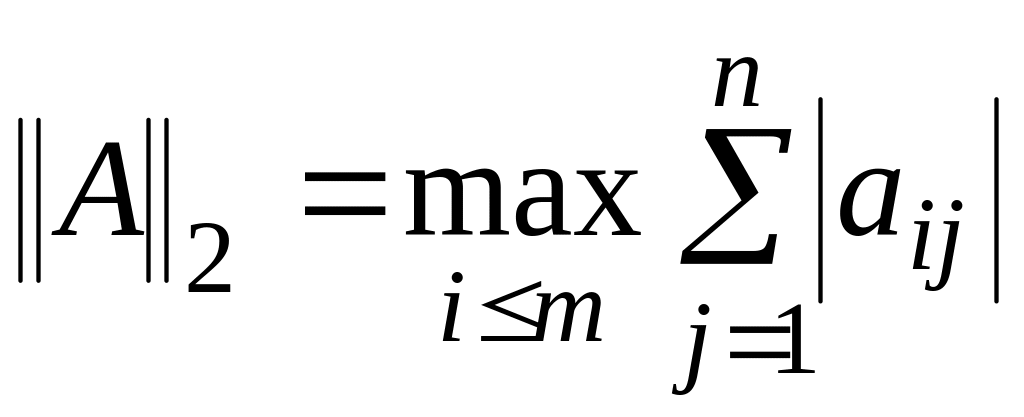а) , б) , в) .

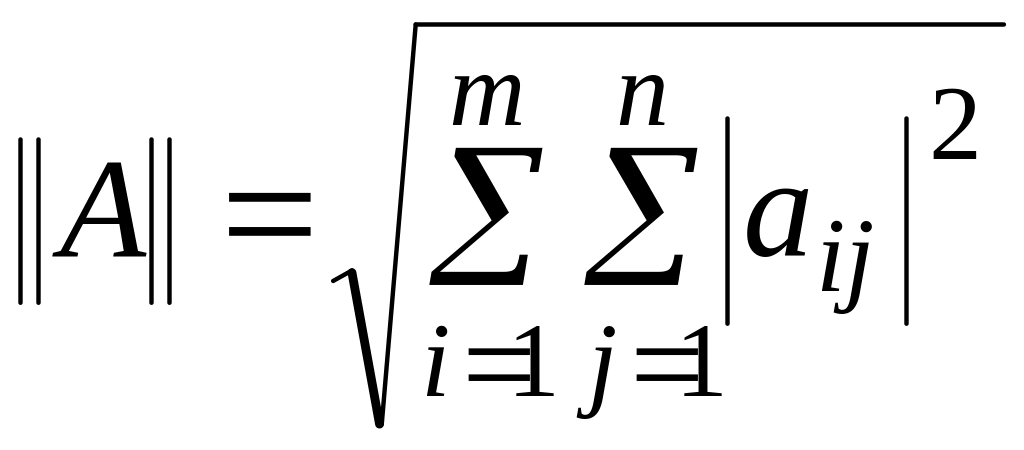8. Доказать, что пространство банахово в нормах предыдущего примера.

9. Доказать, что  (Использовать неравенство Минковского).

10. Является ли нормой в пространстве непрерывно-дифференцируе-мых функций C¹[a, b] на отрезке [a, b] следующие величины:

a)

b) |x(b) – x(a)| +

c) |x(a)| +

d)

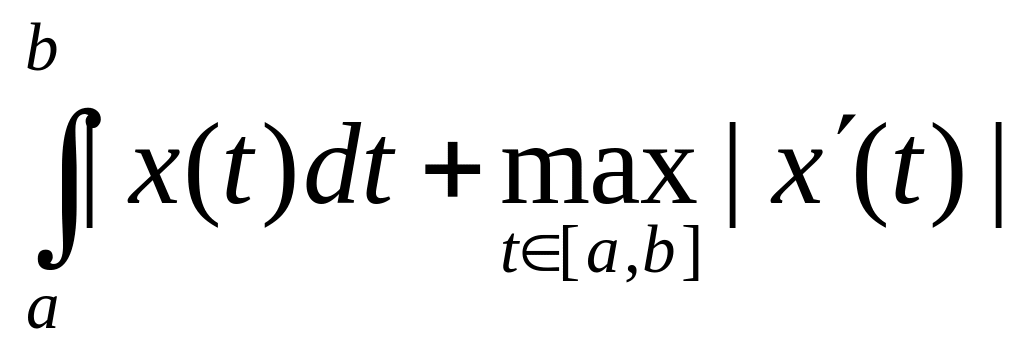
11. В множестве непрерывных функций, определённых на , каждая из которых равна нулю вне некоторого конечного интервала (своего для каждой функции), вводится норма . Будет ли пространство этих функций полно в метрике ? Если нет, то что будет пополнением этого пространства?

12. Является ли пространство C¹[a, b] банаховым по норме

.

13. Доказать, что пространство M[a, b] – ограниченных на отрезке [a, b] функций с нормой является банаховым.

10. Найти бесконечномерное линейное подпространство L  такое, что

11. Показать, что проекция вектора из гильбертова пространства H на подпространство есть элемент этого подпространства, находящийся на кратчайшем расстоянии от х, т.е.

для любого .

12. Известно, что в некотором нормированном пространстве Е для любой пары векторов х и у справедлива лемма о параллелограмме (т. е. ). Рассмотрим функцию

.

Доказать, что она удовлетворяет всем аксиомам скалярного произведения и .

13. В гильбертовом пространстве даны последовательности {x_n},{y_n} такие, что ||x_n||  1, ||y_n||  1 и (x_n, y_n)1. Докажите, что ||x_n  y_n||  0.

14. Докажите, что множество {x: ||x  a|| = ||x  b||} является выпуклым в гильбертовом пространстве. Верно ли это заключение для произвольного банахова пространства?

15. Пусть в банаховом пространстве Х множества А замкнутое, а B компактное. Докажите, что множество А+B замкнутое. При этом из замкнутости А и B не следует замкнутость А+B.

16. Докажите, что любое семейство замкнутых ограниченных выпуклых множеств в гильбертовом пространстве имеет непустое пересечение. Верно ли это для любого банахова пространства?

17. Пусть а[0, 1] и С_a={xС: x(а) = 0}. Докажите, что С_a подпространство С. Является ли оно всюду плотным? А если это множество рассматривать в пространстве L²?

18. Докажите, что множество функций из С, для которых , является бесконечномерным подпространством в С.

19. Пусть В₁ и В₂ – шары в нормированном пространстве с радиусами соответственно r₁ и r₂. Доказать, что если В₁  В₂, то r₁  r₂.