Лекция №2

Если есть система ортогональных функций в пр-ве Гилберта, то её можно разложить по базису.

Базис:

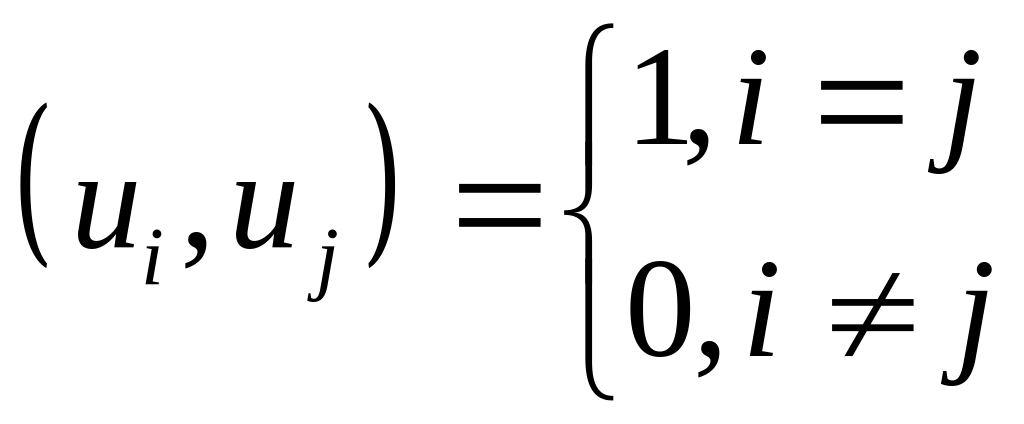
Обобщенный ряд Фурье

Классическое представление сигнала – ряд Фурье. Он определён для периодических функций ( u(t)=u(t+T) ):

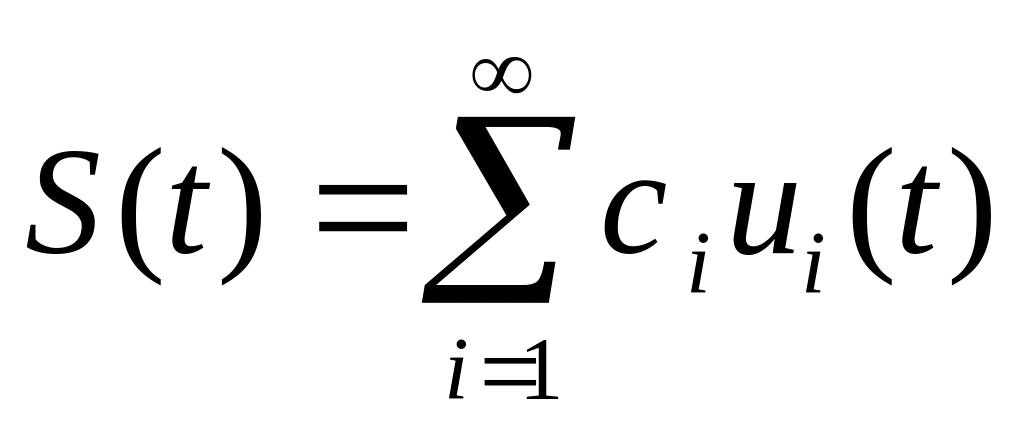
– базисные вектора (синусы, косинусы), - коэффициенты ряда Фурье.

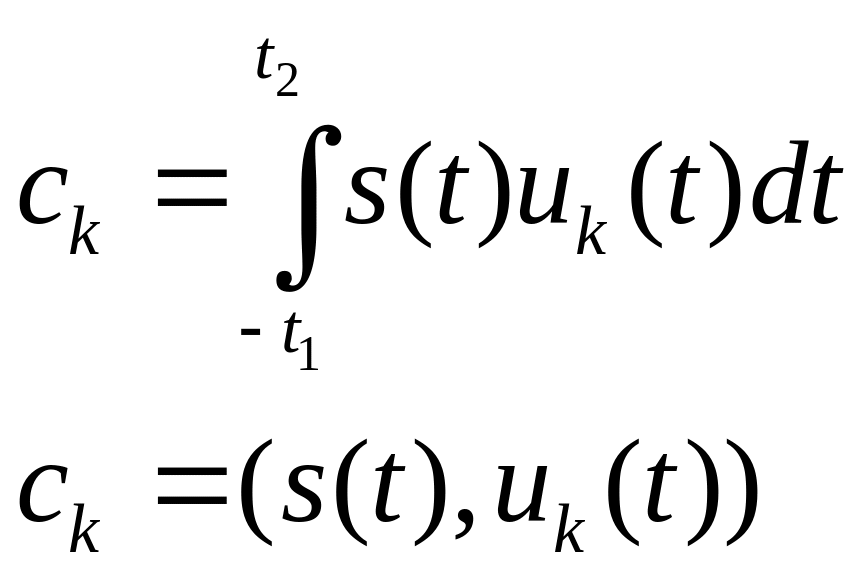
Ряд Фурье.

Если непрерывная функция времени периодическая, то ее можно разложить в ряд Фурье, т. е. представить в виде суммы sin и cos:

,

где а₀ – постоянная составляющая.

Для тригонометрического ряда Фурье с периодом 2π:

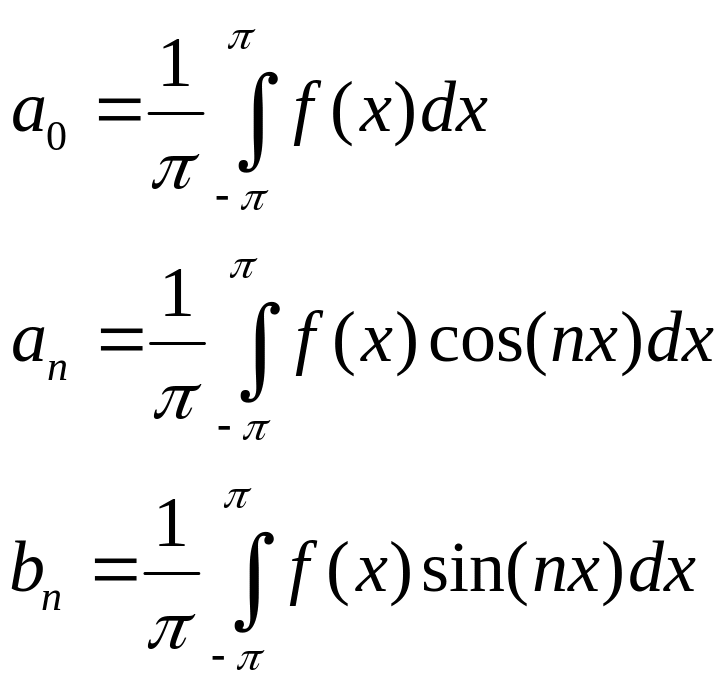
Если период T = 2l, то:

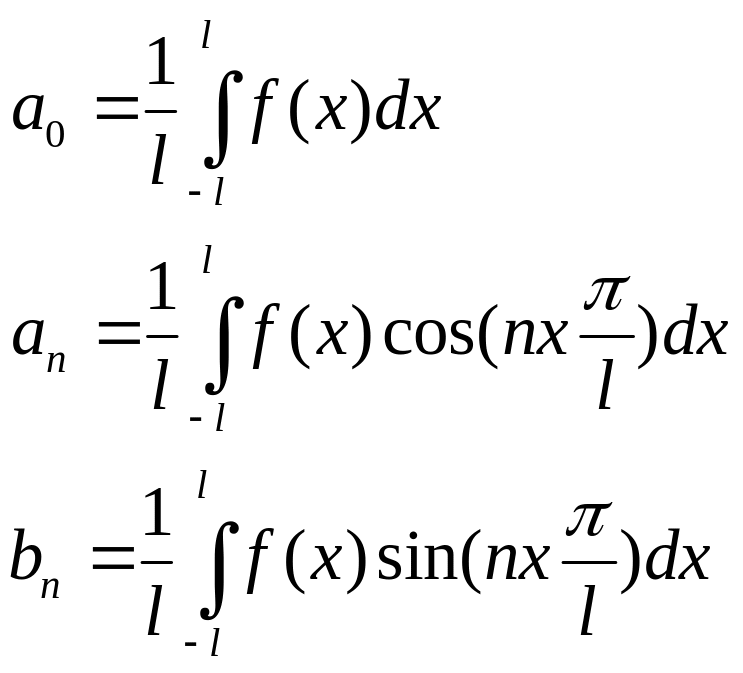
Любой сигнал имеет две абсолютно равноправные формы представления:

- в виде функции времени S(t) ( в пространстве времени t ≥ 0);

- в виде распределение сигнала по различным частотам S(f) (в пространстве частот).

Это называется дуальностью в представлении сигналов. Эти формы представления сигнала эквивалентны.

Спектральное представление сигнала:

Сигналы бывают детерминированные и случайные. Для случайных сигналов определены только вероятностные характеристики (для них нет спектра), но зная вероятностные характеристики, можно определить энергетический спектр. Для детерминированных сигналов характерны определенные значения частоты, т.е. можно говорить о спектре.

Р ассмотрим пример:

Т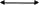

- скважность, где Т-период импульса, а τ – длительность импульса.

_, ,

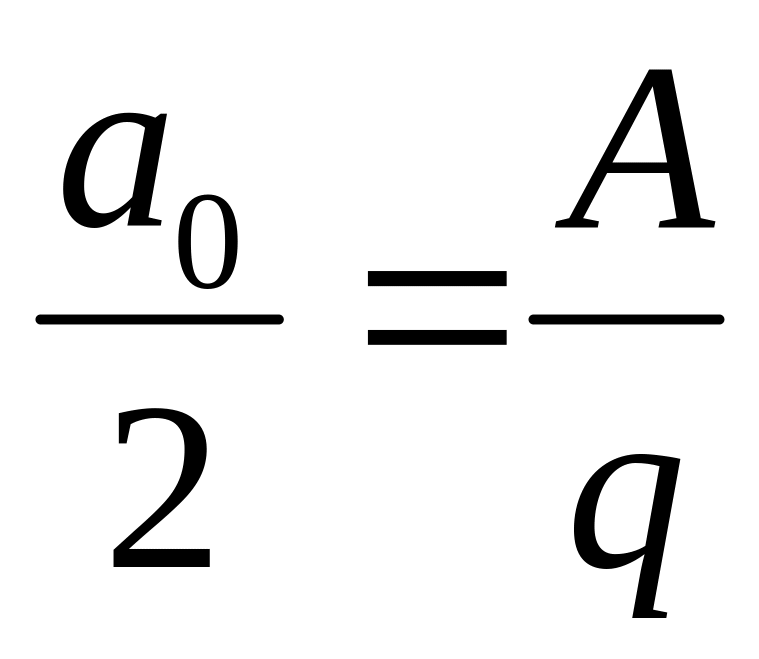где , n - № гармоники, ω₁ – главная гармоника.

Спектр линейчатый, так как функция периодическая.

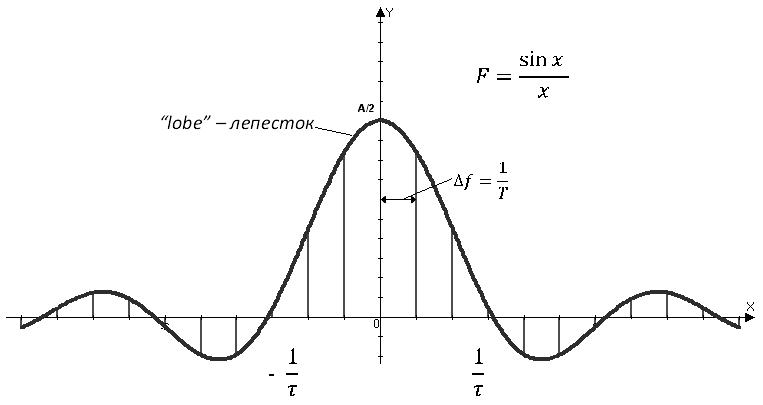
Чем больше период, тем гуще спектр. Поэтому обычно T увеличивают, чтобы повысить точность разрешения по частоте. Чем короче импульс, тем более широкий диапазон частот занимает, т. е. для коротких импульсов спектр расширяется по частоте, а для длинных – сужается.

Чаще рисуют модуль:

П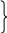 ринцип непределённости: Ограниченная по частоте функция бесконечна по длительности (и наоборот)

∆f – ширина спектра ∆f* τ = const

τ – длительность импульса

Дельта функция Дирака

δ-функция определяется так:

δ(х)=0, если х≠0 δ(х)→∞, если х=0

Отсюда следует единственное полезное свойство δ-функции – стробирующее (фильтрующее) свойство:

Если знать мгновенное значение сигнала в какой-то момент времени, то можно вырезать «кусок» функции, где дельта функция определена.

Интеграл несобственный, является функционалом, то есть ставится в соответствие число к функции.

δ-функция – это производная единичного скачка (ф-ция Хевисайда):

Докажем ещё один вариант определения δ-функции:

Замена:

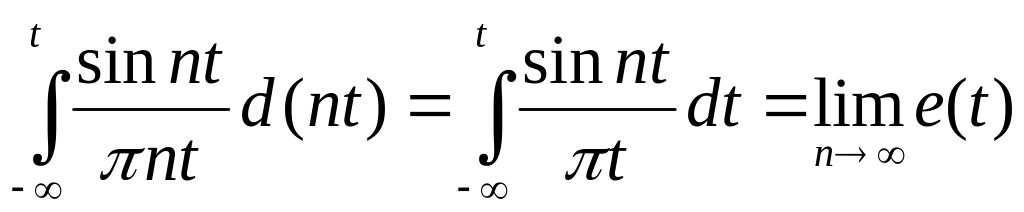
Ещё одно соотношение:

Преобразование Фурье

Периодических сигналов в природе очень мало. В общем случае они непериодические. Но для их представления в пространстве частот нужны преобразования Фурье.

Спектр непериодического сигнала

Сделаем из непериодической функции периодическую, для этого аналитически продолжим функцию. Это метод аналитического продолжения: размножение функции в обе стороны на бесконечном интервале.

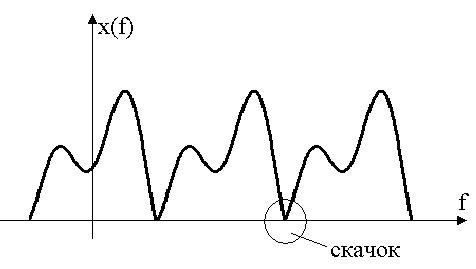
Теперь у нас периодическая функция → раскладываем в ряд Фурье → преобразование Фурье (за спектр при бесконечном разложении принимается спектр одной части (в пределе)).

Скачок – нарушение условий Дирихле. Спектр получить можно, но обратным преобразованием сигнал получить не сможем, возникнут искажения. Скачок (из-за разрыва на концах отрезка) дает паразитные явления → явления Гиббса.

Метод борьбы – использование «оконных функций». Чтобы убрать искажения надо умножить функцию на «окно». «Окно» сглаживает место стыковки.

, где – функция окна.

Используют различную форму окон – прямоугольное, треугольное и т.д. Требования, предъявляемые к функции окна – должны быть производные равны нулю.

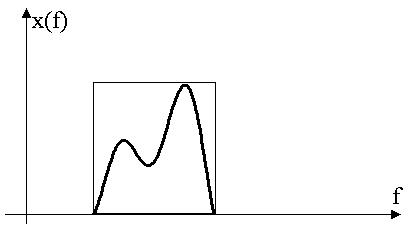
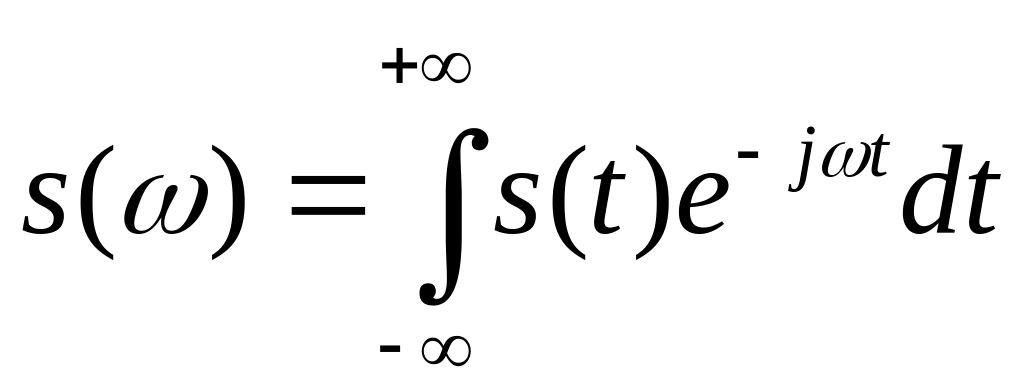- прямое преобразование Фурье

- обратное преобразование Фурье

Если спектр симметричен, то сигнал действительный. Если спектр несимметричен, то сигнал мнимый.

Пример: Найти спектр одиночного импульса.

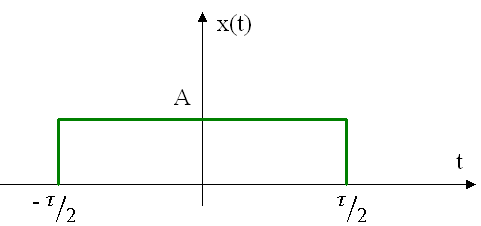
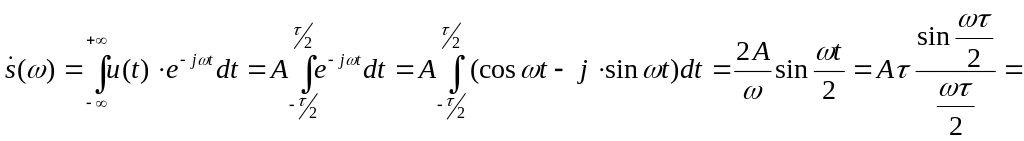
Cвойства Фурье:

- спектр комплексный

- ∆f* τ = const

- можно восстановить ф-цию времени по комплексному сигналу, но чтобы восстановленная ф-ция была действительной, её спектр должен быть симметричным.

Свертка двух функций во временной области: скалярное произведение функций, одна из которых сдвинута по времени.

Свертка двух функций в частотной области:

Если умножать две функции во временной области, то в частотной области их спектры свёртываются, и наоборот.

Корреляция двух функций: кросскорреляционная и автокорреляционная функции

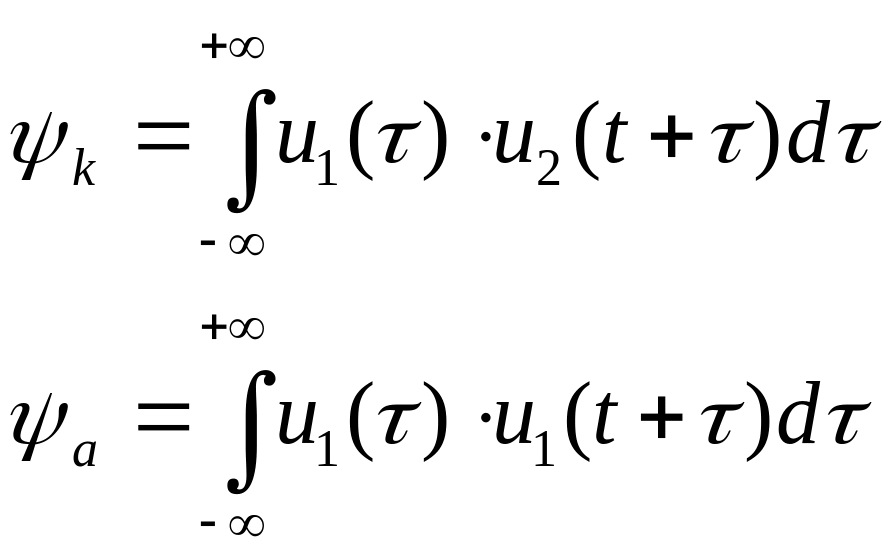
Функция корреляции ищет сигнал, похожий на первоначальный. Она определяет максимальное статическое совпадение двух функций.

Свойство сдвига одной функции, относительно другой: Когда они наложены, то корреляция максимальна. Если находятся на расстоянии, то минимальна.