
- •1) Электронная конфигурация внешних оболочек атомов и типы сил связи в твердых телах.
- •2) Структуры важнейших полупроводников - элементов aiv, avi и соединений типов аiiiвv,
- •3) Симметрия кристаллов.
- •4)Трансляционная симметрия кристаллов.
- •5) Базис и кристаллическая структура.
- •6) Элементарная ячейка.
- •7) Примитивная ячейка.
- •8) Ячейка Вигнера—Зейтца. Решетка Браве.
- •Решетки Бравэ
- •9) Обозначения узлов, направлений и плоскостей в кристалле.
- •10) Обратная решетка, ее свойства.
- •11) Зона Бриллюэна.
- •Характерные точки зоны Бриллюэна
- •Интересные особенности
- •12) Примеси и структурные дефекты в кристаллических и аморфных полупроводниках.
- •13) Химическая природа и электронные свойства примесей.
- •14) Точечные, линейные и двумерные дефекты.
- •Источники и стоки точечных дефектов
- •Комплексы точечных дефектов
- •Одномерные дефекты
- •Двумерные дефекты
- •Трёхмерные дефекты
- •21) Основные приближения зонной теории.
- •22) Волновая функция электрона в периодическом поле кристалла.
- •23) Зона Бриллюэна.
- •24) Энергетические зоны.
- •25) Эффективная масса.
- •Эффективная масса для некоторых полупроводников
- •26) Плотность состояний.
- •Определение
- •27) Уравнения движения электронов и дырок во внешних полях.
- •28) Искривление энергетических зон в электрическом поле.
- •29) Связь зонной структуры с оптическими свойствами полупроводника.
- •30) Уровни энергии, создаваемые примесными центрами в полупроводниках.
- •31) Доноры и акцепторы.
- •32) Мелкие и глубокие уровни.
- •33) Водородоподобные примесные центры.
- •42) Проводимость, постоянная Холла и термо-эдс. По характеру проводимости. Собственная проводимость
- •Примесная проводимость
- •43) Дрейфовая скорость, дрейфовая и холловская подвижности, фактор Холла.
- •44) Дрейфовый и диффузионный ток.
- •45) Соотношение Эйнштейна.
- •46) Механизмы рассеяния носителей заряда в неидеальной решетке.
- •47) Взаимодействие носителей заряда с акустическими и оптическими фононами.
- •48) Рассеяние носителей заряда на заряженных и нейтральных примесях.
- •49) Генерация и рекомбинация неравновесных носителей заряда.
- •50)Уравнение кинетики рекомбинации.
- •51) Времена жизни.
- •52) Фотопроводимость.
- •53) Механизмы рекомбинации.
- •54) Излучательная и безызлучательная рекомбинация.
- •55) Межзонная рекомбинация.
- •56) Рекомбинация через уровни примесей и дефектов.
- •57) Центры прилипания.
- •59) Схема энергетических зон в контакте металл-полупроводник.
- •60) Обогащенные, обедненные и инверсионные слои пространственного заряда вблизи контакта.
- •61) Вольт-амперная характеристика барьера Шоттки.
- •62) Энергетическая диаграмма р-п перехода.
- •63) Инжекция неосновных носителей заряда в р-п переходе.
- •64) Гетеропереходы.
- •65) Энергетические диаграммы гетеропереходов.
23) Зона Бриллюэна.
Вектор р (или к = р/ћ) характеризует закон преобразования волновой функции электрона при сдвиге ее аргумента на какой-либо вектор решетки. Разным собственным функциям соответствуют, вообще говоря, различные значения квазиимпульса (квазиволнового вектора). Поэтому компоненты его (как и компоненты импульса в случае свободного электрона) следует рассматривать как квантовые числа, характеризующие данное стационарное состояние. Однако, в отличие от компонент импульса и от квантовых чисел, встречающихся в теории атома, квазиимпульс определяется в принципе неоднозначно. Действительно, обозначим через с вектор, скалярное произведение которого на аn есть целое кратное 2лй:
аnс = 2лН x (целое число). (3.2)
Следовательно, векторы р и р + с физически эквивалентны: оба они определяют одно и то же преобразование волновой функции.
Нетрудно найти явный вид вектора с. Для этого следует лишь ввести понятие обратной решетки. Основные векторы последней b1, b2, b3 определяются равенствами
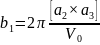 ,
,
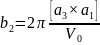 ,
,
 (3.3)
(3.3)
где
V0
=
| (а1
[а2 а3])
| есть объем параллелепипеда, построенного
на векторах a1,
a2,
а3
(объем элементарной ячейки). В частности,
в простой кубической решетке, когда а1
=
а2
=
а3
= а и
b1
= b2
=
b3
= b,
мы
имеем
а3])
| есть объем параллелепипеда, построенного
на векторах a1,
a2,
а3
(объем элементарной ячейки). В частности,
в простой кубической решетке, когда а1
=
а2
=
а3
= а и
b1
= b2
=
b3
= b,
мы
имеем
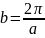 (3.3')
(3.3')
Очевидно, векторы b1, b2, b3 имеют размерность обратной длины. На основных векторах b1, b2, b3 можно построить периодическую решетку. Она и называется обратной (по отношению к прямой решетке данного кристалла).
Произвольный вектор обратной решетки имеет вид
bm = m1b1 + m2b2 + m3b3, (3.4)
где т1, т2, т3 — положительные или отрицательные целые числа или нули (при этом т1, т2 и т3 не равны нулю одновременно), т = { т1, т2, т3 }.
Элементарная ячейка обратной решетки представляет собой параллелепипед, построенный на векторах b1, b2, b3. «Объем» этого параллелепипеда равен | (b1 [b2 x b3]) | (разумеется, он имеет размерность обратного объема). Подставляя сюда формулы (3.3) для b1, b2, b3 и раскрывая получающееся произведение, находим
|(b1 [b2 х b3]) | = (2π)3/V0. (3.5)
Как и в случае прямой решетки, выбор элементарной ячейки в обратной решетке неоднозначен и определяется соображениями удобства.
Другой способ построения элементарной ячейки состоит в следующем. Какой-то узел обратной решетки выбирают в качестве начала координат и соединяют его прямыми линиями с ближайшими к нему узлами. Через середины этих линий перпендикулярно к ним проводят плоскости. В качестве элементарной ячейки обратной решетки можно выбрать наименьший многогранник, ограниченный так построенными плоскостями и содержащий внутри себя начало координат. Этот многогранник называется ячейкой Вигнера — Зейтца.
Такие многогранники можно построить около любого узла решетки; при этом они не перекрываются и совокупность их заполняет все обратное пространство. Отсюда следует, что объем одного многогранника действительно равен (2π)3/V0, как это и должно быть. В отличие от параллелепипеда, построенного на векторах b1, b2, b3, элементарная ячейка, выбранная указанным только что образом, обладает всеми свойствами симметрии обратной решетки.
Из определения (3.3) вытекают равенства
а1b1 = а2b2 = а3b3 = 2π,
аαbβ = 0, α ≠ β (α, β = 1,2,3).
Умножим теперь произвольный вектор решетки на вектор обратной решетки (3.4). Пользуясь соотношениями (3.6), мы получаем
anbm = (п1т1 + п2т2 + п3т3) 2π.
В скобках в правой части этого равенства стоит целое число, и, следовательно, вектор с, удовлетворяющий условию (3.2), можно записать в виде
с = ћ bm. (3.7)
Итак, квазиимпульс определен лишь с точностью до вектора обратной решетки, умноженного на ћ. Это обстоятельство позволяет ограничить изменение компонент квазиимпульса конечной областью, исчерпывающей все физически неэквивалентные их значения. Такая область — совокупность всех физически неэквивалентных значений квазиимпульса — называется зоной Бриллюэна. В силу произвольности вектора bт в (3.7) выбор ее неоднозначен. Так, можно выбрать в качестве зоны Бриллюэна область, определяемую неравенствами
— π ћ < ра1 ≤ π ћ,
— π ћ < ра2 ≤ π ћ, (3.8)
— π ћ <ра3 ≤ π ћ.
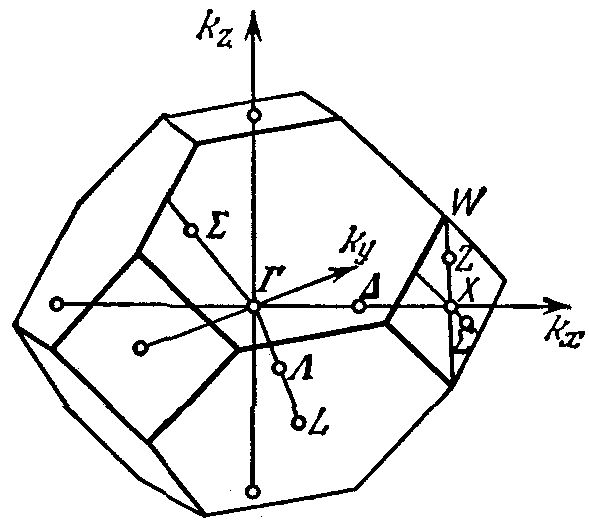
Рис. 3.1. Первая зона Бриллюэна для решеток типа алмаза и цинковой обманки. |
Эти неравенства определяют некоторый параллелепипед в p-пространстве, содержащий в себе начало координат. Его называют первой зоной Бриллюэна. Можно определить первую зону Бриллюэна и для компонент квазиволнового вектора k: надо лишь заменить р на k в неравенствах (3.8), опустив множители ћ. Квазиимпульс (или квазиволновой вектор), изменяющийся в пределах первой зоны Бриллюэна, называется приведенным. В частности, в простой кубической решетке векторы а1, а2, а3 одинаковы по величине (равной постоянной решетки а) и направлены по трем взаимно перпендикулярным осям куба. Выбирая эти оси в качестве координатных, получаем из (3.8) для данного частного случая
|
Первая
зона Бриллюэна здесь представляет
собой куб объема
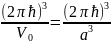 .
В k-пространстве
соответствующий объем равен (2π)3/V0.
.
В k-пространстве
соответствующий объем равен (2π)3/V0.
Выбирая другие периоды рx, рy, pz, мы получим вторую, третью и т. д. зоны Бриллюэна.
Таким образом, зона Бриллюэна есть чисто геометрическое понятие: форма ее зависит только от структуры решетки, но не от природы действующих в ней сил. Более того, как видно из предыдущего, зона Бриллюэна определяется только основными векторами решетки. Следовательно, она одна и та же как для простых, так и для базисных решеток одной и той же сингонии, например для простой гранецентрированной решетки и для решетки типа алмаза.

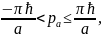 а
= х, у, z.
(3.8’)
а
= х, у, z.
(3.8’)