Свойства интегралов:

Т к вычисление интегр-лов сводится к вычислению 2х криволин-х интег-лов 2го рода , то интегралл ф-ии комплексного переменного обладает всеми теми же св-ми

1) где Г’-кривая проходимая в обратном направлении

2) из св-ва 2) вытекает, то теорему о сущ-нии интегр-ла можно распромт-ть на кусочно гладкие кривые

3)Линейность 4) 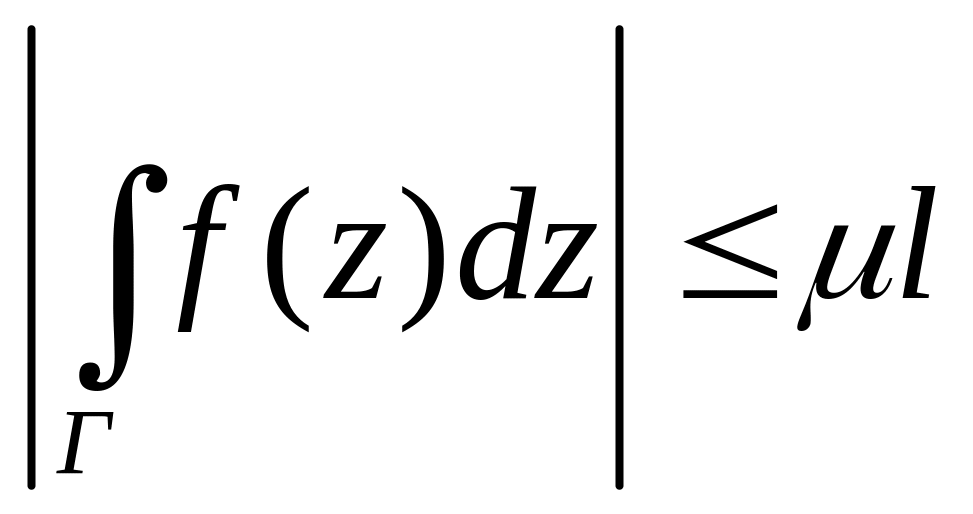где l- длинна Г

13. Интегральная теорема Коши.

Данная теорема является одной из центральных теорем аналитических функций комплексной переменной.

Теорема: Пусть функция аналитична в односвязной области D конечной плоскости и Г-замкнутая спрямляемая кривая целиком лежащая в области D,тогда:

Опр: область D – односвязная, если любая кусочногладкая, простая, замкнутая кривая целиком леащая в области D ограничевает область, все точки которой принадлежат области D.

Замечание: область D является односвязной, если ее граница состоит из 1ой простой замкнутой кривой.

Опр: Область D – n-связная,если ее граница состоит из n замкнутых кривых не имеющих общих точек.

ПР: 5ти связная.

Теорема Коши. Док-во:

Докажем теорему Коши при дополнительном условии что f’(z) – непрерывна в области D.

Пусть - аналитич-я,то U(x,y) и V(x,y) - диффиренцируемые.

По теореме

-непрерывны,тогда для каждого криволинейного интеграла справедлива формула грина:

получаем:

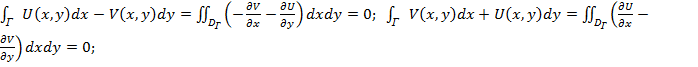
В силу того, что f(z)-аналитична, то выполняется условие Коши-римана:

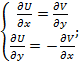значит

Пр:

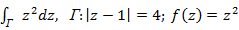1. , аналитична по всей плоскости, Г – окружность с центром в точке 1, R=4,т.е это замкнутая криваыя, значит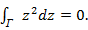

Замечание: теорема коши справедлива и в случае многосвязной области при условии,что кривая Г ограничивает область,целиком сост. Из точек принадлижащих D.

Следствие: Если Г1 и Г2 – 2 спрямляемые кривые, целиком лежащие в области D аналитичности функции f(z), имеющие общие конец и начало,то , т.е интеграл не зависит от пути интегрирования.

Док-во: , т.к ограничена нужная область => .

Теорема. Пусть f(z) аналитична в двусвязной области D, границей кот.являются кривые Г и . Тогда

Док-во. Проведем в области D разрез,соединяющий граничные кривые. Рассм.область,границей которой являются кривые Г, и L. Эта область является односвязной.

Значит,

Пример. где Г-произвольная замкнутая кривая,охватывающая точку а.

Рассмотрим окрестность - так,чтобы она целиком лежала в области,огранич. Г. Тогда аналитична в двусвязной области. Значит,

14. Первооброзная. Формула Ньютона-Лейбница.

теор. если f(z) аналитична в обл. D то F(z) так же аналитична в D, причем справедливо равенство F’(z)=f(z) zD.

опр.: ф-ция Ф(z) наз. первообразной для f(z) если она аналитична в обл. D и справедливо р-во: Ф’(z)=f(z) zD.

Вспомогат. фундам. теор.: .

док-во:

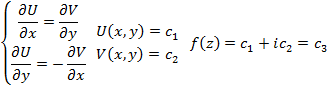
теор.: Если F(z) и Ф(z) явл. первообразными для f(z)в обл. D, то Ф(z)=F(z)+c, c=const.

ф-ла Ньютона-Лейбница: Г - произв. кривая с началом в т. z₁ и концов в т z₂ и f(z) аналитична в некот. обл. D содержащей Г. Тогда: .

15. Интегральная формула Коши.

Теор. Пусть ф-ция f(z) аналитична в односвязн. обл. D и на ее границе Г, тогда aD справеливо .

док-во: рассм. произв. aD. Выберем произв. ε>0, т.к. f(z) аналит. в т. a, то и непрерывна в ней, тогда ε>0 δ>0 zD |z-a|<δ => |f(z)-f(a)|<ε. Рассм. круг с ц. в т. a радиуса r<δ, K(a,r) и обозн. его границу Г. Рассм. ф-цию f(z)/z-a - аналит. в обл. D, за искл. т. a, а значит аналит. в двусвязн. обл., получ. из D исключением круга K(a,r). Тогда по следств. из теор. Коши: . Покажем, что он равен f(a):

; Покажем, что первое слагаемое = 0

зам. если ф-ция аналит. в D и на ее границе, то она однозн. опред. через свои знач. на границе Г: .

зам. если т. a лежит во внешности контура Г, то .