
- •1.Плоскость комплексных чисел. Модуль, аргумент комплексного числа. Тригонометрическая форма записи комплексного числа.
- •2. Предел последовательности комплексных чисел.
- •3. Числовые ряды с комплексными членами.
- •4. Понятие функции комплексной переменной. Примеры.
- •Линейная ф-ция. Ее геометрический смысл.
- •7. Понятие производной функции комплексной переменной. Условия Коши-Римана.
- •8. Геометрический смысл модуля и аргумента производной. Понятие конформного отображения.
- •9. Показательная ф-ция и ее св-ва.
- •10. Логарифмическая функция и ее свойства.
- •Свойства логарифмической функции:
- •Свойства главного логарифма:
- •11. Тригонометрические ф-ции.
- •12. Понятие интеграла от функции комплексной переменной. Условия существования интеграла от функции комплексной переменной.
- •Свойства интегралов:
- •13. Интегральная теорема Коши.
- •14. Первооброзная. Формула Ньютона-Лейбница.
- •15. Интегральная формула Коши.
- •16.Понятие функционального ряда. Равномерная сходимость функциональных рядов.
- •17. Степенные ряды.
- •18. Аналитическая ф-ция. Разложение в ряд.
- •19. Теорема единственности.
- •20. Аналитическое продолжение.
- •21. Теорема Лиувилля.
- •22. Нули аналитической функции.
- •23. Ряд Лорана. Теор. Лорана.
- •24. Устранимые особые точки.
- •25. Полюсы функции комплексной переменной.
- •Необходимость.
- •Достаточность.
- •26. Существенно особые точки функции комплексной переменной. Теорема Сохоцкого-Вейерштрасса.
- •Достаточность.
- •27. Вычет функции. Теорема о вычетах.
- •28. Понятие логарифмического вычета. Принцип аргумента.
- •29. Теорема Руше.
- •30. Основная теорема алгебры.
9. Показательная ф-ция и ее св-ва.
Опред. ф-цию w=ez след. образом: ez=ex+iy=ex(cosy+isiny). (если Jm(z)=0, z=x, то ez=ex).
Осн.
св-ва:
1.
| ez|=
ex;
2.
если Re(z)=0,
z=iy,
то ez=cosy+isiny
(ф-ла Эйлера); 3.
ez
явл. аналитичной во всей комп. пл-ти,
причем (ez)’=
ez;
4.
![]() ,док-во:
,док-во:
![]() ;
5.
ф-ция ez
явл. периодической с периодом T0=2πi;
6.
ф-ция w=ez
осущ. конформное отображение комп.
пл-ти;
;
5.
ф-ция ez
явл. периодической с периодом T0=2πi;
6.
ф-ция w=ez
осущ. конформное отображение комп.
пл-ти;
10. Логарифмическая функция и ее свойства.
Число
w
называется натуральным логарифмом
комплекс. Числа z,
если ew=z;
обозначается
![]() lnz.
lnz.
Теорема. Любое отличное от нуля комплексное число z имеет бесконечно много логарифмов, которые определяются по формуле:
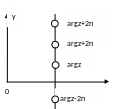
Lnz=ln|z|+i(argz+2k), (kZ)
Док-во. Пусть w=u+iv , z=x+iy
w=lnz
ew=z
eu+iv=x+iyeu*cosv+ieu*sinv=x+iy![]() А можно записать x+iy
в тригонометрической форме:
А можно записать x+iy
в тригонометрической форме:
eu(cosv+isinv)=|z|(cos+isin) => Lnz=lnz+i(argz+2k).
Пример. Ln(-1)
Ln(-1)=ln|-1|+i(arg(-1)+2k)=i(+2k), kZ
Замечание. Все логарифмы комплекского числа z расположены на прямой, параллельной линии оси. Если z=xR+ , то все логарифмы будут мнимыми.
Свойства логарифмической функции:
Функция w=lnz является многозначной;
Для любых z1,z2C\{0} ln(z1,z2)=lnz1+lnz2; ln(z1/z2)=lnz1-lnz2
Замечание. Последние равенства понимаются как равенство двух множеств.
Пример. Ln((-1)+1)=ln(-1)=i =>Ln(-1)+ln1=i*3+0=3i
Значения различны, но множества совпадают.
Замечание. Главным логарифмом z для действительных чисел совпадает со школьным логарифмом.
Свойства главного логарифма:
Главный логарифм определен для любого zC\{0}
Главный логарифм – непрерывная функция на всей комплексной плоскости с разрезом вдоль отрицательной действительной полуоси.
Главный логарифм – аналитическая функция во всей комплексной плоскости с разрезом вдоль отрицательной действительной полуоси: (lnz)’=1/z
11. Тригонометрические ф-ции.
синус
комп. числа z
опред. по формуле: ![]() ;
;
косинус
комп. числа z
оред. по формуле: ![]() ;
;
зам.
данные определения естественны (![]() ).
).
Осн.
св-ва:
1.
cos
- четная ф-ция, sin
- нечетная ф-ция. 2.
sin
и cos
явл. периодическими с периодом 2π. 3.
Для sin
и cos
сохр. все привычные тригоном. тождества
(как ![]() ).
4.
sin
и cos
явл. аналит. во всей комп. пл-ти. 5.
sin
и cos
явл. неограниченными.
).
4.
sin
и cos
явл. аналит. во всей комп. пл-ти. 5.
sin
и cos
явл. неограниченными.
опр.
гиперб. косинусом наз. величина ![]() .
.
6.
![]()
12. Понятие интеграла от функции комплексной переменной. Условия существования интеграла от функции комплексной переменной.
Пусть на плоскости компл. переме-го задана спрямляемая кривая Г и вдоль этой кривой определена функция w=f(z)
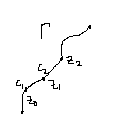 Разобьем
кривую Г точками z0,
z1…
на частичные дуги и выберем на каждой
из этих дуг произвольную точку
Разобьем
кривую Г точками z0,
z1…
на частичные дуги и выберем на каждой
из этих дуг произвольную точку
![]() где (k=1…n)
где (k=1…n)
Составим
сумму
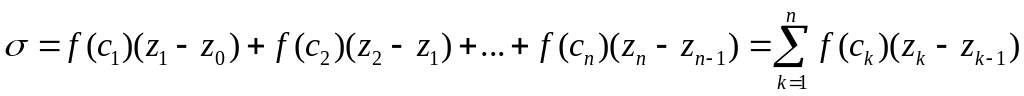 Опр:
сумму вида
Опр:
сумму вида
![]() наз-ся интегральной суммой для ф-ии
наз-ся интегральной суммой для ф-ии
![]() на кривой
соответствующей данному разбиению
кривой на частичные дуги и выбора точек
С.
на кривой
соответствующей данному разбиению
кривой на частичные дуги и выбора точек
С.
Обозначим
через
![]() наибольшую из длин
наибольшую из длин
![]()
Опр:Если
сущ-ет конечный придел интегральных
сумм
при
![]() ,
то его называют интегралом от ф-ии
,
то его называют интегралом от ф-ии
![]() по кривой Г и обозначают
по кривой Г и обозначают
![]()
Замечание:
если кривая Г лежит в
![]() ,
а
ф-я переменной x,
то понятие интеграла ф-ии
совпадает
с обычным опред. интегралом. (Опред.
интеграл это частный случай интеграла
от ф-ии комплексной переменной)
,
а
ф-я переменной x,
то понятие интеграла ф-ии
совпадает
с обычным опред. интегралом. (Опред.
интеграл это частный случай интеграла
от ф-ии комплексной переменной)
Теорема(Если Г-гладкая кривая на плоскости, а ф-я неприрывная на Г, то сущ.интегралл )
Док-во:
Покажем,
что сущ. придел интегрир-я суммы
![]()
![]()
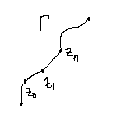 Разобьем
кривую Г точками z0,
z1…
Разобьем
кривую Г точками z0,
z1…
![]() выберем на каждой из частичных дуг
точку
где (k=1…n)
и пусть задана:
выберем на каждой из частичных дуг
точку
где (k=1…n)
и пусть задана:
![]() введем
обозначение
введем
обозначение
![]()
![]()
![]()
Составим интегральную сумму:
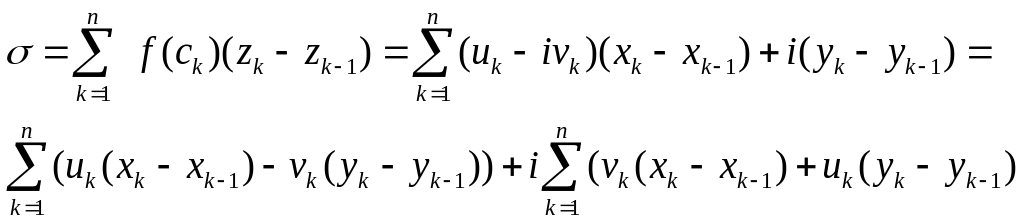
Обозначим
![]()
![]()
Заметим,
что
![]() является
интегрир. суммой для ф-ии u(x,y)-v(x,y)
вдоль кривой Г, а
является
интегрир. суммой для ф-ии u(x,y)-v(x,y)
вдоль кривой Г, а
![]() -
интегрир. сумма для v(x,y)+u(x,y)
-
интегрир. сумма для v(x,y)+u(x,y)
Т к неприрывна вдоль кривой Г, значит неприрывны u(x,y) и v(x,y) (а значит по т со 2 курса) существуют приделы
![]()
![]() где
d-это
диаметр разбиения кривой Г на частичные
дуги из опр-я криволин-го интеграла 2-го
рода Т к
где
d-это
диаметр разбиения кривой Г на частичные
дуги из опр-я криволин-го интеграла 2-го
рода Т к
![]() ,
то
,
то
![]() значит:
значит:
 Замечание:
1) из док-ва видно, что вычисление интег-ла
сводиться к вычислению 2х интег-лов 2го
рода
Замечание:
1) из док-ва видно, что вычисление интег-ла
сводиться к вычислению 2х интег-лов 2го
рода
2)
Если Г=[a,b]
и ф-я
![]() то
то
![]() пользуясь
формулой для вычисления криволин-го
интеграла :
пользуясь
формулой для вычисления криволин-го
интеграла :
![]()

![]()
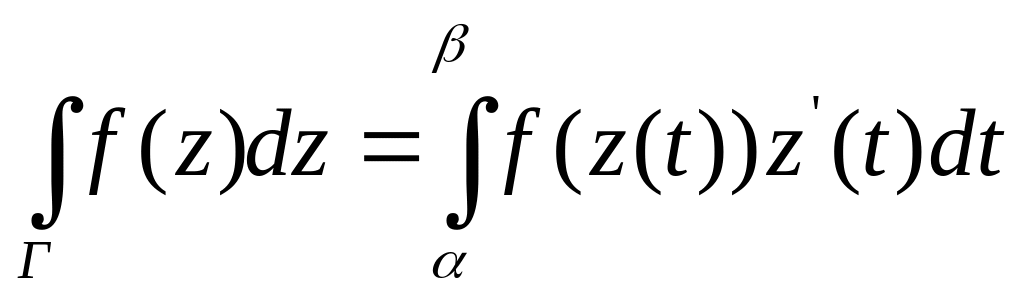
Пример:
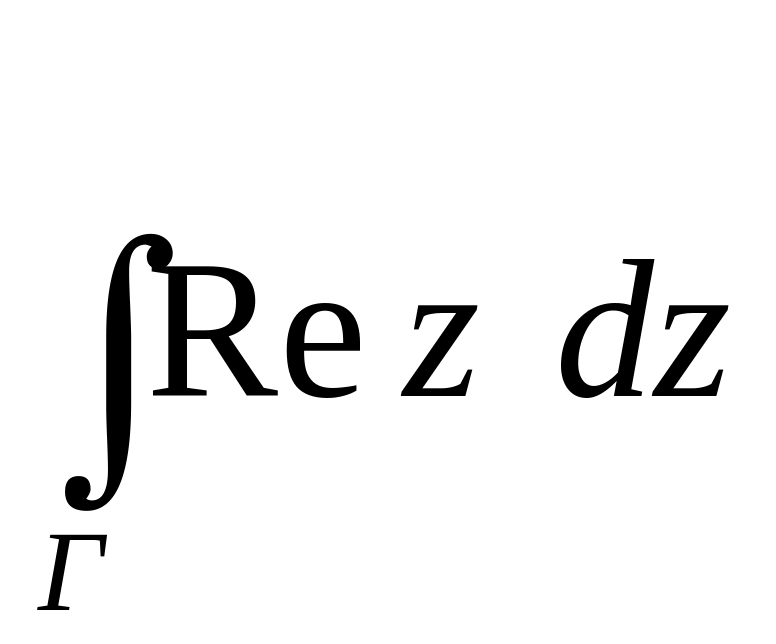 где
Г=[-1+i;1-2i]
где
Г=[-1+i;1-2i]
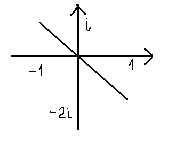
Зададим прямую проходящую (-1;1) (1;-2)
![]()
![]()
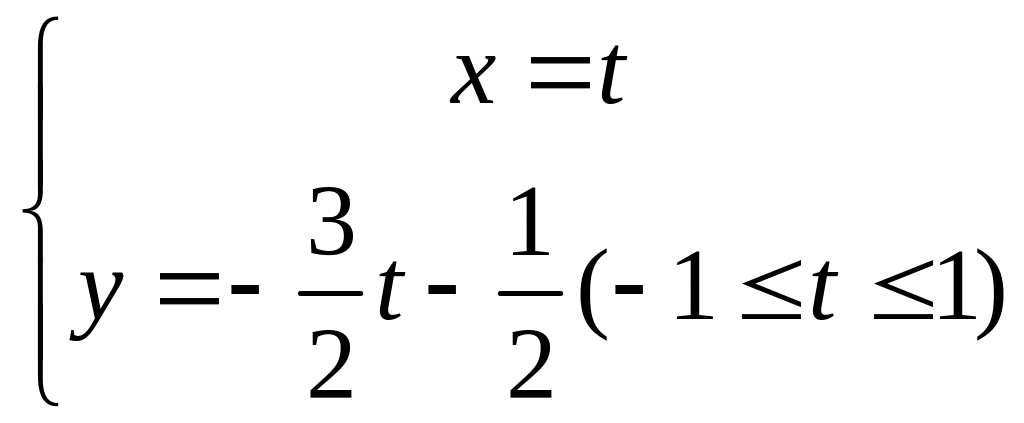
![]()
![]()
