Основные математические методы. Уравнения Максвелла.

1) TdS = dU + dL. Применяя чисто математические методы, мы можем на основе этого уравнения получить соотношения, устанавливающие связи между различными термодинамическими свойствами вещества. Как уже отмечалось, все термодинамические величины можно подразделить на две группы — функции состояния и функции процесса. Функции состояния

однозначно определяются параметрами данного состояния. Следовательно, для определения изменения функции состояния необходимо знать лишь значения этой функции в начале и в конце процесса. Функции процесса (например, работа и теплота) определяются характером

процесса изменения состояния термодинамической системы. Как было показано в гл. 2, характерное свойство функций состояния заключается в том, что их дифференциал является полным дифференциалом.Напомним, что в математическом анализе полным дифференциалом функции нескольких независимых переменных z = f(x, у, w…) называют величину вида В подавляющем большинстве случаев для чистых веществ мы будем рассматривать функции двух переменных z = f (x, у), для которых Частные производные взяты при условии постоянства тех величин, которые

стоят в виде индекса. Например, производная от давления по температуре ∂р/∂Т

может быть вычислена для различных условий: при условии постоянства объема

системы v, при постоянной энтальпии системы h, постоянной энтропии системы

s и т.д. В каждом из этих случаев рассматриваемая производная, обозначаемая

соответственно (∂р/∂Т)v, (∂р/∂Т)h, (∂р/∂Т)s и т.д., будет иметь, вообще говоря,

различное значение. Из математического анализа известно, что т.е. значение смешанной производной не зависит от последовательности диффе-

ренцирования. Отсюда следует, что если дифференциал какой-либо функции z = f (x, у)

записан в виде dz = Mdx + Ndy

и если известно, что дифференциал функции z является полным дифференциа-

лом, то справедливо следующее соотношение: В дальнейшем это уравнение поможет нам получить важные дифференциальные уравнения термодинамики. 2)Запишем уравнение в следующем виде: du = Tds – рdv. Обозначим через х и у две условные переменные, под которыми будем подразумевать любую пару из четырех величин: р, v, Т и s. Из уравнения этого получаем:

Дифференцируя первое из этих уравнений по у, а второе по х, получаем соответственно:

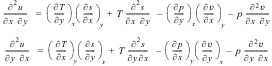
Приравнивая правые части этих уравнений, получаем:

Поскольку (∂s/∂p)s = 0, (∂p/∂s)p = 0 и поскольку, разумеется, (∂s/∂s)p = 1 и (∂p/∂p)s = 1, получаем:

Если вместо х и у подставим v и s, р и Т, v и Т, то получим соответственно:

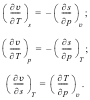
Эти четыре дифференциальных уравнения (уравнения Максвелла) будут неоднократно использованы в термодинамике

Частные производные внутренней энергии и энтальпии

Рассмотрим некоторые наиболее важные соотношения для частных производных внутренней энергии и энтальпии. Подставляя значение (∂s/∂v)T из уравнения Максвелла находим Это соотношение характеризует зависимость внутренней энергии от объема в изотермическом процессе. Аналогичным путем получаем соотношение, характеризующее зависимость внутренней энергии от давления в изотермическом процессе: Это соотношение характеризует зависимость энтальпии от давления в изотермическом процессе. Аналогичным образом может быть получено соотношение, характеризующее зависимость энтальпии от объема в изотермическом процессе: Полученные в этом параграфе уравнения, имеют большое значение для термодинамических исследований свойств веществ.Уравнения позволяют, используя данные о термических свойствах вещества (удельный объем в зависимости от температуры и давления),

находить калорические величины — внутреннюю энергию и энтальпию, а также решать и обратную задачу — по известным калорическим величинам вычислять термические свойства вещества. Энтальпию вещества при данных давлении р

и температуре Т находим, интегрируя уравнение здесь h(p0, T) — энтальпия вещества в некотором начальном состоянии, имеющем ту же температуру Т, но другое значение давления p0. Аналогичным образом 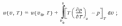здесь u(v0, T) — внутренняя энергия вещества в состоянии, имеющем ту же тем-

пературу Т, но иной удельный объем v0. Располагая данными о термических свойствах вещества, можно вычислитьинтегралы, стоящие в правых частях уравнений .очевидно, что при этом предварительно нужно будет вычислить производные или . Заметим, что в обоих случаях интегрирование ведется вдоль изотермы. Следует подчеркнуть, что уравнения позволяют вычислить не абсолютные значения h и u в данном состоянии — эта задача неразрешима методами одной только термодинамики, — а лишь разность между значением h

или u в данном состоянии и значени

Условия устойчивости и равновесия в изолированной однородной системе Специальный термодинамический анализ позволяет показать, что из соображений термодинамической устойчивости системы для любого вещества должны

выполняться следующие соотношения:с_v > 0 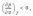т.е., во-первых, изохорная теплоемкость с_v всегда положительна и, во-вторых, в изотермическом процессе увеличение давления всегда приводит к уменьшению объема вещества. Условие 1 называют условием термической

устойчивости, а условие 2 — условием механической устой чивости. Условия 1 и 2 можно объяснить так называемым принципом смещения равновесия (принцип Ле Шателье—Брауна), смысл которого заключается в том, что, если система, находившаяся в равновесии, выводится из него, соответствующие параметры системы изменяются таким образом, чтобы система вернулась в состояние равновесия Эти условия термодинамической устойчивости системы ясны и без формаль ных выкладок. Представим себе, что теплоемкость сv некоторого вещества отрицательна. Это означало бы, поскольку c_v = dq_v/dT, что подвод теплоты к веществу при постоянном объеме этого вещества приводил бы не к повышению, а к понижению температуры. Таким образом, чем больше теплоты мы подводили бы к веществу в изохорном процессе, тем больше становилась бы разность между температурами этого вещества и источника теплоты

(окружающая среда). В результате увеличения перепада температуры между веществом и источником теплоты система, состоящая из рассматриваемого вещества и источника теплоты при неизменном объеме системы, все дальше и дальше отклонялась бы от состояния равновесия вместо того, чтобы стремиться к нему, причем этот процесс развивался бы все быстрее1). Таким образом, система была бы неустойчивой — любая возникшая по тем или иным причинам

даже ничтожно малая разность температур между исследуемым веществом и окружающей средой приводила бы к лавинообразному нарастанию неустойчивости системы. Напротив, аналогичные рассуждения для случая, когда с_v > 0, приводят нас к логичному выводу о том, что процесс теплообмена между рассматриваемым веществом и окружающей средой, сопровождающийся ростом температуры вещества, прекратится тогда, когда температуры среды и вещества сравняются и в системе установится равновесие.

Фазовый переход жидкость — пар, твердое тело — жидкость, твердое тело — пар.

Применительно к фазовому переходу жидкость — пар уравнение можно записать следующим образом где r — теплота парообразования; v′′ — удельный объем пара на линии насыщения; v′ — удельный объем жидкости на линии насыщения; ps — равновесное

давление в точках фазового перехода жидкость — пар. Если давление пара мало, то удельный объем пара на несколько порядков больше удельного объема жидкости, т.е. v′′ >> v′, и поэтому стоящую в знаменателе правой части уравнения разность v′′ – v′ с достаточной степенью

точности можно заменить просто величиной v′′. Кроме того, если давление пара мало, то этот пар с хорошим приближением можно рассматривать как идеальный газ, а для идеального газа в соответствии с уравнением Клапейрона . Поскольку при низких давлениях теплота парообразования слабо зависит оттемпературы, в ряде случаев величину r можно считать практически не зависящей от температуры. Иными словами, когда мы определяем константу интегрирования не по вели- чине Tн.к, а по известному давлению насыщения при какой-либо иной температуре (обозначим ее Т *), уравнение примет вид:

Фазовый переход твердое тело — жидкость. Применительно к фазовому переходу твердое тело — жидкость (плавление) уравнение можно записать в виде где λ — теплота плавления; v_ж — удельный объем жидкости на линии плавления; vтв — удельный объем твердой фазы на линии плавления. Поскольку обычно плотности вещества в жидкой и твердой фазах являются величинами одного порядка, значения v_ж и v_тв близки между собой. При этом

возможны два случая: плотность твердого тела больше плотности жидкости (v_ж > v_тв) и плотность твердого тела меньше плотности жидкости (v_ж < v_тв). Из уравнения очевидно, что в первом случае dp /dT > 0, т.е. с ростом давления температура плавления увеличивается. Во втором случае, когда v_ж < v_тв, величина dp /dT, оказывается отрицательной, т.е. с ростом давления температура плавления уменьшается. Таким образом, у некоторых веществ (например, у воды) кривая плавления в р, T-диаграмме имеет отрицательный наклон.

Применительно к фазовому переходу твердое тело — пар уравнение можно записать в виде где L — теплота сублимации; v_пар — удельный объем пара на линии сублимации; v_тв — удельный объем твердого тела. Поскольку сублимация обычно происходит при низких давлениях (ниже давления в тройной точке), удельный объем пара на линии сублимации на

несколько порядков больше, чем удельный объем вещества в твердой фазе. Поэтому в соответствии с уравнением величина для фазового перехода твердое тело — пар больше нуля, т.е. кривая сублимации в р, T-диаграмме имеет положительный наклон. Очевидно, что при сублимации v_пар >> v_тв и величиной v_тв в уравнении можно пренебречь. Удельный объем пара на линии сублимации с высокой степенью точности описывается уравнением Клапейрона и уравнение приводится к виду Зная температурную зависимость теплоты сублимации, можно проинтегрировать это уравнение.

Фазовые переходы при искривленных поверхностях раздела В случае, когда поверхность раздела фаз не плоская, а искривленная, между фазами возникает разность давлений, обусловленная поверхностным натяжением. Из общего курса физики известно, что на поверхности раздела фаз действует так называемое поверхностное натяжение — сила, стремящаяся сократить до возможного минимума площадь поверхности жидкости. Напомним, что поверхностным натяжением σ называют силу, действующую на единицу длины

п ериметра поверхности; эти силы, нормальные к периметру и касательные к поверхности, изображены стрелками на схеме, представленной на рис. 5.7 (на этом рисунке изображен некоторый мысленно вырезанный участок поверхности раздела фаз). Поскольку на плоской поверхности раздела фаз во всех точках периметра рассматриваемого участка (рис. 5.7, а) силы поверхностного натяжения лежат в одной плоскости, очевидно, что равнодействующая этих сил равна нулю. В случае криволинейной поверхности раздела фаз, как видно из рис. 5.7, б, силы поверхностного натяжения в различных точках периметра участка лежат в разных плоскостях и их равнодействующая уже не равна нулю. При этом очевидно, что эта равнодействующая тем больше, чем больше кривизна поверхности раздела фаз. Нетрудно видеть, что эта равнодействующая направлена к вогнутой стороне поверхности. 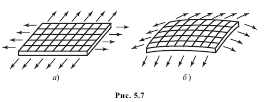Таким образом, на ту фазу, которая расположена под вогнутой стороной поверхности слоя, действует со стороны этого слоя дополнительное давление, обусловленное поверхностным натяжением.У чет сил поверхностного натяжения играет большую роль при анализе различных процессов фазовых превращений, происходящих при искривленной

поверхности раздела фаз. Это уравнение, впервые полученное Лапласом, связывает между собой разность давлений между фазами с силой поверхностного натяжения и кривизной поверхности раздела фаз В этом уравнении фигурируют два радиуса кривизны — ρI и ρII. Это и понятно: как известно из аналитической геометрии, кривизна любой поверхности характеризуется двумя радиусами, определяющими кривизну этой поверхности в двух взаимно перпендикулярных сечениях.

Термодинамические свойства вещества в метастабильном состоянии Оказалось, что если медленно и осторожно (оберегая сосуд от толчков, не допуская попадания

в жидкость извне посторонних частиц, пузырьков газа и т.д.) нагревать чистую, практически не содержащую растворенных газов жидкость в сосуде с гладкими стенками, то удастся нагреть жидкость значительно выше температуры кипения при данном давлении (как говорят, перегреть жидкость). Например, известны опыты, в которых вода при атмосферном давлении перегревалась на десятки градусов. Казалось бы, что при этой температуре вода давно должна была бы превратиться в перегретый пар, но этого не происходило — вода сохраняла все свойства жидкости. Однако если подвергнуть эту систему какому-либо возмущению (например, встряхнуть сосуд), то вода в сосуде мгновенно вскипает и превращается в перегретый пар. Таким образом, очевидно, что состояние перегретой жидкости в соответствии с классификацией, принятой в § 5.2, является метастабильным. Помимо рассмотренного случая перегрева жидкости существуют и другие типы метастабильных состояний вещества — переохлажденный пар (когда тем-пература пара оказывается ниже температуры насыщения при данном давлении) и переохлажденная жидкость (когда температура жидкости оказывается ниже температуры затвердевания при данном давлении). Следует подчеркнуть, что одно и то же метастабильное состояние вещества

может быть получено различными способами. Метастабильное состояние принято характеризовать следующими критериями: для переохлажденного пара — степенью пересыщения пара, под которой понимается отношение плотности пара в данном состоянии к плотности насыщенного пара при той же температуре, а для перегретой жидкости — перегревом, под которым понимается разность между температурой жидкости в данном состоянии и температурой кипения жидкости при том же давлении. Достижимые в тех или иных условиях значения степени пересыщения пара или перегрева жидкости зависят от разнообразных причин, таких как степень шероховатости поверхности сосуда, в котором реализуется метастабильное состояние, степень загрязненности вещества, наличие внешних возмущений и т.д. В наиболее

тщательно поставленных экспериментах удается достаточно глубоко проникнуть в область метастабильных состояний и приблизиться к спинодали