32

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

ОДЕСЬКИЙ НАЦІОНАЛЬНИЙ ПОЛІТЕХНІЧНИЙ УНІВЕРСИТЕТ

ОДЕСЬКИЙ АВТОМОБІЛЬНО-ДОРОЖНІЙ КОЛЕДЖ

КОНСПЕКТ ЛЕКЦІЙ

з предмету «Вища математика».

Тема: «Лінійна алгебра»

Одеса

2010р.

Склав викладач	Л.П. Юдіна

Рецензент

професор зав. кафедри вищої математики та моделювання систем ОНПУ О.В.. Усов

Розглянуто та узгоджено цикловою

комісією математичних дисциплін

Протокол № __ від « __»_____2010р.

Голова циклової комісії ______ Л.П. Юдіна

ВСТУП

Конспект лекцій з предмету «Вища математика» розроблений у відповідності до робочої програми з вищої математики для спеціальностей «Бухгалтерський облік», «Економіка підприємства», «Організація та управління на автотранспорті», а також може бути використана для інших спеціальностей.

Він містить теоретичний матеріал та розібрані приклади задач з тем «Матриці та визначники» і «Системи лінійних алгебраїчних рівнянь». Ця методична розробка може бути використана як викладачами так і студентами.

У відповідності до неї складений збірник завдань з цих тем.

1. Матриці та визначники

1. Різновиди матриць

Означення 1. Матрицею називають таблицю упорядкованих чи­сел або будь-яких інших об'єктів, розташованих в m рядках та п стовпцях.

Матриці позначають великими літерами, наприклад А, В, С... та круглими дужками.

Матриця, яка має m рядків та п стовпців, називається матри­цею розміру m п (перший множник завжди вказує кількість рядків). Така матриця має вигляд

Кожен елемент матриці А має два індекси: перший індекс і вказує номер рядка, в якому знаходиться цей елемент, другий індекс j вказує номер стовпця, який містить цей елемент. Так, елемент знаходиться на перетину другого рядка та третього стовпця матриці А.

Матриця розміру m 1 називається матрицею - стовпцем або вектором-стовпцем. Матриця розміру називається матрицею - рядком або вектором-рядком.

Наприклад, нехай задані матриці.

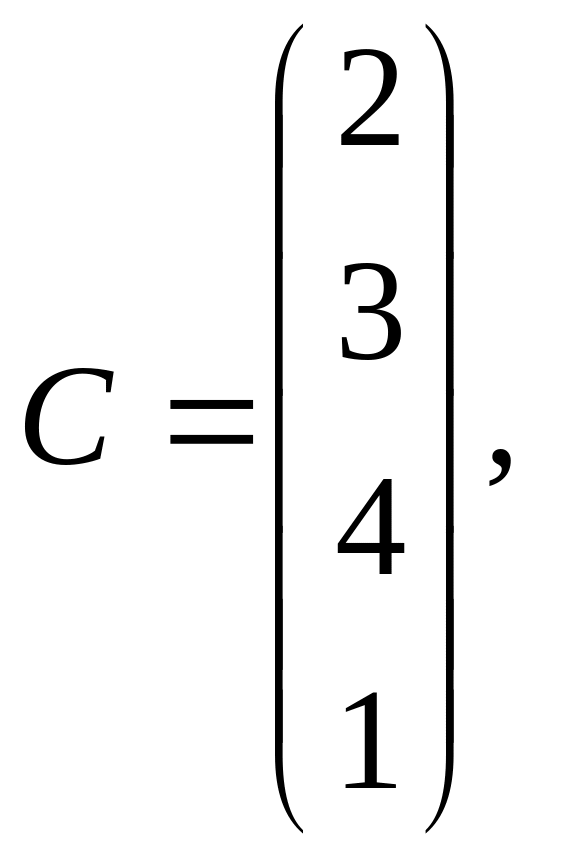
Матриця А має розмір 2 3, матриця В розміру 3 4,

позначається А^Т, а вказана операція перетворення матриці А називається транспонуванням матриці А.

Наприклад, якщо

2. Найпростіші дії з матрицями

Найпростішими діями з матрицями називають множення матриці на число, їх додавання та віднімання, множення матриць.

Добутком матриці А на число k називається матриця, елемен­ти якої дорівнюють добуткам елементів матриці А та числа k:

(1)

Додавати та віднімати можна лише матриці однакового розміру.

Алгебраїчною сумою матриць А та В однакового розміру m п називається матриця С розміру m п, елементи якої c_ij дорівнюють відповідній алгебраїчній сумі елементів a_ij та b_ij матриць А та В, тобто

(2)

Наприклад, якщо тоді

Розглянемо ще один приклад. Якщо матриця F відповідає виробничим параметрам за перший квартал року, а матриця Q , побудована по даним тих же параметрів за другий квартал року, тоді F + Q буде характеризувати ці параметри за перший та другий квартали, тобто за півроку.

Для знаходження добутку АВ матриць А та В необхідно, щоб кількість стовпців матриці А (першого множника) дорівнювала кількості рядків матриці В (другого множника).

Добутком АВ матриці А розміру т n і матриці В розміром п р називається матриця С розміром m , елементи якої дорівнює сумі добутків елементів і-го рядка матриці А на відповідні елементи j-го стовпця матриці В, тобто кожен елемент матриці С знаходиться за формулою

= ( 3 )

Зауваження. Добуток матриць взагалі не має властивості комутативності, тобто АВ ВА. Якщо добуток двох матриць має властивість АВ=ВА, тоді кажуть, що матриці комутують. Наприклад, АЕ=ЕА=А.

_{Приклад 1. Знайти добуток матриць}

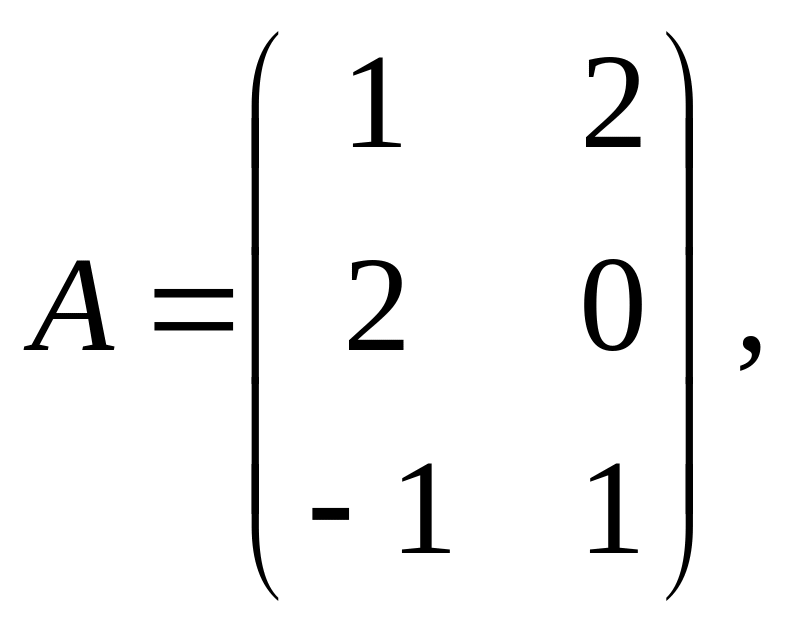
_{Розв’зяування.}

1.3 Визначники

Означення 2. Визначником n-го порядку квадратної числової матриці А по­рядку п називають число, яке знаходиться з елементів матриці А за певним правилом і позначають |А|, або ∆, або det A.

Правило знаходження визначника 2 порядку: визначник другого порядку дорівнює різниці добутків елементів головної та допоміжної діагоналей, тобто

(4)

Приклад 2. Обчислити визначник

Розв'язування. Будемо обчислювати визначник за формулою (4):

Правило знаходження визначника 3-го порядку:

Визначник третього порядку знаходять за формулою

₍₅₎

Кожен доданок у правій частині (5) має 3 множники з різних рядків та стовпців. Три перших доданка із знаком (+) є до­бутками елементів головної діагоналі і елементів вершин трикутників з основами паралельними головній діагоналі (дивись схему малюнок 1 ). Три останні доданки у правій частині (5) мають від'ємний знак. Вони є добутками елементів неголовної діагоналі та елементів вершин трикутників із основами пара­лельними неголовній діагоналі (мал. 1 ).

Мал. 1.

Ця схема обчислення визначника третього порядку називається правилом Саріуса. Існують також інші схеми обчислення виз­начника 3-го порядку.

Приклад 3. Обчислити визначник

Розв'язування. Згідно з формулою (5) одержимо

Для обчислення визначників порядку п > 3 використовують алгебраїчні доповнення.

Означення 3. Мінором M_ij елемента a_ij визначника п-го поряд­ку називається визначник (п - 1) порядку, який одержуємо з ви­значника |А| шляхом викреслювання і-го рядка та j-го стовпця, на перетині яких знаходиться елемент a_ij .

Означення 4. Алгебраїчним доповненням А_ij елемента a_ij визначника називають мінор цього елемента, взятий зі знаком (-1)^i+j , тобто (6)

Приклад 4. Знайти алгебраїчні доповнення до елементів a₂₁ та a₃₃ визначника

Розв'язування. Алгебраїчні доповнення до елементів a₂₁ та a₃₃ позначимо А₂₁ та А₃₃, відповідно. Згідно з означенням 4

; (7)

Мінори M₂₁ та M₃₃ знайдемо згідно з означенням 3:

Підставимо ці значення мінорів у відповідні рівності (7), одержимо шукані алгебраїчні доповнення А₂₁ = -13 та А₃₃ = 5.

Тепер можемо сформулювати правило обчислення визначника п –го порядку.

Правило. Визначник п-го порядку дорівнює сумі добутків усіх еле­ментів будь-якого стовпця (або рядка) на відповідні їм алгеб­раїчні доповнення.

У випадку використання і-го рядка це правило математично можна записати так

(8)

Рівність (8) називають розкладом визначника за елементами і-го рядка. Визначник можна розкласти і за елементами k-го стовпця (k = 1, 2, ..., n).

Отже, обчислення визначника п-го порядку зводиться до об­числення визначників (п - 1) порядку шляхом розкладу визнач­ника за елементами будь-якого рядка або стовпця.

Зауваження. Для скорочення обчислень визначника доцільно його розкласти за елементами такого рядка чи стовпця, який міс­тить найбільшу кількість нулів. У такому випадку не треба знаходити алгебраїчні доповнення до елементів, що дорівнюють 0 (добуток 0 на будь-яке алгебраїчне доповнення дорівнює нулеві).

Таким чином, для ефективного використання методу обчислення визначника шляхом його розкладу за елементами будь-якого рядка або стовпця треба навчитись робити еквівалентні перетворення визначника, які дають можливість одержати нулі у деякому рядку або стовпці.

Виконання таких перетворень здійснюється з використанням властивостей визначника.

Властивості визначників:

1. Визначник при транспонуванні не змінюється.

Доведення

Праві частини рівні, тому і ліві також рівні, тобто

Наслідок. У визначнику рядки та стовпці мають однакові властивості.

2. Якщо у визначнику поміняти місцями будь-які два рядки (стовпці), то визначник змінить знак на протилежний.

Доведення

3. Якщо визначник має два однакових рядки (стовпця), то він дорівнює нулю.

Дійсно, якщо ми поміняємо місцями рівні рядки (стовпці), то визначник не зміниться, але згідно властивості 2 він повинен змінити знак на протилежний. Тому визначник повинен дорівнювати 0.

4. Якщо у визначнику усі елементи одного рядка (стовпця) по­множити на однакове дійсне число k, то визначник зросте також в k разів.

Доведення

Наслідок 1. Спільний множник усіх елементів будь-якого рядка (стовпця) визначника можна винести за знак визначника.

Наслідок 2. Якщо усі елементи будь-якого рядка (стовпця) ви­значника дорівнюють нулю, то визначник дорівнює нулю

5. Визначник, у якого відповідні елементи двох будь-яких рядків (стовпців) пропорційні, дорівнює нулю. Доведення цієї властивості випливає з властивостей 3 та 4.

6. Якщо до всіх елементів будь-якого рядка (стовпця) ви­значника додати відповідні елементи іншого рядка (стовпця) цього визначника, помножені на одне й те ж саме число, то визначник не зміниться.

Доведення

Приклад 5. Обчислити визначник

Розв’язання. У цьому визначнику елементи другого рядка мають спільний множник 2, а елементи четвертого рядка - спільний множник 3. Винесемо ці множники за знак визначника:

У першому рядку зробимо всі елементи, крім останнього, нулями. Для цього до першого стовпика додамо четвертий, помножений на -5, до другого - четвертий, помножений на 2, до третього - четвертий, помножений на -3. Матимемо:

_{Розкладемо останній визначник за елементами першого рядка:}

_{У другому стовпчику -9 замінюємо на 0. Для цього до другого рядка додамо третій, помножений на 9.}

_{Розкладемо останній визначник за елементами другого стовпчика:}