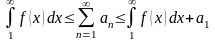- •1.Пространство rⁿ
- •2.Метрическое пространство, евклидово пространство.
- •3.Основные или важнейшие множества точек пространства
- •3.Функции n-переменных.
- •4.Сходимость в пространтсве Rn.
- •6.Предел функции нескольких переменных.
- •8.Повторные пределы.
- •9.Непрерывность функции нескольких переменных.
- •10.Непрерывность функции нескольких
- •11. Основрые свойства непрерывных функций нескольких переменных
- •12. Частные производные ф-ии нескольких переменных
- •13. Дифференцируемость ф-ии нескольких переменных
- •14. Дифференциал функции нескольких переменных
- •15. Достаточное условие дифференцируемости ф-ии нескольких переменных
- •16. Дифференцирование сложной ф-ии
- •17. Однородная функция. Теорема эйлера об однородных функциях
- •18. Инвариантность формы первого дифференциала функции нескольких переменных
- •19. Геометрический смысл дифференциуемости функции двух переменных
- •20. Производная по направлению
- •22.Частные производные высшего порядка.
- •23.Теорема о равенстве смешанных производных второго порядка ф-ции двух переменных.
- •24.Производные высших порядков.
- •27. Экстремум функции многих переменных.
- •28.Достаточные услов локальн экстрем ф-ций нескол перемен.
- •28. Критерий Сильвестра
- •29.Определение наибольшего и наименьшего значения
- •30.Не явные ф-ции.
- •31.Вычисление частных производн неявно заданных ф-ций.
- •32.Неявные ф-ции определ систем функцион уравнений.
- •33. Зависимость ф-и нескольких переменных
- •34.Функциональные матрици
- •35. Усл.Экстремум
- •36.Метод неопредёлённых множетелей Логранжа.
- •37.Числовой ряд. Сходимость, расходимость рядов.
- •38.Необход признак сходим ряда.
- •39. Признак сравнения рядов
- •40.Признак Даламбера.
- •41.Признак Коши.
- •42. Интегральный признак Коши
- •43. Признак Лейбница
- •44. Абсолютная сходимость рядов
- •45. Признаки Дирихле и Абеля
- •47.Функциональные последовательности и ряды.
- •48.Равномерная сходимость функциональных рядов.
- •49.Свойства равном сходящ функции рядов.
- •50.Степенные ряды.
- •55.Ряд Фурье для четн. И нечетн. Ф-ий:
- •56.Ряд Фурье для ф-ций заданных на отрезке .
36.Метод неопредёлённых множетелей Логранжа.
Пусть
треб н-ти экстрем ф-ции u=f(x1..xn, y1..ym) при
налич услов связи Fi(x1..xn, y1..ym)=0 состав
ф-цию:
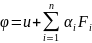 эту ф-цию наз ф-цией Лагранжа счит что
для
эту ф-цию наз ф-цией Лагранжа счит что
для
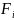 вып все услов сформулир ранее и что
ф-ция u дифференц, выберем множет
вып все услов сформулир ранее и что
ф-ция u дифференц, выберем множет
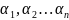 так чтобы выполн равенст:
так чтобы выполн равенст: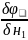 =0,
=0,
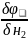 =0,
=0,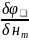 =0,
=0,
Это
можно сдел т.к. эти рав прив к систем
линейн уравнен: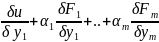 =0…
=0…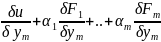 =0
определ которой:
=0
определ которой: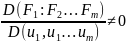 ,
потому дифференц ф-ции: d
,
потому дифференц ф-ции: d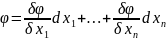 +
+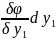 +…+
+…+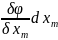 =
=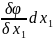 +..+
+..+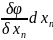 т.к. при сдел предпол перемен x1..xn явл
независ то отсюда:
т.к. при сдел предпол перемен x1..xn явл
независ то отсюда:
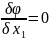 ,
,
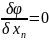 в резул для нах условн экстрем получ
сист n+2m уравн:
…
– n-уравн;
в резул для нах условн экстрем получ
сист n+2m уравн:
…
– n-уравн;
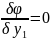 …
…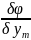 =0
– m-уравн;
=0
– m-уравн;
F1=0…Fm=0
–m- уравн.(*) решая эту ситем найд коорд
точек возможн экстрем и множет: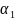 …
…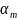 .
Предпол что в М0 вып необх услов условн
экстрем.Пусть ф-ции u1, F1,F2…Fm дважды
диференц в окрестн точки М0 и все частн
произв 2-го порядка непрер в М0. Из
построен ф-ции Лагранжа видно что при
нал услов связи (2) экстрем ф-ции u и ф-ции
Лагранжа совпад поэт для получ достат
услов в точке М0 ф-ци u при нал связей
след присоед к услов сис уравн (*), требов
знака определ в этой точке
.
Предпол что в М0 вып необх услов условн
экстрем.Пусть ф-ции u1, F1,F2…Fm дважды
диференц в окрестн точки М0 и все частн
произв 2-го порядка непрер в М0. Из
построен ф-ции Лагранжа видно что при
нал услов связи (2) экстрем ф-ции u и ф-ции
Лагранжа совпад поэт для получ достат
услов в точке М0 ф-ци u при нал связей
след присоед к услов сис уравн (*), требов
знака определ в этой точке
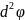 при этом в точке М0 будет минимум если
при налич связей:
при этом в точке М0 будет минимум если
при налич связей: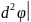 М0>0
услов min;
М0<0-max.
Замеч: второй дифференц
М0
можно вычисл так как если бы все перемен
x1..xn, y1..ym были незав в этом случ:
=(
М0>0
услов min;
М0<0-max.
Замеч: второй дифференц
М0
можно вычисл так как если бы все перемен
x1..xn, y1..ym были незав в этом случ:
=(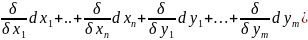 2
..
2
..
37.Числовой ряд. Сходимость, расходимость рядов.
Пусть
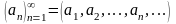 –
–
числовая последовательность. Выражение вида
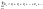
называется числовым рядом, числа
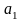 ,
,
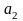 ,
…,
,
…,
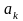 ,
… – членами ряда, а
,
… – членами ряда, а
число
–
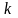 -м
или общим членом ряда.
-м
или общим членом ряда.
Сумма
конечного числа
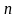 первых членов
первых членов
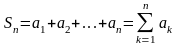
называется -й частичной суммой данного ряда.
В частности,
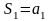 ,
,
 ,
,
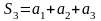 ,
,
……………………
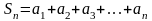
Если
для последовательности
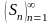
частичных
сумм ряда
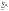 существует
существует
конечный
предел
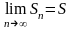 ,
то ряд
,
то ряд
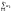 называется
сходящимся, а число
называется
сходящимся, а число
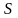 – суммой
данного ряда:
– суммой
данного ряда:
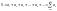 .
.
Если предел последовательности
не существует или равен бесконечности,
то ряд называют расходящимся.
38.Необход признак сходим ряда.
Теор:
если ряд
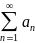 сход, то его n-член стрем к 0, при n
сход, то его n-член стрем к 0, при n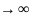 ,
тоесть
,
тоесть
 =0.Д-во:
рассмотр частичн суммы данного ряда:
Sn-1=a1+a2+..+an-1;
=0.Д-во:
рассмотр частичн суммы данного ряда:
Sn-1=a1+a2+..+an-1;
Sn-=a1+a2+..+an-1+an
т.к.
ряд
сход
то
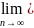 Sn-1=
Sn-=S ,т.к.
an= Sn= Sn-1, то
=
(Sn- Sn-1)=S-S=0. Следств:
n-член ряда не стрем к нулю при n
,
то ряд расход:
Sn-1=
Sn-=S ,т.к.
an= Sn= Sn-1, то
=
(Sn- Sn-1)=S-S=0. Следств:
n-член ряда не стрем к нулю при n
,
то ряд расход: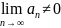 .
Расм ряд вида:
.
Расм ряд вида:
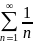 =1+
=1+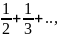 an=
an=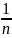 ,
,
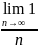 =0,
то данный ряд расход предпол что данный
ряд сход, тоесть:
Sn=S,
S2n=S,
S2n-
Sn)=0 однако: S2n- Sn=
=0,
то данный ряд расход предпол что данный
ряд сход, тоесть:
Sn=S,
S2n=S,
S2n-
Sn)=0 однако: S2n- Sn=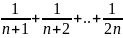 >
> n=
n=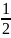 получ против, следов данный ряд расход,
этот ряд наз гармоническим.
получ против, следов данный ряд расход,
этот ряд наз гармоническим.
39. Признак сравнения рядов
(признак Дирихле) Пусть
1)
последовательность
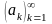 монотонна и
монотонна и
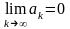 ,2)
последовательность сумм
,2)
последовательность сумм
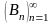 ,
,
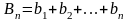 ,
ограничена. Тогда ряд
,
ограничена. Тогда ряд
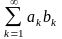 сходится.
сходится.
(признак Абеля) Пусть
1)
последовательность
ограничена и монотонна, 2) ряд
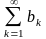 сходится. Тогда ряд
сходится.
сходится. Тогда ряд
сходится.
(признак
Коши) Пусть для ряда
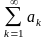 (
(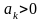 )
существует предел
)
существует предел
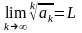 .
Тогда при
.
Тогда при
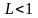 ряд
сходится, а при
ряд
сходится, а при
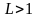 ряд
расходится.
ряд
расходится.
(признак
сравнения) Пусть для членов рядов
и
справедливо неравенство
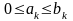
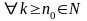 .
Тогда:1) если ряд
сходится, то и ряд
сходится, 2) если ряд
расходится, то и ряд
расходится
.
Тогда:1) если ряд
сходится, то и ряд
сходится, 2) если ряд
расходится, то и ряд
расходится
(интегральный
признак Коши) Если неотрицательная
интегрируемая функция
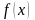 на промежутке
на промежутке
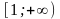 монотонно убывает, и члены ряда
имеют вид
монотонно убывает, и члены ряда
имеют вид
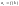 ,
то ряд
и несобственный интеграл
,
то ряд
и несобственный интеграл
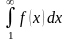 сходятся или расходятся одновременно,
причем в случае сходимости имеет место
неравенство:
сходятся или расходятся одновременно,
причем в случае сходимости имеет место
неравенство: