1 Основная задача радиоэлектроники состоит в разработке и исследовании методов и устройств для передачи, приёма и обработки информации с помощью электрических сигналов и электромагнитных волн. В этом определении ключевым является понятие информации. Количественная оценка информации основывается на концепции выбора наиболее важного сообщения из всей совокупности возможных сообщений. При этом чем менее вероятен выбор данного сообщения, то есть, чем более оно неожиданно для получателя, тем большее количество информации в нем содержится. Общая формула для определения количества информации, содержащегося в сообщении , выглядит так:

(1.1)

где - вероятность появления данного сообщения.

Последовательность преобразований при передаче информации выглядит следующим образом:

Информация  Сообщение  Сигнал

В широком смысле сигналом называют процесс изменения во времени физического состояния какого-либо объекта, служащий для отображения, регистрации и передачи сообщений. По своей физической природе сигналы могут быть световыми, звуковыми, электрическими. Практически любую физическую величину можно преобразовать в пропорциональную ей электрическую величину (обычно напряжение). Такие преобразования осуществляются первичными преобразователями (датчиками). Далее электрический сигнал обрабатывается радиоэлектронными цепями и устройствами и при необходимости может быть передан на расстояние по проводам или с помощью электромагнитных волн. Если носителем сообщения является электрическое напряжение или ток, сигнал называется электрическим, если электромагнитная волна – радиосигналом.

По математическому представлению все электрические сигналы могут быть разделены на детерминированные и случайные.

Детерминированным называют сигнал, который может быть точно задан в виде некоторой аналитической функции времени. Значения детерминированного сигнала в любой момент времени полностью известны и могут быть предсказаны с вероятностью, равной единице. Одним из примеров детерминированного сигнала является гармонический сигнал

, (1.2)

где: - амплитуда сигнала; - круговая частота; - начальная фаза.

С точки зрения теории информации детерминированные сигналы не несут никакой информации. Если заранее известно математическое описание такого колебания, то его можно передать одним кодовым знаком или создать его в точке приема без канала связи. Детерминированные сигналы представляют собой удобную математическую модель и используются для анализа работы радиоэлектронных цепей и устройств. Гармонический сигнал является также периодическим сигналом, поскольку повторяется во времени с периодом . Наряду с периодическими сигналами в радиоэлектронике используются и непериодические сигналы.

Случайным называют сигнал, характер изменения которого невозможно достоверно предсказать (рис. 1.1).

Рис.1.1. Реализация случайного сигнала

Примерами случайных сигналов являются электрические напряжения, полученные в результате преобразования речи, музыки, изображения, а также шумы на выходе радиоэлектронных устройств, электрические импульсы, сопровождающие грозовые разряды, индустриальные радиопомехи. Все сигналы, несущие информацию, также являются случайными. Так сигнал на выходе приемника радиотелескопа, направленного на источник космического излучения, представляет собой хаотические электрические колебания, несущие разнообразную информацию о природном объекте. Временная функция случайного сигнала неизвестна, можно оценить лишь некоторые его вероятностные характеристики. Статистическая радиотехника для анализа свойств случайных сигналов использует математический аппарат теории вероятностей и теории случайных процессов. Использование теории вероятностей для анализа физических процессов в радиоэлектронных цепях нежелательно ввиду сложности математического аппарата вероятностных расчётов. Из соображений простоты и наглядности анализа рассматривают работу радиоэлектронных устройств при воздействии детерминированных сигналов. При этом для учёта случайного характера реального сигнала в качестве его математической модели используют не отдельную детерминированную функцию , а множество однотипных детерминированных функций , образующее в совокупности некоторый случайный процесс, в котором уже будет содержаться информация.

Важный класс сигналов в радиоэлектронике представляют импульсные сигналы, то есть электрические колебания, существующие в пределах конечного отрезка времени. При этом различают видеоимпульсы (рис. 1.2 а) и радиоимпульсы(рис. 1.2 б).

аб

Рис.1.2. Видеоимпульс (а) и радиоимпульс (б)

Происхождение термина «видеоимпульс» связано с тем, что впервые такие сигналы стали применяться в технике телевидения. Если - видеоимпульс, то соответствующий ему радиоимпульс Огибающей радиоимпульса является видеоимпульс . Функция называется высокочастотным заполнением.

К радиосигналам относятся модулированные сигналы – высокочастотные колебания, один или несколько параметров которых изменяются по закону низкочастотного модулирующего напряжения (рис. 1.3). При этом используется амплитудная, частотная, фазовая, импульсная и ряд других более сложных видов модуляции.

Рис.1.3. Амплитудно-модулированный сигнал

Электрические сигналы могут быть аналоговыми и дискретными. Поскольку аналоговые сигналы обычно являются выходными сигналами датчиков физических величин и повторяют закон изменения соответствующей физической величины, их иногда называют непрерывными сигналами (рис. 1.4). Первоначально в радиотехнике использовались только аналоговые сигналы, с помощью которых успешно решались задачи радиосвязи и телевидения. Впоследствии с появлением импульсных радиотехнических систем стали использоваться дискретные сигналы. Дискретныесигналы представляют собой последовательность импульсов, амплитуды которых соответствуют значениям физической величины в дискретные моменты времени (рис.1.5). Дискретныйсигнал в заданном интервале амплитуд может принимать только определённые значения, заранее обусловленные.

Поскольку между дискретными значениями сигнала остаетсянезаполненный передачей интервал времени, появляется возможность по одной и той же радиолинии передавать сообщения от разных источников, организуя многоканальную связь с разделением каналов по времени.

Одной из разновидностей дискретных сигналов являются цифровые сигналы (рис. 1.6). Дискретные во времени и квантованные по уровню сигналы, являющиеся последовательностью импульсов, амплитуды которых могут принимать только ограниченное число фиксированных значений, называются цифровымисигналами. Последовательные отсчеты цифровых сигналов представляются числами в двоичном коде.

1.6. Цифровые сигналы

Цифровые сигналы получают из аналоговых сигналов на выходе специальных устройств, называемых аналого-цифровыми преобразователями (АЦП). АЦП осуществляют дискретизацию аналогового сигнала во времени и квантование последовательных дискретных отсчетов по уровню. Цифровые сигналы связаны с работой цифровых интегральных схем, используемых в микроэлектронике.

Аналитическая функция времени, представляющая математическую модель электрического сигнала, наиболее полно описывает сигнал, что не всегда требуется. Часто достаточно знать ряд обобщённых физических параметров таких, как длительность сигнала, динамический диапазон, ширина спектра. Ниже на рис. 1.7 приведены некоторые параметры импульсных сигналов.

Длительность сигнала – это интервал времени, в пределах которого существует сигнал. Длительность импульсного сигнала принято оценивать на уровне половины от его высоты.

Рис.1.7. Параметры импульсного сигнала

Длительность фронта – это время нарастания сигнала от уровня 0,1 до уровня 0,9 его амплитуды .

Длительность спада – это время изменения сигнала от уровня 0,9 до уровня 0,1 его амплитуды.

Ширина спектра характеризует скорость изменения сигнала и полосу частот сигнала. Спектр некоторых сигналов может быть неограниченным, однако для любого сигнала можно указать диапазон частот, в пределах которого сосредоточена его основная энергия. Этим диапазоном и определяется ширина спектра сигнала.

Одним из параметров периодических прямоугольных импульсов является скважность импульсов, равная отношению периода следования импульсов к длительности импульса:

. (1.3)В теории сигналов используется такой параметр как база сигнала

, (1.4) где: - ширина спектра; - длительность сигнала.

Важной характеристикой сигнала является его энергия. Величина

(1.5)называется нормой сигнала на интервале . Квадрат нормы равен энергии сигнала

. (1.6)

2

Дискретное представление сигналов. Теорема отсчетов

Аналоговые сигналы в заданном диапазоне амплитуд принимают все значения и описываются непрерывными функциями времени. В соответствии с теоремой отсчетов аналоговый сигнал с ограниченным спектром полностью определяется своими дискретными значениями, взятыми через интервалы времени

, (1.13)

где – верхняя граничная частота в спектре сигнала.

Смысл теоремы в том, что для передачи по каналу связи непрерывного сигнала нет необходимости передавать все бесчисленное множество его значений, достаточно передать его отдельные мгновенные значения, отсчитанные через интервалы . По этим значениям функция может быть восстановлена на приёмном пункте единственным образом.

В соответствии с теоремой отсчетов функция s(t), описывающая аналоговый сигнал, может быть разложена в ряд вида:

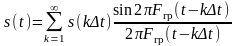_, (1.14)

где:

– значения дискретных отсчётов функции в моменты времени ;

- базисные ортогональные функции.

Представление непрерывного сигнала в соответствии с теоремой отсчетов показано на рис. 1.11.

Рис. 1.11. Представление непрерывного сигнала по теореме отсчетов

В соответствии с рис. 1.11 непрерывную функцию можно представить в виде суммы дельта-импульсов, соответствующих моментам времени , умноженных на значения функции в эти моменты времени и пропущенных через идеальный фильтр нижних частот с граничной частотой . Напряжение на выходе такого фильтра при подаче на вход дельта-импульса в момент времени соответствует его импульсной характеристике

. (1.15)

Исходный непрерывный сигнал будет восстановлен после прохождения через фильтр всех дискретных отсчетов сигнала в результате суммирования функций .

На практике не существует сигналов с ограниченным спектром, так как все сигналы, ограниченные во времени, имеют бесконечную ширину спектра. Не существует также и идеальных фильтров. Поэтому исходный сигнал восстанавливается с некоторой погрешностью. При несоблюдении частоты дискретизации возможно наложение спектров дискретизированного сигнала.

В литературе эта теорема известна как теорема отсчетов Уиттакера-Найквиста -Шеннона-Котельникова.

Временной метод анализа сигналов

Суммируя по всем элементарным скачкам на интервале существования сигнала, и, переходя от суммы к интегралу, получим результирующее напряжение на выходе линейной цепи:

. (2.2)

Это соотношение известно как интеграл свертки или интеграл Дюамеля.

Сигналы на входе и выходе линейной цепи Таблица 2.1

Воздействие на входе линейной цепи
Отклик на выходе линейной цепи

результирующее напряжение на выходе линейной цепи будет равно:

. (2.5)

Последнее выражение носит название интеграла Дюамеля в импульсной форме.

Этот интеграл является интегралом свертки двух функций и Импульсная характеристика линейной цепи связана преобразованиями Фурье с комплексным коэффициентом передачи линейной цепи следующим образом:

, (2.6)

. (2.7)

3

Единичный скачок. Единичный импульс.

Одной из задач радиоэлектроники является анализ прохождения электрических сигналов через линейные цепи. Зная форму входного и выходного сигналов, можно оценить свойства линейной цепи.

Линейной называется электрическая цепь, к которой применим принцип суперпозиции. В теоретическом курсе радиоэлектроники часто для упрощения анализа используют различного рода идеализации. В частности, для теоретического анализа воздействия детерминированных сигналов на линейные цепи используют математические модели идеальных электрических сигналов. Одним из таких сигналов является единичный скачок(рис.1.8).

Рис. 1.8. Единичный скачок

Единичный скачок, описывается функцией вида:

(1.7) Эту функцию называют функцией включения. Впервые эту функцию ввел английский физик Оливер Хевисайд (1850 - 1925). Реальный аналоговый сигнал можно приближенно представить некоторой суммой единичных скачков, возникающих в последовательные моменты времени. Устремив к нулю длительность интервала времени между единичными скачками, в пределе будет получена точная огибающая реального исходного сигнала. Такой способ представления сигналов называется динамическим (рис. 1.9).

Рис. 1.9. Динамическое представление сигнала с помощью единичных скачков

Если на вход линейной цепи подать напряжение в виде единичного скачка , то изменение напряжения во времени на выходе цепи будет представлять ее переходную характеристику Единичный скачок является хорошим тестовым сигналом для исследования переходных характеристик линейных цепей. Поскольку единичный скачок является лишь математической моделью, которую экспериментально реализовать не представляется возможным, то при практическом исследовании линейных цепей используют периодические прямоугольные импульсы, анализируя реакцию линейной цепи на фронты и спады импульсов, которые условно можно считать единичными скачками противоположных знаков.

Другой способ представления реального сигнала использует математическую модель идеализированного сигнала в виде единичного импульса или дельта-импульса (-импульса) (рис. 1.10). В математической физике его еще называют функцией Дирака.

Рис. 1.10. Единичный импульс

Аналитически эта функция записывается следующим образом:

(1.8)

Кроме того:

. (1.9)

Отсюда следует связь между единичным скачком и единичным импульсом:

. (1.10)

Если на вход линейной цепи подать напряжение в виде единичного импульса, то изменение напряжения во времени на выходе цепи будет представлять собой импульсную характеристику

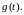
Понятие импульса используется в радиоэлектронике при исследовании воздействия очень коротких импульсов напряжения на линейные цепи. При этом не обязательно, чтобы длительность реального сигнала была бесконечно мала, а амплитуда бесконечно велика. Достаточным является условие, чтобы длительность импульса была много меньше постоянной времени цепи.

Реальный сигнал можно представить некоторой суммой единичных импульсов, возникающих в последовательные моменты времени. Эти импульсы примыкают непосредственно друг к другу и вписываются в огибающую исходного сигнала.

-импульс обладает стробирующим свойством. Стробирование – получение значения сигнала в заданный момент времени.

Рассмотрим - импульс, сдвинутый по оси времени на :

(1.11)

Для некоторой непрерывной функции можно записать:

. (1.12)

Последнее выражение получено, исходя из того, что функция равна нулю везде, кроме точки . Стробирующее свойство функции используется в аналого-цифровых преобразователях при дискретизации сигналов.

4

СПЕКТРАЛЬНЫЙ АНАЛИЗ ПЕРИОДИЧЕСКИХ СИГНАЛОВ

В соответствии со спектральным способом анализа прохождения сигналов через линейные цепи любой случайный сигнал s(t) можно представить в виде бесконечной суммы элементарных аналитически однотипных детерминированных сигналов :

Подавая на вход линейной цепи (рис. 1.14), коэффициент передачи которой равен , элементарный детерминированный сигнал, можно найти элементарный отклик цепи, то есть сигнал на выходе цепи.

Рис.2.3.К определению сигнала на выходе линейной цепи.

Сигнал на выходе линейной цепи равен

(2.9)

Поскольку для линейных цепей справедлив принцип суперпозиции, то результирующий отклик будет равен:

(2.10)

Функции, описывающие элементарные сигналы, называются базисными функциями. Представление сигнала базисными функциями упрощается, если они являются ортогональными и ортонормированными.

Набор функций называется ортогональным, если в интервале от до

при (2.11)

и ортонормированным, если для всех выполняется условие

. (2.12)

Ортогональность базисных функций, с помощью которых представляется исходный сигнал , является гарантией того, что представление сигнала может быть сделано единственным образом. Условию ортогональности отвечают гармонические функции кратных частот, а также функции Уолша, которые на отрезке своего существования от до принимают лишь значения, равные 1, дискретные сигналы Баркера и некоторые другие функции. Спектральный метод анализа сигналов основан на преобразованиях Фурье и состоит в замене сложной функции времени, описывающей сигнал, суммой простых гармонических сигналов, образующих частотный спектр этого сигнала. Знаменитый французский физик и математик Ж. Б. Фурье (1768 – 1830 г.г.) доказал, что любое изменение во времени некоторой функции можно аппроксимировать в виде конечной или бесконечной суммы ряда гармонических колебаний с разными амплитудами, частотами и начальными фазами. Этой функцией может быть ток или напряжение в электрической цепи.

Рассмотрим вначале представление периодического электрического сигнала (рис. 2.4), отвечающего условию

, (2.13)

где: - период сигнала; =1,2,3,….

Рис. 2.4.Периодический сигнал

Представим этот сигнал бесконечным тригонометрическим рядом:

. (2.14)

Этот ряд называется рядом Фурье.

Возможна запись ряда Фурье в другом виде:

, (2.15)

где: - модуль амплитуд гармоник;

- фазы гармоник;

- круговая частота;

- коэффициенты косинусоидальных составляющих; - коэффициенты синусоидальных составляющих; - среднее значение сигнала за период (постоянная составляющая).

Отдельные слагаемые рядов называют гармониками. Число является номером гармоники.Совокупность величин в ряде (2.15) называют спектром амплитуд, а совокупность величин - спектром фаз.

Ниже на рис. 2.5 представлены амплитудный и фазовый спектры периодического сигнала. Вертикальные отрезки амплитудного спектра представляют амплитуды гармоник и называются спектральными линиями.

Рис 2.5. Амплитудный и фазовый спектры периодического сигнала

Таким образом, спектр периодического сигнала – линейчатый.Каждый периодический сигнал имеет вполне определенные амплитудный и фазовый спектры.

Сумма ряда (2.15) является бесконечной, но, начиная с некоторого номера, амплитуды гармоник настолько малы, что ими можно пренебречь и практически реальный периодический сигнал представляется функцией с ограниченным спектром. Интервал частот, соответствующий ограниченному спектру, называется шириной спектра.

Если функция , описывающая периодический сигнал, является четной, то сумма ряда (2.14) будет содержать только косинусоидальные составляющие. Если - нечетная функция, то сумма будет содержать только синусоидальные составляющие.

Возможно также представление периодического сигнала в виде комплексного ряда Фурье:

, (2.16)

где:

- комплексные амплитуды спектра, содержащие информацию, как об амплитудном, так и о фазовом спектрах.

После подстановки значений и , получим:

(2.17)

Если подставить полученное значение в ряд (1.29), то он обращается в тождество. Таким образом, периодический электрический сигнал можно задавать либо функцией времени , либо комплексной амплитудой спектра.

Спектр периодической последовательности прямоугольных импульсов

Состав спектра периодической последовательности прямоугольных импульсов зависит от величины отношения периода последовательности к длительности импульса, называемого скважностью импульсов. В спектре будут отсутствовать гармоники с номерами кратными скважности импульсов. Скважность импульсов равна . На рис.1.17 приведены три импульсные последовательности с разными скважностями и соответствующие им спектры. Для периодической последовательности, скважность которой равна 2, в спектре отсутствуют 2, 4, 6 ,8 и т.д. гармоники. Для последовательности, скважность которой равна 3, в спектре отсутствуют 3, 6 и т.д. гармоники. Для последовательности, скважность которой равна 4, в спектре отсутствуют 4, 8 и т.д. гармоники. Во всех приведенных спектрах интервал между спектральными линиями равен величине обратной периоду последовательности. Точки на оси частот, в которых спектр равен нулю, соответствуют величине, обратной длительности импульсов периодических последовательностей.

Рис.2.6.Периодические последовательности импульсов и их спектры.

5

Спектр непериодического сигнала

При рассмотрении спектра непериодического сигнала воспользуемся предельным переходом от периодического сигнала к непериодическому сигналу, устремив период к бесконечности.

Для периодического сигнала, представленного на рис. 2.4, ранее получено выражение (2.17) для комплексной амплитуды спектра:

(2.18)

Введем обозначение:

(2.19)

Построим модуль спектра :

Рис. 2.7. Модуль спектра периодического сигнала

Расстояние между спектральными линиями равно . Если увеличивать период , то будет уменьшаться интервал ₁ . При интервал между спектральными линиями ₁d. При этом периодическая последовательность импульсов превращается в одиночный импульс и модуль спектра стремится к непрерывной функции частоты . В результате предельного перехода от периодического сигнала к непериодическомулинейчатый спектр вырождается в сплошной спектр, представленный на рис. 2.8.

Рис. 2.8. Спектр непериодического сигнала

При этом комплексная амплитуда равна:

. (2.20)

С учетом предельного перехода при

(2.21)

Подставим полученное выражение в ряд (2.16). При этом сумма трансформируется в интеграл, а значения дискретных частот в значение текущей частоты и непериодический сигнал можно представить в следующем виде:

. (2.22)

Это выражение соответствует обратному преобразованию Фурье. Огибающая сплошного спектра одиночного импульса совпадает с огибающей линейчатого спектра периодической функции, представляющей периодическое повторение этого импульса.

Интеграл Фурье позволяет любую непериодическую функцию представить в виде суммы бесконечного числа синусоидальных колебаний с бесконечно малыми амплитудами 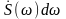и бесконечно малым интервалом по частоте.Спектр сигнала определяется из выражения

. (2.23)

Этот интеграл соответствует прямому преобразованию Фурье.

– комплексный спектр, в нём содержится информация, как о спектре амплитуд, так и о спектре фаз.

Таким образом, спектр непериодической функции сплошной. Можно сказать, что в нём содержатся «все» частоты. Если вырезать из сплошного спектра малый интервал частот , то частоты спектральных составляющих в этом участке будут отличаться сколь угодно мало. Поэтому спектральные составляющие можно складывать так, как будто все они имеют одну и ту же частоту и одинаковые комплексные амплитуды. Спектральная плотность есть отношение комплексной амплитуды малого интервала частот к величине этого интервала.

Спектральный анализ сигналов имеет фундаментальное значение в радиоэлектронике. Информация о спектре сигнала позволяет обоснованно выбирать полосу пропускания устройств, на которые воздействует этот сигнал.

Спектр одиночного прямоугольного видеоимпульса

Рассчитаем спектр одиночного прямоугольного импульса, амплитуда которого равнаЕ, а длительность - , представленного на рис. 2.9.

Рис. 2.9. Одиночный прямоугольный импульс

В соответствии с выражением (2.24) спектр такого сигнала равен

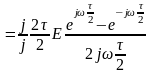= . (2.24)

Поскольку 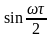= 0 , когда , то частоты, на которых спектр обращается в нуль равны , где k=1,2,3…

На рис. 2.10 представлен комплексный спектр одиночного прямоугольного импульса длительностью .

Рис.2.10. Спектр одиночного прямоугольного импульса

Спектральная плотность определяет распределение энергии в спектре одиночного импульса. В общем случае распределение энергии неоднородно. Однородное распределение характерно для хаотического процесса, называемого «белым шумом».

Спектральная плотность импульса на нулевой частоте равна его площади. Приблизительно 90% энергии одиночного прямоугольного импульса сосредоточено в спектре, ширина которого определяется выражением

. (2.25)

Соотношение (1.41) определяет требования к ширине полосы пропускания радиотехнического устройства. В задачах, где форма сигнала имеет второстепенное значение полосу пропускания устройства для этого сигнала можно выбрать равной ширине первого лепестка спектра. При этом неизвестна степень искажения формы сигнала. Двукратное увеличение полосы пропускания лишь на 5% увеличит энергию сигнала при одновременном возрастании уровня шумов.

7

ЭЛЕМЕНТЫ РАДИОЭЛЕКТРОННЫХ СХЕМ.

Радиоэлектронные цепи и устройства состоят из пассивных и активных элементов. Пассивными элементами являются резисторы, катушки индуктивности и конденсаторы. Сопротивление элементов электрической цепи току может быть двух видов – активное и реактивное. Если при прохождении тока по цепи происходят необратимые затраты электрической энергии, то сопротивление цепи называется активным. Если же подобной затраты нет, сопротивление называется реактивным. К активным сопротивлениям относятся резисторы, а к реактивным сопротивлениям – катушки индуктивности и конденсаторы. В действительности не существует чисто активных и реактивных сопротивлений. Такая терминология является следствием идеализации, так как любая катушка индуктивности обладает активным сопротивлением. Резистор же на высоких частотах обладает паразитной индуктивностью. Строго говоря, эти элементы нелинейные. Сопротивление, например, зависит от величины протекающего через него тока. Но во многих случаях отклонения от линейности незначительны, и мы вправе им пренебрегать.

Будем считать в последующем анализе резисторы, конденсаторы и катушки индуктивности линейными элементами. Ниже приводятся рисунки пассивных элементов и соответствующие линейные уравнения для токов и напряжений.

Рис.3.1. Пассивные элементы радиоэлектронных схем

К активным элементам относятся источники напряжений и источники токов, биполярные и полевые транзисторы, интегральные микросхемы, электронные лампы, клистроны, магнетроны, лазеры.

Наряду с пассивными и активными элементами в радиоэлектронике широко используются генераторы напряжения и генераторы тока.

Генератором напряжения называется источник напряжение, на выводах которого не зависит от сопротивления нагрузки и, следовательно, от тока нагрузки. Внутреннее сопротивление такого генератора равно

(3.1)

Генератором тока называется источник, ток которого не зависит от сопротивления нагрузки. Внутреннее сопротивление такого генератора равно бесконечности.

Реальные генераторы напряжения и тока отличаются от идеальных тем, что их выходные сигналы – напряжение и ток - зависят от сопротивления нагрузки. Это их свойство можно объяснить тем, что внутренние сопротивление генератора напряжения не равно нулю, а внутреннее сопротивление генератора тока не равно бесконечности. У реального генератора напряжения внутреннее сопротивление должно быть мало по сравнению с сопротивлением нагрузки. У реального генератора тока внутреннее сопротивление должно быть намного больше сопротивления нагрузки.

Линейные цепи – цепи, в которых все элементы линейные, то есть параметры зависят от значений напряжения и тока. Если эти параметры не изменяются во времени, то цепи называются линейными с постоянными параметрами.

такие цепи удовлетворяют принципу суперпозиции, согласно которому реакция линейной цепи на совокупность воздействий равна сумме реакций, вызываемых в той же цепи каждым  воздействием в отдельности. Иными словами, если приложенное напряжение можно представить в виде суммы   слагаемых

                        ,                                (1.3)

 

то возникающий в каком-либо элементе (или участке) цепи ток также будет представлять собой сумму   слагаемых

 

.                             (1.4)

 

8

ДИФФЕРЕНЦИРУЮЩИЕ ЦЕПИ

Сложные радиоэлектронные устройства состоят из простых цепей. Рассмотрим цепь, состоящую из резистора и конденсатора, включенных последовательно с идеальным генератором напряжения, показанную на рис. 3.3.

Рис .3.3. Дифференцирующая цепь

Если выходное напряжение снимается с резистора, то цепь называется дифференцирующей, если с конденсатора – интегрирующей. Эти линейные цепи характеризуются стационарными и переходными характеристиками. Это связано с тем, что изменение величины действующего в цепи напряжения приводит к тому, что токи и напряжения в различных участках цепи приобретают новые значения. Изменение состояния цепи происходит не мгновенно, а в течение некоторого интервала времени. Поэтому различают установившееся и переходное состояние электрической цепи.

Электрические процессы считаются установившимися (стационарными), если закон изменения всех напряжений и токов совпадает с точностью до постоянных величин с законом изменения действующего в цепи напряжения от внешнего источника. В противном случае считают, что цепь находится в переходном (нестационарном) состоянии.

К стационарным характеристикам относятся амплитудно-частотная и фазовая характеристики линейной цепи.

Нестационарное состояние линейной цепи описывается переходной характеристикой.

Будем считать, что к входу цепи подключен идеальный генератор напряжения . На основании второго закона Кирхгофа для дифференцирующей цепи можно записать дифференциальное уравнение, связывающее напряжения и ток в ветвях цепи:

(3.2)

Так как напряжение на выходе цепи , то:

(3.3)

Подставляя в интеграл значение тока, получим:

(3.4)

Продифференцируем левую и правую части последнего уравнения по времени:

(3.5)

Перепишем это уравнение, в следующем виде:

, (3.6)

где =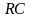 - параметр цепи называемый постоянной времени цепи.

В зависимости от величины постоянной времени возможны два различных соотношения между первым и вторым слагаемыми правой части уравнения.

Если постоянная времени большая по сравнению с периодом гармонических сигналов >> или с длительностью импульсов >> , которые можно подавать на вход этой цепи, то

(3.7)

и напряжение на выходе цепи с небольшими искажениями повторяет входное напряжение:

. (3.8)

Если же постоянная времени мала по сравнению с периодом гармонических сигналов << или с длительностью импульсов << , то

. (3.9)

Отсюда напряжение на выходе равно:

. (3.10)

Таким образом, в зависимости от величины постоянной времени такая -цепь может либо с определенными искажениями передавать входной сигнал на выход, либо с определенной степенью точности его дифференцировать. При этом форма выходного сигнала будет разной. Ниже на рис. 3.4 представлены входное напряжение, напряжения на резисторе и конденсаторе для случаев, когда постоянная времени велика и постоянная времени мала .

аб

Рис. 3.4.Напряжения на элементах дифференцирующей цепи при (а) и (б)

Теперь определим коэффициент передачи дифференцирующей цепи. Комплексный коэффициент передачи дифференцирующей цепи при подаче на вход гармонического сигнала равен:

. (3.11)

Обозначим отношение , где - граничная частота полосы пропускания дифференцирующей цепи.

Выражение для коэффициента передачи примет вид:

. (3.12)

Модуль коэффициента передачи равен:

. (3.13)

- граничная частота полосы пропускания, на которой модуль реактивного сопротивления становится равным величине активного сопротивления, а коэффициент передачи цепи равен 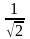. Зависимость модуля коэффициента передачи от частоты называется амплитудно–частотной характеристикой (АЧХ).

Зависимость угла сдвига фаз между выходным и входным напряжениями от частоты называется фазовой характеристикой (ФЧХ). Фазовая характеристика:

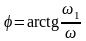(2.14)

Ниже на рис. 3.5 представлены АЧХ и ФЧХ дифференцирующей цепи:

Рис. 3.5.Амплитудно–частотная и фазовая характеристики

дифференцирующей цепи

Из амплитудно-частотной характеристики видно, что прохождение сигналов через дифференцирующую цепь сопровождается уменьшением амплитуд низкочастотных составляющих его спектра. Дифференцирующая цепь является фильтром высоких частот.

Из фазовой характеристики видно, что фазы низкочастотных составляющих сдвигаются на больший угол, чем фазы высокочастотных составляющих.

Переходную характеристику дифференцирующей цепи можно получить, если на вход подать напряжение в виде единичного скачка.

Таким образом, аналитическое выражение для переходной характеристики дифференцирующей цепи записывается в следующем виде:

, (3.21)

На рисунках ниже приведено напряжение единичного скачка и переходная характеристика дифференцирующей цепи.

Рис. 3.6. Единичный скачок и переходная характеристика дифференцирующей цепи

При переходная характеристика .

Постоянная времени - это время, за которое напряжение на выходе дифференцирующей цепи изменяется до уровня 0,37 от начального уровня входного сигнала в виде единичного скачка.

Дифференцирующая цепь укорачивает входные импульсы. Однако дифференцирующие цепи чаще всего применяются не для дифференцирования, а для разделения переменной и постоянной составляющих напряжения. В этом случае постоянную времени цепи берут достаточно большой, чтобы избежать искажений сигнала за счет его дифференцирования.

ИНТЕГРИРУЮЩИЕ ЦЕПИ.

Рис. 3.7. Интегрирующая цепь

На основании второго закона Кирхгофа запишем дифференциальное уравнение для токов и напряжений в интегрирующей цепи:

. (3.22)

Учитывая, что напряжение на выходе

, (3.23)

найдем ток:

. (3.24)

Подставим значение тока в предыдущее уравнение:

(3.25)

В зависимости от величины постоянной времени возможны два различных соотношения между первым и вторым слагаемыми в правой части уравнения (3. 25). Если постоянная времени мала по сравнению с периодом гармонических сигналов << или с длительностью импульсов << , которые можно подавать на вход этой цепи, то

. (3.26)

В этом случае

. (3.27)

Если же постоянная времени большая по сравнению с периодом гармонических сигналов >> или с длительностью импульсов >> , которые можно подавать на вход этой цепи то

. (3.28)

Отсюда

(3.29)

Таким образом, в зависимости от соотношения величины постоянной времени и параметров входных сигналов эта цепь может либо с определенными искажениями передавать входной сигнал на выход, либо с некоторой погрешностью его интегрировать. На рис.3.8 приведены формы импульсов на выходе интегрирующей цепи для различных значений постоянной времени. При цепочка интегрирует входной сигнал, а при цепочка с искажениями передает сигнал на выход.

а б

Рис. 3.8. Напряжения на входе и элементах интегрирующей цепи при (а) и (б).

Считается, что когда цепочка интегрирует.

Определим параметры и характеристики интегрирующей цепи. Коэффициент передачи интегрирующей цепи равен:

(3.30)

Обозначим

, (3.31)

где граничная частота полосы пропусканияинтегрирующей цепи.

Приравняв модуль коэффициента передачи

, (3.32)

найдем граничную частоту

. (3.33)

Модуль коэффициента передачи запишем в следующем виде

(3.34)

Амплитудно-частотная характеристика интегрирующей цепи представляет собой зависимость модуля коэффициента передачи от частоты.

Найдем фазо-частотную (фазовую) характеристику интегрирующей цепи:

(3.35)

На рис. 2.9 приведены амплитудно-частотная и фазовая характеристики интегрирующей цепи.

Рис. 3.9. Амплитудно-частотная и фазовая характеристики интегрирующей цепи

Интегрирующая цепь является фильтром низких частот. При прохождении сигналов через интегрирующую цепь удельный вес высокочастотных составляющих спектра сигнала уменьшается, а фазы этих составляющих сдвигаются на больший угол, чем фазы низкочастотных составляющих.

Таким образом, переходная характеристика интегрирующей цепи

. (3.44)

При

Отсюда следует физический смысл постоянной времени интегрирующей цепи:

- это время, за которое напряжение на выходе интегрирующей цепи изменяется до уровня 0,63 от начального уровня входного напряжения.

Единичный скачок и переходная характеристика интегрирующей цепи представлены на рис. 3.10.

Рис.3.10. Единичный скачок и переходная характеристика интегрирующей цепи

Интегрирующие цепи применяются в ядерной физике для измерения числа импульсов, поступающих на устройство за единицу времени, а также для регистрации слабых сигналов, поступающих на устройство вместе с шумами.