Теорема 1 (Стокса).

Циркуляция векторного поля по контуру равна потоку вихря этого поля через поверхность Σ, натянутую на контур γ, т.е.

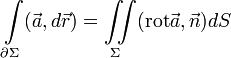
Доказательство.

Докажем теорему Стокса в тех предположениях, которые были сформулированы в начале. Из (1) и (2) получаем уравнения края поверхности

.

Сводя криволинейные интегралы к определенным, получаем

.

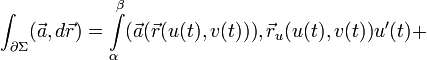
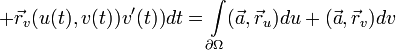Сделаем дополнительное предположение о непрерывности (а следовательно и равенстве) смешанных производных и . Тогда в силу формулы Грина получаем равенство

.

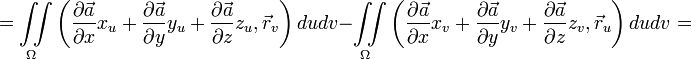
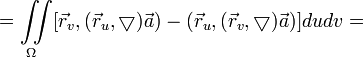
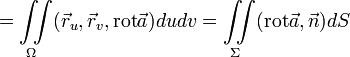Здесь была использована формула

при , а также формула, выражающая поток через двойной интеграл от смешанного произведения:

.

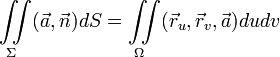Итак, формула Стокса доказана для простой гладкой поверхности, натянутой на кусочно глакий контур.

Билет №17 Теорема о сходимости ряда Фурье в точке.

f - 2π периодическая, абсолютно интегрируемая на отрезке [ − π,π] функция.

x₀ – её почти регулярная точка f.

Тогда ряд Фурье в этой точке x₀ сходится к .

Если же при этом x₀ - регулярная точка f, то ряд Фурье в точке x₀ сходится к f(x₀).

Рассмотрим предел

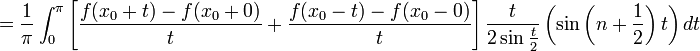
Дробь , доопределенная единицей в нуле, является непрерывной на [ − π,π] функцией.

Дробь абсолютно интегрируема на [ − π,π] функция, поскольку таковой является её числитель, и при она имеет конечный предел.

По теореме Римана об осцилляции, последний интеграл стремиться к нулю при , т.е.

при

Билет №18 Достаточные условия равномерной сходимости тригонометрического ряда Фурье.

Пусть f - 2π периодическя и кусочно непрерывно дифференцируемая функция.

Тогда ряд Фурье функции f сходится к f равномерно на и

при ,

где C не зависит от n.

Доказательство. Пусть 0 < δ = δ_n < π. Перепишем формулу

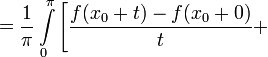
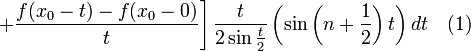
в виде

.

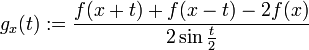Пусть M₁ = max | f' | . C помощью теоремы Лагранжа о конечных приращениях получаем, что при

.

Следовательно, при

и (за исключением быть может, конечного числа значений t)

.

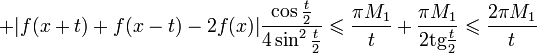Очевидно, что . С помощью интегрирования по частям имеем

.

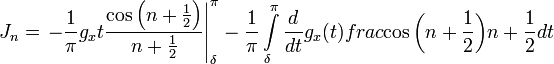Отсюда

, получаем, что при <center> ,

где C не зависит от n. Теорема доказана.

Билет №19 Непрерывность преобразования Фурье абсолютно интегрируемой функции.

Преобразование Фурье абсолютно интегрируемой на функции есть ограниченная и непрерывная на функция.

Доказательство. Так как функция f(x) абсолютно интегрируема на , то

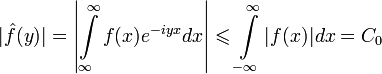
и, следовательно, есть ограниченная функция на .

Для доказательства непрерывности функции запишем её в виде

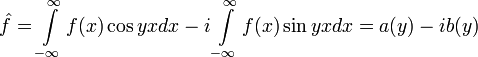
и заметим, что, в силу леммы 4, $74 функция a(y) и b(y) непрерывны на .

Тер-Крикоров А.М., Шабунин М.И. Курс математичсекого анализа. стр.645.

Лемма 4.

Если f(x) - абсолютно интегрируемая на функция, то функции a(y) и b(y), определенные равенствами

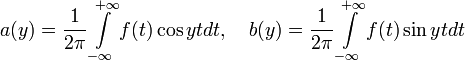
Доказательство. Докажем, например, непрерывность a(y). Из уравнения для a(y) следует, что

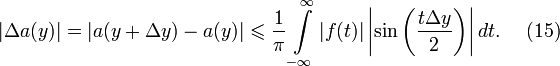
Так как функция f(t) абсолютно интегрируема, то интервал можно разбить на три таких интервала и , что по бесконечным интервалам интегралы от функции | f(x) | не будут превышать . второй итнеграл меньше чем

,

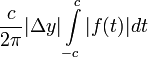и, следовательно, существует δ > 0 такое, что при | Δy | < δ второй интеграл меньше . Следует, что при | Δy | < δ приращение .