
- •1. Определение первообразной и её свойства
- •2. Неопределённый интеграл,таблица основных интегралов
- •3. Инвариантность формул интегрирования
- •4.Непосредственное интегрирование
- •5,Интегрирование методом замены переменной(метод подстановки)
- •6. Метод интегрирования по частям
- •7.Примеры интегрирования рациональных функций
- •8 .Интегрирование рациональных дробей
- •Алгоритм интегрирования рациональной дроби
- •9.Разложение рациональных функций в сумму простейших дробей
- •10.Интегрирование иррациональных функций
- •14. Определенный интеграл
- •15.Методы вычисления определенного интеграла
- •17. Формула Ньютона Лейбница
- •20. Дифференциальные уравнения первого порядка
- •21. Задача Коши.
- •22.Теорема существования и единственности решения задачи Коши.
- •23. Уравнения с разделяющимися переменными
- •Уравнения вида
- •24. Ду с однородными функциями
- •25.Линейные дифференциальные уравнения первого порядка
- •Преобразованное уравнение является линейным относительно и . Решив его, найдем общий интеграл уравнения Далее, подставив , получим общее решение уравнения Бернулли
- •27.Уравнение в полных дифференциалах
- •Уравнение может быть записано в виде
- •28.Ду высших порядков…..
- •31.Свойства решений лоду
- •32. Определитель Вронского
- •33. Структура общего решения лоду
- •36. Метод вариации произвольных постоянных
- •38.Лнду 2-го порядка с постоянными коэффициентами со специальной правой частью.
- •Вычисление длины дуги плоской кривой
31.Свойства решений лоду
ДУ
вида
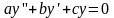 называется линейным
однородным дифференциальным уравнением
с постоянным коэффициентами.Где
a,b,c-постоянные
вещественные числа.
называется линейным
однородным дифференциальным уравнением
с постоянным коэффициентами.Где
a,b,c-постоянные
вещественные числа.
Будем
искать частные решения ДУ в виде
 ,
где
,
где
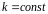 ,
тогда
,
тогда
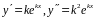 .
.
Подставляя
значения
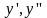 в ДУ, находим
в ДУ, находим
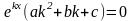
Так
как
 то
получим следующее алгебраическое
выражение
то
получим следующее алгебраическое
выражение
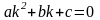
которое называется характеристическим уравнением для ЛОДУ
Совокупность
частных линейно независимых решений
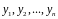 составляет
фундаментальную
систему решений ЛОДУ.
составляет
фундаментальную
систему решений ЛОДУ.
Определение : Компоненты общего решения дифференциального уравнения определяются в зависимости от характера корней характеристического уравнения следующим образом:
1)
каждому действительному простому (т.е.
не кратному) корню
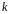 в общем решении соответствует слагаемое
вида
в общем решении соответствует слагаемое
вида
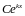 ;
;
2)
каждому действительному корню кратности
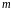 в общем решении соответствует слагаемое
вида
в общем решении соответствует слагаемое
вида
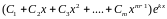 ;
;
3)
каждой паре комплексных сопряженных
простых корней
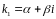 и
и
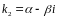 в
общем решении соответствует слагаемое
вида
в
общем решении соответствует слагаемое
вида
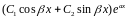 ;
;
каждой паре комплексных сопряженных корней и кратности в общем решении соответствует слагаемое вида
 .
.
32. Определитель Вронского
Определение. Система функций называется линейно независимой на некотором промежутке, если ни одна из этих функций не представляется в виде линейной комбинации всех остальных.
В
случае двух функций
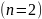 это означает, что
это означает, что
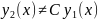 ,
т.е.
,
т.е.
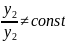 .
Последнее условие можно переписать в
виде
.
Последнее условие можно переписать в
виде
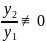 или
или
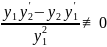 .
Стоящий в числителе этого выражения
определитель
.
Стоящий в числителе этого выражения
определитель
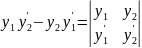 называется определителем Вронского
для функций
и
.
Таким образом, определитель Вронского
для двух линейно независимых функций
не может быть тождественно равен нулю.
называется определителем Вронского
для функций
и
.
Таким образом, определитель Вронского
для двух линейно независимых функций
не может быть тождественно равен нулю.
Пусть
 – определитель Вронского для линейно
независимых решений
и
уравнения (2.3). Убедимся подстановкой,
что функция
– определитель Вронского для линейно
независимых решений
и
уравнения (2.3). Убедимся подстановкой,
что функция
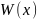 удовлетворяет уравнению
удовлетворяет уравнению
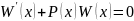 .
(3.1)
.
(3.1)
Действительно,
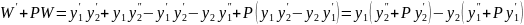 .
Поскольку функции
.
Поскольку функции
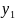 и
и
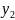 удовлетворяют уравнению (2.3), то
удовлетворяют уравнению (2.3), то
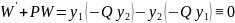 ,
т.е.
,
т.е.
 – решение уравнения (3.1). Найдем это
решение:
– решение уравнения (3.1). Найдем это
решение:
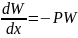 ;
;
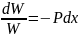 .
Откуда
.
Откуда
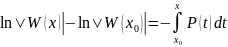 ,
,
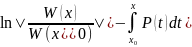 .
.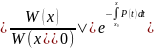 ,
,
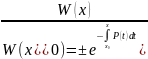 ,
,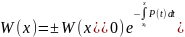 .
.
В
правой части этой формулы надо взять
знак плюс, так как только в этом случае
при
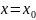 получается тождество. Таким образом,
получается тождество. Таким образом,
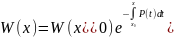 (3.2)
(3.2)
Это
формула называется формулой Лиувилля.
Выше было показано, что определитель
Вронского для линейно независимых
функций не может быть тождественно
равен нулю. Следовательно, существует
такая точка
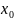 ,
в которой определитель для линейно
независимых решений уравнения (2.3)
,
в которой определитель для линейно
независимых решений уравнения (2.3)
 отличен от нуля. Тогда из формулы
Лиувилля следует, что функция
будет отлична от нуля при всех значениях
отличен от нуля. Тогда из формулы
Лиувилля следует, что функция
будет отлична от нуля при всех значениях
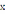 из рассматриваемого промежутка, поскольку
при любом значении
оба множителя в правой части формулы
(3.2) отличны от нуля.
из рассматриваемого промежутка, поскольку
при любом значении
оба множителя в правой части формулы
(3.2) отличны от нуля.
33. Структура общего решения лоду
Теорема.
Если
и
– линейно независимые решения уравнения
(2.3), то их линейная комбинация
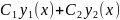 ,
где
,
где
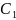 и
и
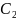 –
произвольные постоянные, будет общим
решением этого уравнения.
–
произвольные постоянные, будет общим
решением этого уравнения.
Доказательство.
То,
что
 есть
решение уравнения (2.3), следует из теоремы
о свойствах решений лоду 2-го порядка.
Надо только еще показать, что решение
будет общим,
т.е. надо показать, что при любых начальных
условиях
есть
решение уравнения (2.3), следует из теоремы
о свойствах решений лоду 2-го порядка.
Надо только еще показать, что решение
будет общим,
т.е. надо показать, что при любых начальных
условиях
 ,
,
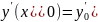 можно выбрать произвольные постоянные
и
так,
чтобы удовлетворить этим условиям.
Запишем начальные условия в виде:
можно выбрать произвольные постоянные
и
так,
чтобы удовлетворить этим условиям.
Запишем начальные условия в виде:

Постоянные
и
из
этой системы линейных алгебраических
уравнений определяются однозначно, так
как определитель этой системы
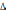 есть значение определителя Вронского
для линейно независимых решений лоду
при
:
есть значение определителя Вронского
для линейно независимых решений лоду
при
:
 ,
,
а такой определитель, как мы видели в предыдущем параграфе, отличен от нуля. Теорема доказана.
34-35Линейные неоднородные уравнения второго порядка с постоянными коэффициентами.
Рассмотрим случай линейного неоднородного дифференциального уравнения с постоянными коэффициентами ЛНДУ
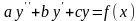 (2),
(2),
где
a,
b,
c
-
действительные постоянные, а
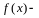 непрерывная на некотором интервале
функция.
непрерывная на некотором интервале
функция.
Теорема 7.2. (о структуре общего решения ЛНДУ):
Общее
решение y
ЛНДУ
(2) есть сумма общего решения y0
соответствующего однородного уравнения
ЛОДУ
и любого частного решения
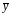 неоднородного уравнения:
неоднородного уравнения:

Таким образом, чтобы найти общее решение ЛНДУ, нужно найти общее решение соответствующего ЛОДУ и какое-нибудь частное решение ЛНДУ. В общем случае задача отыскания частного решения является сложной.
Частное решение ЛНДУ можно найти методом вариации произвольных постоянных или методом подбора (метод неопределенных коэффициентов
по виду правой части уравнении.)
