1.2.5. Стереографическая проекция, её свойства. Сфера Римана, расширение комплексной плоскости

Наряду с плоскостью С рассмотрим расширенную комплексную плоскость 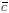, полученную добавлением элемента .

Наглядной моделью расширенной комплексной плоскости является сфера. Рассмотрим стереографическую проекцию сферы на плоскость:

.

ц =(0, 0, ), r = .

Такое отображение – стереографическая проекция – является взаимно - однозначным отображением сферы с выколотым “сферическим полюсом” на комплексную плоскость; она задается формулами: , , .

Прямая:

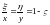
Рассмотрим теперь “идеальное” комплексное число , которое сопоставлено “сферическому полюсу” сферы S и называется бесконечной удаленной точкой (бесконечностью) – расширенная комплексная плоскость, С – конечная комплексная плоскость.

Имеем взаимно - однозначное соответствие между и S и между С и S\{0,0,1}.

Такая интерпретация комплексных чисел предложена Риманом. Это одноточечная компактификация комплексной плоскости.

Интерпретация Римана в определенных случаях позволяет рассматривать как равноправный элемент плоскости .

Однако точка не участвует в алгебраических операциях и не является полем.

Исключения:

1) +а = а+ = , ,

2) а/0 = *а = а* = , где \{0}.

3) а/ = 0, /а = , где .

1.2.6.Некоторые свойства стереографической проекции.

Лемма1. При стереографической проекции всякая окружность в широком смысле(т.е. окружность или прямая) комплексная плоскость С переходит в окружность сферы и наоборот.

■ Уравнение окружности в широком смысле на плоскости имеет вид:

При А = 0 имеем прямую, при А 0 – окружность.

Т.к. при стереографической проекции , то для образов точек окружности получаем соотношение , или , . Т.е. некоторой плоскости в кроме того, , т.е. окружности.

И на оборот точки окружности на S принадлежат и некоторой плоскости, т.е.удовлетворяет некоторому уравнению это окружность на С.

При этом: окружность на S проходит через точку (0,0,1) тогда и только тогда, когда А=0; значит, в этом случае окружность на S переходит в прямую на С. ■

Лемма 2. Величины углов между кривыми при стереографическом отображении сохраняются.

Теорема 6. (1-ая теорема Абеля)

Пусть ряд (4) -сходится в точке . Тогда степенной ряд (4) абсолютно и равномерно сходится в замкнутом круге .

Т.к. ряд - сходится

то в силу необходимого признака сходимости ряд последовательность . Но всякая сходящаяся последовательность ограничена, поэтому .Поскольку ряд - сходится (как геометрическая прогрессия со знаменателем q<1). То ряд (4) сходится в , причем равномерно. Т.к. выбираем произвольно, то ряд (4)сходится и в открытом круге , но быть может не равномерно.

Следствие. Если множество сходимости степенного ряда (4) отлично от {0} и

такое, что ряд (4) сходится в круге , расходится на множестве .На окружности ряд (4) может сходится и расходится.