5.3 Метод замены переменной.

Алгоритм решения:

1. Берем некоторое выражение за новую переменную t.

2. Заменяем dx по формуле: .

3. Подставляем в изначальное выражение.

4. Делаем обратную замену.

Советы:

1. Берите «средние» функции – не простые и не сложные (Пример: (kx+m) – простая функция, - сложная, - средняя).

2. Старайтесь брать за t так, чтобы в итоге все оставшиеся после замены выражения с х сократились с .

3. Ничего страшного если взяли за t не то выражение, возьмите другое.

Примеры:

11.9 .

Решение:

1. t=arctg(x)

2. 

3. .

11.15

Решение:

1. 

2. 

3. .

11.27

Решение:

1. 

2. 

3. .

5.4 Определенный интеграл.

Определенный интеграл высчитывается точно также как и неопределенный, но в конце мы подставляем значения пределов интегрирования по четвертому свойству интегралов.

Пример:

11.54 = .

5.5 Двойные интегралы.

Двойной интеграл имеет вид: , где D – пределы интегрирования по х и по у.

Чтобы решить данный интеграл необходимо взять поочередно определенный интеграл по одной переменной, а затем по другой. При этом стоит учитывать, что если пределы интегрирования заданы константами, то нет разницы, какой интеграл сначала брать: по х или по у, но если один из пределов задан через переменную, то необходимо сначала взять интеграл с переменной в пределах интегрирования.

Примеры:

18.1

Решение:

Запишем в виде:

Т.е. мы взяли сначала интеграл по х с пределами интегрирования по х, а затем по у с пределами интегрирования у.

18.2

Этот пример осложнен тем, что один из пределов интегрирования выражается через переменную. Возьмем сначала интеграл по у (т.к. его предел интегрирования выражается через х), а затем по х:

18.12

Решение:

=

P.S. Заметьте, что когда мы берем интеграл от -6х по у, мы получаем -6ху, т.к. считаем, что в этом случае х – константа (что аналогично взятию производной от функции нескольких переменных)

Глава VI. Точки экстремума функции нескольких переменных.

6.1 Локальный экстремум функции.

Для того чтобы найти точки минимума/максимума функции необходимо выполнить два условия:

1. Необходимое условие. Находим все возможные критические точки.

Для этого необходимо приравнять каждую производную функции по всем переменным к нулю, а затем решить систему.

2. Достаточное условие. Находим точки минимума и максимума.

Теперь необходимо работать с матрицой Гессе:

Во-первых, необходимо найти все вторые производные матрицы и заполнить таблицу.

Во-вторых, если у нас >0 либо <0 в некой критической точке, то перед нами точка минимума, а если знаки чередуются (например, ), то максимума. В ином случае – точки экстремума нет.

.

P.S. соответственно, если у нас функция не от 3х переменных, а от двух, то матрица Гессе будет 2х2 и 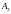не будет вообще.

Пример:

16.1.

1) . Как видно у нас всего одна критическая точка.

2) 8 max.

Ответ: (1;2) – точка максимума.

16.17.

1. 

2. .

Определим сначала точку : - max.

Теперь точку : - не является экстремумом.

Ответ: (-1;-3;-2) – max.

6.2 Локальный условный экстремум.

Отличается локальный условный экстремум, лишь некоторыми нововведениями:

Примеры:

Решение:

1. Выразим х через у и подставим в z:

Теперь найдем критические точки, взяв производную и приравняв ее к 0.

.

2. Можно решать через матрицу Гессе, а можно вспомнить школьный курс:

Отсюда видно, что в точке у=1,5 – максимум.

Ответ: - max.

17.24. Найдите наибольшее и наименьшее значения функции в области, ограниченной осями координат и прямой .

Решение:

Эта задача отличается тем, что мы ищем максимальное и минимальное значение z, а не только точки максимума минимума, это значит, что нужно смотреть чему z равняется на границах.

1. Найдем точки экстремума: и найдем значение z в этой точке:

2. Сделаем чертеж области:

И найдем значения z в указанных точках:

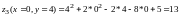
3. Найдем критические точки на прямых, ограничивающих область:

Ось ОХ: на оси х , значит на этой прямой , а значит: .

Ось ОУ: на оси у х=0, значит на этой прямой , а значит:

Прямая : .

4. Выбираем минимальное и максимальное значение z.

Ответ: .