
- •18. Автоматы Мили с конечной памятью. Теорема Гилла.
- •19. Автоматы Мура. Теорема о сокращении. Теорема о неопределенности. Следствия.
- •20. Построение равносильного автомату Мили автомата Мура.
- •21.Построение равносильного автомату Мура автомата Мили.
- •22. Гомоморфизм и изоморфизм автоматов Мура.
- •23. Автоматы с магазинной памятью (мпа). Формальное представление. Принципы функционирования.
- •24. Язык мпа.
- •25 Машина Тьюринга (мт). Формальное представление. Принципы функционирования. Языки мт. Понятие останова мт.
- •26 Модификации мт. Память в состоянии. Многодорожечная мт. Подпрограммы.
- •27. Расширения мт. Многодорожечные мт. Недетерминированные мт.
- •28 Мт с ограничениями. Мт с полубесконечной лентой. Мультистековые мт. Счетчиковые мт.
- •29. Вычислительная мощность мт.
- •31. Регулярные выражения (рв) и языки. Операторы рв. Приоритеты операторов. Связь рв, дка, ε-нка, нка.
- •32. Преобразование дка в рв.
- •33. Преобразование дка в рв. Метод сокращения состояний.
- •34. Преобразование рв в конечный автомат.
- •35. Применение регулярных выражений.
- •37.Свойства регулярных языков (ря). Лемма о накачке для ря.
- •38. Свойства замкнутости ря
- •Временная сложность взаимных преобразований представлений регулярных языков. Вопросы разрешимости ря.
- •41.Деревья разбора. Определения. Свойства. Примеры.
- •42.Связь ксг с конечными автоматами. Нормальная форма Хомского.
- •43. Принцип микропрограммного управления. Теорема Глушкова. Понятия операционного и управляющих автоматов.
- •50.Кодирование внутренних состояний ца.
№ 1. Области применения теории автоматов. Основные определения.
Исследовании абстрактных устройств, поиск границ выч. сис.
1930- Машина Тьюринга.
50-40е- проблемы простейших машин (конечных автоматов).
конец 50х- Хомский, изучение грамматик.
69г- Кук, обобщение работ Тьюринга о границах применения ВМ, определил классы задач(разрешимые, трудноразрешимые).
Прог-ы для работы цифровых схем.
Лексические организаторы компиляторов.
ПО для текстового поиска в больших объёмах, поисковые машины.
ПО для проверки передачи данных. ПО для для сис-м с конечным кол-ом состояний.
Создание последовательных схем, создание криптографических протоколов.
ТА- подходит для описания любых систем имеющее конечное число состояний.
![]()
Конечный автомат- можно определить как дискретный преобразователь инф-ии переходящей из одного состояния в др. по хходным сигналам и имеющий определённое кол-во вых-х состояний.
Грамматики- тип моделей используемых при проектировании программного обеспечения обрабатывающего данные рекурсивной структурой.
Регулярные выражения- задают структуру данных, называемые шаблонами цепочек символов, альтернативный кон. авт-т.
№ 2. Система обозначений теории автоматов. Алфавит, цепочка, степень алфавита, язык, конкатенация цепочек.
Алфавит-
наз-ся конечное не пустое множество
символов(двоичные символы, числа и др.)
обозначается
![]() , то из чего состоит {0,1}
, то из чего состоит {0,1}
![]()
Цепочка
символов(слово)- конечная
последовательность символов некоторого
алфавита, обозначается: если
![]() то
001, 010, 110,…
то
001, 010, 110,…
![]() -
пустая цепочка (е), |w|-
длина цепочки.
-
пустая цепочка (е), |w|-
длина цепочки.
Степень
алфавита- если
есть
,
то алфавитом
![]() называется множество всех цепоче длиной
k
состоящих из символов алфавита.
называется множество всех цепоче длиной
k
состоящих из символов алфавита.
Конкатенация цепочек x и y: xy : к х добавляем цепочку y.
x=a,b,c ; y=c,d,e
xy=a,b,c,d,e;
xy![]()
Язык- мн-во цепочек, каждая из которых принадлежит мн-ву всех цепочек алф-та.
![]() называется
языком над алфавитом
.
называется
языком над алфавитом
.
№3. Детерминированный конечный автомат (ДКА). Формальное представление. Диаграмма переходов, таблица переходов.
Детерминированный конечный автомат- называется кон-й авт-т который прочитав произв-ую последовательность символов может находиться не более чем в одном состоянии.
Компоненты ДКА:
мн-во состояний (Q).
мн-во входных символов ( ).
функция перехода
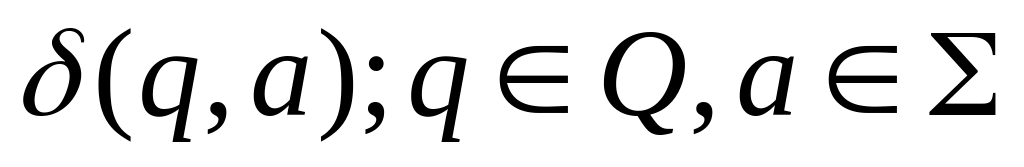 .
.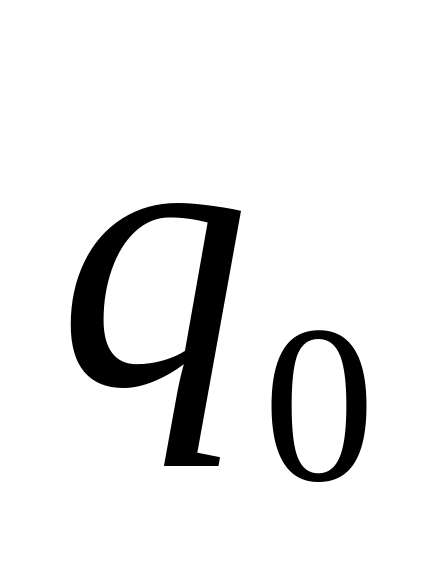 -начальное
состояние
-начальное
состояние
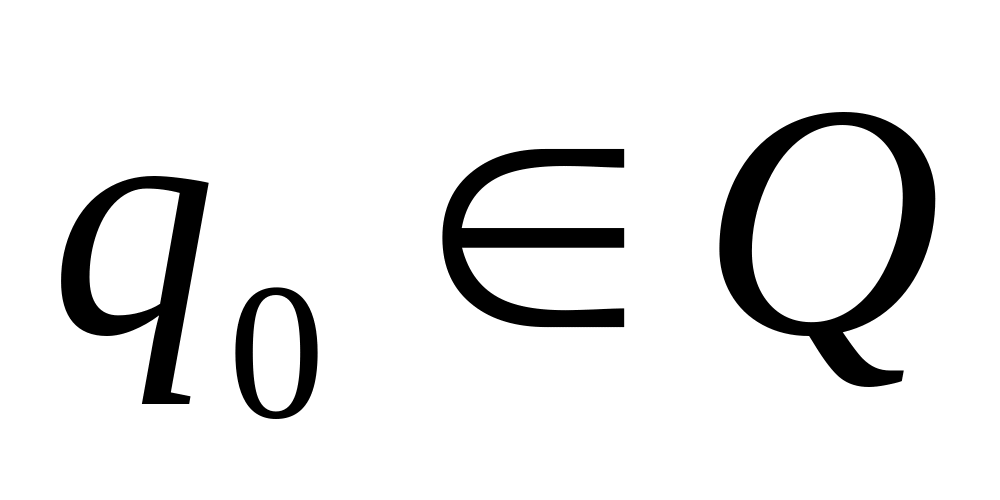 .
.мн-во допускающих состояний F.
Формальное
представление:
![]()
Диаграмма переходов:

Тоблици:
строки- это состояния, столбцы- входные символы.
|
0 |
1 |
|
|
|
|
|
|
|
|
|
№4. Функция переходов ДКА. Расширенная функция переходов ДКА. Язык ДКА.
Расширенная функция переходов ДКА
![]() ,
где
,
где
![]()
![]()
Язык
ДКА:
![]() Если L
некий язык ДКА, то L
является регулярным языком.
Если L
некий язык ДКА, то L
является регулярным языком.
№5. Недетерминированный конечный автомат (НКА). Формальное представление. Язык НКА.
НКА- находится в нескольких состояниях одновременно. Такую возможность автомата можно расценивать как «предсказание» входящего сигнала.
НКА:
-допускают регулярные языки.
-имеют те же компоненты что и ДКА.
-строятся легче ДКА и получаются проще.
-НКА можно перевести в эквивалентный ДКА
Компоненты НКА:
-множество состояний
-множество входных символов
-функция переходов
-начальное состояние, мн-во допускающих состояний
-существенное
отличие в функ-ях перехода
![]()
Формальное представление:
![]()
|
0 |
1 |
q0 |
q1 |
q1q0 |
q1 |
|
q2 |
q2 |
|
|
Язык НКА: есть некоторый автомат , то языком данного автомата будет мн-во цепочек расширенной функции переходов для которых пересекается с мн-ом допускающих состояний автоматов.
Расширенная
функция переходов НКА:
![]() -даная
функция есть мн-во состояний в которые
попадает автомат при чтении цепочки w.
-даная
функция есть мн-во состояний в которые
попадает автомат при чтении цепочки w.
№6.Эквивалентность ДКА и НКА. Конструкция подмножеств.
Эквивалентность ДКА и НКА:
Любой язык который допускается НКА допускается и ДКА, при этом ДКА может иметь больше состояний или столько же и иметь больше переходов чем НКА. В худшем случае для НКА с n состояниями эквивалентный ему ДКА будет содержать 2n состояний.
Конструкция
подмножеств.
Пусть есть два автомата НКА и ДКА
![]() ,
,
![]() ,
,![]()
![]() -
есть мн-во всех подмн-в мно-ва
-
есть мн-во всех подмн-в мно-ва
![]() -
булеан, если число состояний
-
булеан, если число состояний
![]() ,
то
,
то
![]() .
.
Мн-во
![]() -есть
мн-во подм-в
-есть
мн-во подм-в
![]() для которых выполняется
для которых выполняется
![]() .
.
- есть всё мн-во состояний автомата N которые содержат хотябы одно допускающее состояние.
Для
любого подмн-ва S
из
для любого символа входного алфавита
![]()
№7. Преобразование ДКА в НКА
Пусть N— автомат на рис допускающий цепочки, которые оканчиваются на 01. Поскольку множество состояний N есть {qo, q1, q2}, то конструкция подмножеств дает ДКА с 23 = 8 состояниями, отвечающими всем подмножествам, составленным из этих трех состояний. На рис. 2.12 приведена таблица переходов для полученных восьми состояний. Объясним вкратце, как были получены элементы этой таблицы.
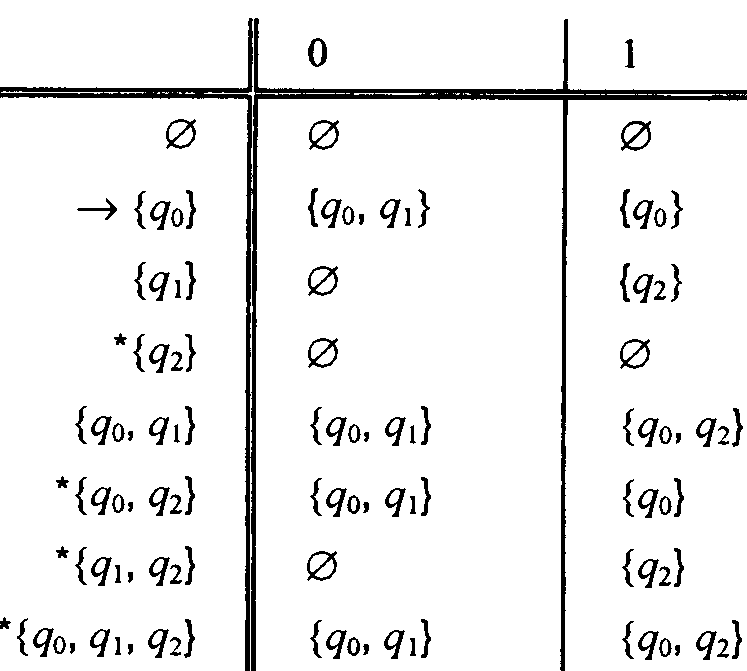
Заметим,
что данная таблица, элементами которой
являются множества, соответствует
детерминированному конечному автомату,
поскольку состояния построенного ДКА
сами
являются множествами. Для
ясности можно переобозначить состояния.
Например,
![]() обозначить
как A,
{q0}
—
как В
и
т.д. Таблица переходов для ДКА на рис.
2.13 определяет в точности тот же автомат,
что и на рис. 2.12, и из ее вида понятно,
что элементами таблицы являются
одиночные состояния ДКА.
обозначить
как A,
{q0}
—
как В
и
т.д. Таблица переходов для ДКА на рис.
2.13 определяет в точности тот же автомат,
что и на рис. 2.12, и из ее вида понятно,
что элементами таблицы являются
одиночные состояния ДКА.

Начиная в состоянии В, из всех восьми состояний мы можем попасть только в состояния В, Е и F. Остальные пять состояний из начального недостижимы, и поэтому их можно исключить из таблицы. Часто можно избежать построения элементов таблицы переходов для всех подмножеств, что требует экспоненциального времени. Для этого выполняется следующее "ленивое вычисление" подмножеств.
№10. Конечные автоматы с эпсилон переходами (ε-НКА). Формальное представление. Ε-замыкание.
Конечные автоматы с эпсилон переходами (ε-НКА).
ξ-НКА является расширенным НКА.
Рассмотрим:
Σ={+,-, ., 0,…,9}
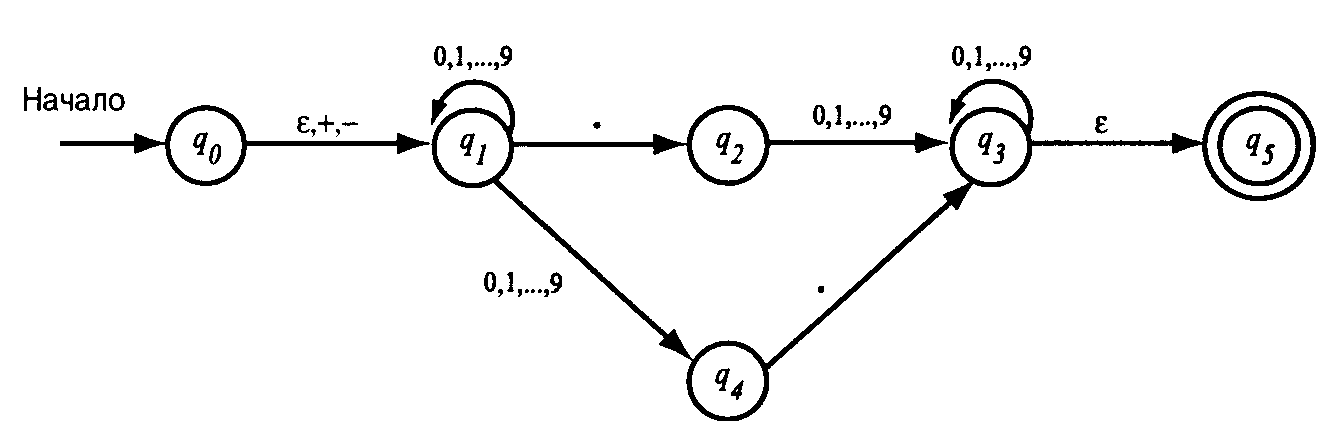
![]()
Ε-замыкание.
Говоря нестрого, мы получаем е-замыкание состояния q, совершая все возможные переходы из этого состояния, отмеченные е. Но после совершения этих переходов и получения новых состояний снова выполняются е-переходы, уже из новых состояний, и т.д. В конце концов, мы находим все состояния, в которые можно попасть из q по любому пути, каждый переход в котором отмечен символом е. Формально мы определяем е-замыкание, ECLOSE, рекурсивно следующим образом.
Базис. ECLOSE(g) содержит состояние q.
Индукция. Если ECLOSE^) содержит состояние р, и существует переход, отмеченный е, из состоянияр в состояние г, то ECLOSE(<7) содержит г. Точнее, если 8 есть функция переходов рассматриваемого е-НКА и ECLOSE(g) содержит р, то ECLOSE(g) содержит также все состояния из 8{р, е).
Формальная запись е-НКА
е-НКА
можно представлять точно так же, как и
НКА, с той лишь разницей, что функция
переходов должна содержать информацию
о переходах по е. Формально, е-НКА А можно
представить в виде А = (Q, Е, δ, q0, F), где
все компоненты имеют тот же смысл, что
и для НКА, за исключением д, аргументами
которой теперь являются состояние из
Q и элемент множества ∑
![]() {ε},
т.е. либо некоторый входной символ, либо
е.
{ε},
т.е. либо некоторый входной символ, либо
е.
№11. Язык ε-НКА. Связь языков ε-НКА и ДКА.
Язык ε-НКА: есть мн-во цепочек состоящих из символов алфавита для которых расширенная функция перехода даёт хоть 1 допускающее состояние.
Связь языков ε-НКА и ДКА: Для любого ε-НКА можно найти ДКА допускающий тот же язык.
![]()
![]()
1.
-мн-во
подмножеств
![]() (только
замк.)
(только
замк.)
![]()
2.
![]() =ECLOSE(
=ECLOSE(![]() )
)
3.
![]()
4.
![]()
a.
S={S,…,![]() }
}
б.
вычислим
![]()
в.
![]()
№12. Преобразование ε-НКА в ДКА.
Для всякого ξ-НКА Е можно найти ДКА D, допускающий тот же язык, что и Е. Поскольку состояния D являются подмножествами из состояний Е, то используемая конструкция очень напоминает конструкцию подмножеств. Единственное отличие состоит в том, что нужно присоединить еще и ξ -переходы Е, применив механизм ξ -замыкания.
Пусть Е = (QE, Σ, δе, qE, FЕ). Тогда эквивалентный ДКА
D = (Qd,Σ, δD, qD, FD) определяется следующим образом.
1.
QD
есть
множество подмножеств QE
Точнее,
как мы выясним, для D
допустимыми
состояниями являются только ξ
-замкнутые подмножества QE,
т.е.
такие множества S![]() QE,
для
которых S
= ECLOSE(S).
Иначе говоря, ξ -замкнутые множества
состояний S—
это такие множества, у которых всякий
ξ -переход из состояния, принадлежащего
S,
приводит
снова в состояние из S.
Заметим,
что
QE,
для
которых S
= ECLOSE(S).
Иначе говоря, ξ -замкнутые множества
состояний S—
это такие множества, у которых всякий
ξ -переход из состояния, принадлежащего
S,
приводит
снова в состояние из S.
Заметим,
что
![]() есть ξ -зам-кнутое множество.
есть ξ -зам-кнутое множество.
2. qD — ECLOSE(g0), т.е., замыкая множество, содержащее только начальное состояние Е, мы получаем начальное состояние D. Заметим, что это правило отличается от использованного ранее в конструкции подмножеств — там за начальное состояние построенного автомата принималось множество, содержащее только начальное состояние данного НКА.
3.
FD
—
это такие множества состояний, которые
содержат хотя бы одно допускающее
состояние автомата Е.
Таким
образом, FD
= {S
| S
принадлежит
QD
и
S
![]() FE
FE
![]() }.
}.
4. S0(S, а) для всех а из Σ и множеств S из QD вычисляется следующим образом:
а) пусть S= {p1 ,p2 ,…,pk }
б)
вычислим
![]() ;
пусть
это будет множество {r1
,r2
,…,rm)
;
пусть
это будет множество {r1
,r2
,…,rm)
в)
тогда
![]()
№13. Автоматы Мили. Эквивалентные автоматы Мили. Сокращенные автоматы Мили.
![]()
![]()
![]()
Отличительной особенностью АМ является то, что их выходные символы зависят как от состояния автомата так и от входных символов. Может задаваться как в виде графа, так и виде таблицы.
Эквивалентные автоматы Мили.
Состояние
q
и
![]() из мн-ва Q
называются эквивалентными (q
=
)
в том случае если
из мн-ва Q
называются эквивалентными (q
=
)
в том случае если
![]()
Автоматы
M
и
![]() называются эквивалентными если они
имеют одинаковые реакции.
называются эквивалентными если они
имеют одинаковые реакции.
Реакцией
состояний q
наз-ся порождённые этим состоянием вх
и вых отображения. Это результат функции
![]() и
и
![]() на вх символ, на мн-во реакций его
состояний
на вх символ, на мн-во реакций его
состояний
![]() Сокращенные
автоматы Мили.
Сокращенные
автоматы Мили.
Автомат М наз-ся сокращённым если любые два состояния этого автомата не являются эквивалентными.
№14. Прямое произведение автоматов Мили. Теорема Мура.
Прямым произведением автоматов А и В с одинаковыми алфавитами называется автомат:
![]() где
где
![]() ,
,
![]()
![]()
![]()
![]()
Теорема Мура:
Два
конечных автомата А и В с одинаковым вх
алфавитом являются эквивалентными
тогда и только тогда когда для любого
достижимого состояния
![]() ,
,![]() в их прямом произведении справедливо:
в их прямом произведении справедливо:
![]()
№15. Теорема Хаффмана-Мили. Следствия.
Теорема Хаффмана-Мили:
Для эквивалентности двух состояний автомата Мили имеющего n состояний достаточно чтобы совпадали реакции этих состояний на на входные последовательности не превышающие n-1.
Следствия:
проблемой эквивалентности состояний автомата Мили является РАЗРЕШИМОЙ .
М и с количеством состояний m и n соответственно на все входящие последовательности длинны меньше чем m+n-1 СОВПАДАЮТ.
№16. Теорема о сокращении. Различимость входных последовательностей.
Теорема о сокращении:
Для любого автомата Мили может быть эффективно построен сокращённый автомат Мили.
Док-во.
Эквив-ый
автомат Мили получается при объединении
всех эквив-х состояний в одно общее
состояние при определении соответствующих
образующих функций. Положим что группа
состояний
![]()
![]()
где
![]()
![]()
Легко
увидеть что функции
![]() и
и
![]() корректны и автоматы
корректны и автоматы
![]() действительно эквиваленты.
действительно эквиваленты.
Различимость входных последовательностей.
Две входные последовательности v и w из F(X) называются неразличимыми автоматом А, если для любого z из Z и любого и из F(X) выполняется равенство g*(z, vu)=g*(z, wu). В противном случае последовательности v и w называются различимыми автоматом А. Автомат А называется различающим входы, если любые две входные последовательности различимы автоматом А.
№17.Теорема Чена. Реакция автомата Мили на периодические последовательности. Теорема о периодичности.
Теорема Чена
Пусть
М является автоматом Мили с n
состояниями, если любые две последовательности
длинны
![]() являются различимыми автоматом М, то
он является автоматом различающим ходы.
являются различимыми автоматом М, то
он является автоматом различающим ходы.
Пусть к — натуральное число.
1) Для каждой цепочки из алфавита Y определим к-окончания (или
k-суффикс) Γк(u) таким образом что:
а) если |u|<k, то Гк(u)=u;
б)
если
![]() ,
n>k
то Γк(u) =
,
n>k
то Γк(u) =![]() ... yn.
... yn.
2) Две входные последовательности v и w называются k-финально неразличимыми автоматом М, если для всех состояний и всех цепочек из алфавита выполняется равенство
гk(![]() (q,
vu))=гk(
(, wu)).
В противном случае v и w называются
k-финально различимыми автоматом М.
(q,
vu))=гk(
(, wu)).
В противном случае v и w называются
k-финально различимыми автоматом М.
Реакция автомата Мили на периодические последовательности:
Теорема о периодичности:
Пусть q произвольное состояние автомата М и n- число состояний которых можно достичь из состояния q.
Пусть
подаётся последовательность
![]() .
Существуют числа r
и p
для которых для любого m>=r
символ с индексом
.
Существуют числа r
и p
для которых для любого m>=r
символ с индексом
![]() .
.
Пусть
подаётся цепочка
![]() тогда существуют натуральные числа
такие что:
тогда существуют натуральные числа
такие что:
1.
![]()
2.
существует число
![]()
3.
![]()
Для
любого i>=s
и любого числа k<=j-s+1
последние к-входов автомата М получившего
на вход цепочки
![]() и
и
![]() являются равными.
являются равными.
![]()
18. Автоматы Мили с конечной памятью. Теорема Гилла.
Автомат Мили A=(Z, X, Y, f, g) называется автоматом Мили с конечной памятью, если для него существуют натуральные числа р, q и отображение h:Xp+1+YqY такие, что для всех z из Z и всех слов w=xi... xk из F(X), где k> max(p, q), выполнено равенство yk=h(Xk, Xk-i,..., Xk-p, Ук-l, Ук-2, -..,Ук-q)
[при этом считается, что yi … yk=g*(z, Xi...Xk)].
Наименьшее число m, для которого существуют не превышающие его числа р и q [т. е. m=max(p, q)], удовлетворяющие, веденному выше условию, называется памятью автомата Мили А.
Итак, автомат Мили имеет конечную память m, если существует функция h, с помощью которой выход автомата в любой наперед заданный момент времени k может быть определен только по входу Xk в этот момент и по входам и выходам Xk-1,...,Xk-m и Yк-1,...,Yк-m в предыдущие m моментов времени, без учета состояний самого автомата.
Теорема Гилла:
Существует конечный автомат Мили, не обладающий конечной памятью
Пусть существует автомат Мили с конечной памятью m и n состояниями, тогда m=<n(n-1)/2
![]()
19. Автоматы Мура. Теорема о сокращении. Теорема о неопределенности. Следствия.
Автомат Мура есть пятерка A=(Z, X, Y, f, h). Здесь h - сюръективное отображение из Z в Y, называемое функцией выходов. Ясно, что автоматы Мура (как и автоматы Мили) могут быть описаны не только ориентированными графами, но и таблицей для функций f и h или матрицей переходов и таблицей для h.
Пусть А - автомат Мура. Положим g(z, x)=h(f(z, x)) для каждого z из Z и каждого х из X. Тогда B=(Z, X, Y, f, g) — автомат Мили, который для всех непустых входных последовательностей порождает такие же выходные последовательности, как и автомат А, если, конечно, не учитывать самый первый выход автомата А.
Пусть А - автомат Мура в обычных обозначениях и f*: ZxF(X)Z
Реакцией hz состояния z называется отображение hz: F(X)F(Y), задаваемое следующим образом:
hz(Λ)=h(z);
hz(x)=h(Λ)h(f(z, x))=h(z)h(f(z, х)) - для всех х из X;
hz(wx)=hz(w)h(f(f*(z, w),x))=hz(w)h(f*(z, wx)) - для всех w≠Λ из F(X) и всех х из X.
Теорема о сокращении. Два состояния автомата Мура с n состояниями и m выходами эквивалентны, если их реакции на все входные последовательности длины, не большей n-m, одинаковы. Таким образом, для каждого автомата Мура может быть эффективным образом построен эквивалентный сокращенный автомат Мура.
Теорема о неопределенности. Существует сокращенный автомат Мура A(Z, X, Y, f, h) такой, что ни для одного слова w из F(X) не выполнено условие:
hz(w)≠hz'(w) для всех z и z' из Z таких, что z≠z'.
Следствия:
1) Класс автоматов Мили, представимых как автоматы Мура, не замкнут относительно операции сокращения.
2) Сокращенный автомат Мура, представленный как автомат Мили, не обязательно является сокращенным.
