4. Математическая модель «хищники-жертвы»

Впервые в биологии математическую модель периодического изменения числа антагонистических видов животных предложил итальянский математик В. Вольтерра с сотрудниками. Модель, предложенная Вольтерра, явилась развитием идеи, намеченной в 1924 году А. Лоттки в книге «Элементы физической биологии». Поэтому эта классическая математическая модель известна как модель «Лоттки-Вольтерра».

Хотя в природе отношения антагонистических видов более сложные, чем в модели, тем не менее они являются хорошей учебной моделью, на которой можно изучать основные идеи математического моделирования.

Итак, задача: в некотором экологически замкнутом районе живут два вида животных (например, рыси и зайцы). Зайцы (жертвы) питаются растительной пищей, имеющейся всегда в достаточном количестве (в рамках данной модели не учитывается ограниченность ресурсов растительной пищи). Рыси (хищники) могут питаться только зайцами. Необходимо определить, как будет меняться численность жертв и хищников с течением времени в такой экологической системе. Если популяция жертв увеличивается, вероятность встреч хищников с жертвами возрастает, и, соответственно, после некоторой временной задержки, растет популяция хищников. Эта достаточно простая модель вполне адекватно описывает взаимодействие между реальными популяциями хищников и жертв в природе.

Теперь приступим к составлению дифференциальных уравнений. Обозначим число жертв через N, а число хищников через M. Числа N и M являются функциями времени t. В нашей модели учтем следующие факторы:

а) естественное размножение жертв;

б) естественная гибель жертв;

в) уничтожение жертв за счет поедания их хищниками;

г) естественное вымирание хищников;

д) увеличение числа хищников за счет размножения при наличии пищи.

Так как речь идет о математической модели, то задачей является получение уравнений, в которые входили бы все намеченные факторы и которые описывали бы динамику, то есть изменение числа хищников и жертв со временем.

Пусть за некоторое время t количество жертв и хищников изменится на ∆N и ∆M. Изменение числа жертв ∆N за время ∆t определяется, во-первых, увеличением в результате естественного размножения (которое пропорционально имеющемуся количеству жертв):

N₁ = A∙N∙∆t, (1)

где А – коэффициент пропорциональности, характеризующий скорость размножения жертв в данных условиях.

Во-вторых, имеет место уменьшение числа жертв из-за естественного вымирания, тоже пропорциональное их числу в данный момент:

N₂ = - B∙N∙∆t, (2)

где В – коэффициент пропорциональности, характеризующий скорость естественного вымирания жертв.

В основе вывода уравнения, описывающего уменьшение числа жертв из-за поедания их хищниками, лежит идея о том, что чем чаще происходит их встреча, тем быстрее уменьшается число жертв. Ясно также, что частота встреч хищников с жертвой пропорционально и числу жертв и числу хищников, то есть их произведению. Поэтому можно записать:

N₃ = - C∙N∙M∙∆t, (3)

где С – коэффициент пропорциональности, характеризующий частоту встреч жертвы с хищником.

В итоге, с учетом всех трех факторов для изменения числа жертв, можно записать следующее уравнение:

N = A∙N∙∆t - B∙N∙∆t - C∙M∙N∙∆t (4)

Поделив левую и правую часть уравнения (4) на ∆t и перейдя к пределу при ∆t→0, получим дифференциальное уравнение первого порядка:

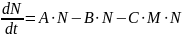(5)

Для того, чтобы решить это уравнение, нужно знать, как меняется число хищников (М) со временем. Изменение числа хищников (∆М) определяется увеличением из-за естественного размножения при наличии достаточного количества пищи (М₁ = Q∙N∙M∙∆t) и уменьшением из-за естественного вымирания хищников (M₂ = - P∙M∙∆t):

M = Q∙N∙M∙∆t - P∙M∙∆t (6)

Из уравнения (6) можно получить дифференциальное уравнение:

(7)

Дифференциальные уравнения (5) и (7) представляют собой математическую модель «хищники-жертвы». Достаточно определить значения коэффициентов A, B, C, Q, P и математическую модель можно использовать для решения поставленной задачи.

Проверка и корректировка математической модели. В данной лабораторной работе предлагается кроме просчета наиболее полной математической модели (уравнения 5 и 7), исследовать более простые, в которых что-либо не учитывается.

Рассмотрев пять уровней сложности математической модели, можно «почувствовать» этап проверки и корректировки модели.

• 1-ый уровень – в модели учтено для «жертв» только их естественное

размножение, «хищники» отсутствуют;

• 2-ой уровень – в модели учтено для «жертв» их естественное

вымирание, «хищники» отсутствуют;

• 3-ий уровень – в модели учтены для «жертв» их естественное

размножение и вымирание, «хищники» отсутствуют;

• 4-ый уровень – в модели учтены для «жертв» их естественное

размножение и вымирание, а также поедание

«хищниками», но число «хищников» остается

неизменным;

• 5-ый уровень – в модели учтены все обсуждаемые факторы.

Итак, имеем следующую систему дифференциальных уравнений:

,

где М – число «хищников»;

N – число «жертв»;

t – текущее время;

A – скорость размножения «жертв»;

C – частота встреч «хищники»-«жертвы»;

B – скорость вымирания «жертв»;

Q – размножение «хищников»;

P – вымирание «хищников».

1-ый уровень: М = 0, В = 0;

2-ой уровень: М = 0, А = 0;

3-ий уровень: М = 0;

4-ый уровень: Q = 0, Р = 0;

5-ый уровень: полная система уравнений.

Подставляя значения коэффициентов в каждый уровень, будем

получать разные решения, например:

Для 3-его уровня значение коэффициента М =0, тогда

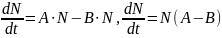
Р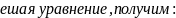

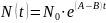
Аналогично для 1-го и 2-го уровней. Что касается 4-го и 5-го уровней, то здесь необходимо решать систему уравнений методом Рунге-Кутта. В результате получим решение математических моделей данных уровней.