
- •1) Евкл пр-во. Откр и замкнутые мн-ва в r2.
- •2) Понятие непрер кривой и области в r2
- •3) Предел послед точек в r2.
- •4) Определение ф-и от неск пер. График ф-и 2х пер.
- •5) Предел ф-и неск пер. Осн теоремы о пределах.
- •6) Непрер ф-и неск пер. Точки разрыва.
- •7) Непрер. Сложной ф-и.
- •8) Основные св-ва непрерывных ф-й
- •9) Равномерная непрер-ть функций 2х переменных
- •10) Частные производные ф-й нескольких переменных
- •11) Дифференцируемость функций нескольких переменных. Понятие дифференциала.
- •12) Необходимые условия дифференцируемости функции двух переменных
- •13) Достаточные условия дифференцируемости функции двух переменных
- •14) Дифференцируемость сложных функций нескольких переменных
- •15) Инвариантность формы дифференциала первого порядка.
- •16) Частные производные высших порядков.
- •17) Дифференциалы высших порядков.
- •18) Формула Тейлора.
- •19) Неявные функции. Дифференцируемость неявных функций.
- •20) Экстремумы функций двух переменных. Необходимое условие экстремума.
- •22) Достаточные условия экстремума для функции 2 переменных.
- •23) Наиб. И наим значение ф-ции 2-х перем. В замкнутой и огр. Обл.
- •26) Определение двойного интеграла. Условия существования двойного интеграла.
- •27) Основные свойства двойного интеграла
- •28)Понятие повторного интеграла для X-правильных областей.
- •29) Понятие повторного интеграла для y-правильных областей.
- •30) Способы вычисления двойного интеграла.
- •31) Замена переменной в двойном интеграле.
- •32) Двойной интеграл в полярных координат
- •36) Определение криволинейного интеграла по координатам (второго рода)
- •37) Свойства криволинейного интеграла второго рода.
- •38) Вычисление криволинейного интеграла второго рода
- •3 9) Криволинейный интеграл второго рода. Формула Грина.
- •40) Условия независимости криволинейного интеграла от путей интегрирования.
- •41) Условия полного дифференциала. Восстановление функции по ее полному дифференциалу.
- •42) Восстановление функции по ее полному дифференциалу
- •44) Криволинейные интегралы по длине дуги(первого рода).
30) Способы вычисления двойного интеграла.
Общая идея вычисления двойного интеграла состоит в сведении двойного интеграла к повторному, однократному, т.е. вычислению двух опред. интегралов.
Введем понятия обл типа 1 (У правильная) и обл типа 2 (Х правильная)
1) Область G на XOY назыв областью типа 1 если любая прямая, парал. оси OY проходящ через внутр точку обл G пересек границу этой обл не более чем в 2х точках.
Ее
записывают так
 (при вычислении X=const)
(при вычислении X=const)
2) обл G назыв обл типа 2 если любая прямая парал оси OX и проходящ через внутр точку обл G пересек границу этой обл не более чем в 2х точках.
Ее
записывают так
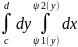
Если D-обл типа 1 и f(x,y) непрерыв в D то =
Если
обл D
- обл типа 2 и f(x,y)
непрерыв в D
то
=
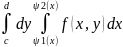
замеч. Если обл D не явл ни обл типа 1 ни обл типа 2 то сначала ее разбив на части так, чтобы каждая ее часть были либо обл типа 1 либо 2,а затем вычисляют
31) Замена переменной в двойном интеграле.
Пусть
в некоторой ограниченной замкнутой
квадрируемой области скости OXY
непрерывная функция f(x,y)
тогда существует двойной интеграл
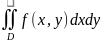 (1)
(1)
функциональный
определитель вида
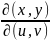 =
=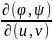 =
= называется якобианом
называется якобианом
Т.
Пусть система функций (2) отображает взаимное однозначно
область D`
на D,
причем функции
(2) отображает взаимное однозначно
область D`
на D,
причем функции
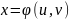 и
и
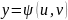 в области D`
имеют непрерывные частные производные
и отличный от нуля якобиан. Тогда, если
существует двойной интеграл (1) то
справедлива формула
=
в области D`
имеют непрерывные частные производные
и отличный от нуля якобиан. Тогда, если
существует двойной интеграл (1) то
справедлива формула
=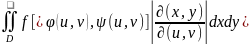 (3)
(3)
Формула (3) называется формулой замены переменных под знаком двойного интеграла
32) Двойной интеграл в полярных координат
Часто вычисление двойного интеграла упрощается заменой декартовых координат х и у полярными координатами ρ и ϕ по следующим формулам:
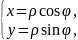 0
≤ ϕ
≤ 2π.
0
≤ ϕ
≤ 2π.
Для
того чтобы получить формулу преобразования
двойного интеграла
с помощью полярных координат, найдём
якобиан функций х
и
у
из
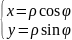 :
:
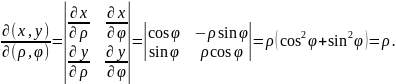
Следовательно,
согласно формуле замены переменных под
знаком двойного интеграла
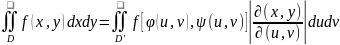 , получаем формулу преобразования
двойного интеграла с помощью полярных
координат:
, получаем формулу преобразования
двойного интеграла с помощью полярных
координат:
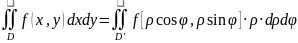 .
.
36) Определение криволинейного интеграла по координатам (второго рода)
Пусть в пространстве OXY дана кусочно-гладкая кривая L=AB, на которой определена ф-ия P(x, y). Разобьём кривую L на n частичных дуг с помощью произвольно выбранных на ней точек
A=M0(x0 , y0), M1(x1 , y1),…, Mk(xk , yk) = B,
Располагающихся
в направлении от А к В. Выберем на каждой
частичной дуге Мk-1Mk
произвольную точку Nk(ξk
, ηk)
и составим суммы σ1= и σ2=
и σ2=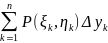 , где ∆xk=xk-xk-1
, ∆yk=yk-yk-1.
(Суммы σ1
и
σ2
называются интегральными суммами, сост
для ф-ии P(x, y) вдоль кривой L=AB
по координате х и у соответсвенно.) Пусть
∆lk
– длина дуги Мk-1Mk
(k=1,2,…,
n),
а λ – наибольшая из ∆lk
(k=1,2,…,
n).
Число J
называется пределом интегральной суммы
σ1
(σ2
) при λ→0,
если для любого ε<0
найдётся δ<0
такое, что как только λ<0,
то выполняется неравенство
|J-
σ1|<ε
(|J-
σ2|<ε)
независимо ни от способа разбиения
кривой L=AB
на части, ни от выбора точек Nk(ξk
, ηk)
на частичных дугах Мk-1Mk
(k=1,2,…,
n).
ИТАК, Если
сущ-ет конечный предел J
интегральной суммы σ1
(σ2
)
при
λ→0,
то он называется криволинейным интегралом
от ф-ии P(x, y) вдоль кривой L=AB
по координате х(у) и обозначается так:
, где ∆xk=xk-xk-1
, ∆yk=yk-yk-1.
(Суммы σ1
и
σ2
называются интегральными суммами, сост
для ф-ии P(x, y) вдоль кривой L=AB
по координате х и у соответсвенно.) Пусть
∆lk
– длина дуги Мk-1Mk
(k=1,2,…,
n),
а λ – наибольшая из ∆lk
(k=1,2,…,
n).
Число J
называется пределом интегральной суммы
σ1
(σ2
) при λ→0,
если для любого ε<0
найдётся δ<0
такое, что как только λ<0,
то выполняется неравенство
|J-
σ1|<ε
(|J-
σ2|<ε)
независимо ни от способа разбиения
кривой L=AB
на части, ни от выбора точек Nk(ξk
, ηk)
на частичных дугах Мk-1Mk
(k=1,2,…,
n).
ИТАК, Если
сущ-ет конечный предел J
интегральной суммы σ1
(σ2
)
при
λ→0,
то он называется криволинейным интегралом
от ф-ии P(x, y) вдоль кривой L=AB
по координате х(у) и обозначается так:
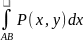 (
(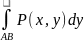 ).
При
этом функция P(x, y) называется интегрируемой
вдоль кривой L=AB
по координате х(у).
).
При
этом функция P(x, y) называется интегрируемой
вдоль кривой L=AB
по координате х(у).
