21)Характ.Многочл.Матр.,собств.В.И собств.Знач.

Ненул.вект. 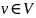назыв.собств.вект.лин.опер. ф:v→V,если сущ.такое

число λ, что ф(v)=λv. Число λ назыв.собств.знач.лин.опер. ф,соотв-ющим

вектору v. Пусть А-матр.лин.опер. ф=V→V в каком либо базисе,тогда

уравнение det(A- λE)=0 назыв.характеристическим; оно не зависит от

выбора базиса,т.е.если взять др.матр.оператора ф в др.базисе,то харак.

уравнен.не изменится.

22)Th:о связи характ.Многочл.И собств.Знач.

Пусть А матрица лин.опер. φ:V→V. Тогда все собств.знач.-есть решения

характеристич. уравнения | A − λE |=0.

| A − λE |= -λ3+(а11+а22+а33)λ2-(А11+А22+А33)λ+detА.

23)Лин.Модель.Обмена

Лин.модель обмена-модель междунар.торговли. Пусть имеется n стран 

S1,S2 ,...,Sn, нац.доход каждой из к-рых = соответственно x1,x2 ,...,xn.

 Обозначим коэффициентами aij долю нац.дохода, которую страна Sj 

тратит на покупку товаров у страны Si. Будем считать, что весь нац.доход

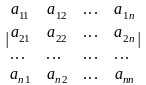
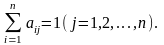тратится на закупку товаров либо внутри страны, либо на импорт из др.

стран, т.е. Рассмотрим матр.А =

которая называется структурной матрицей торговли.

Для любой страны Si (i = 1,2,...,n) выручка от внутр.и

внешн.торговли составит:pi = ai1 x1 + ai2 x2 + ... + ain xn. Для сбалансир.

торговли необходима бездефицитность торговли каждой страны Si, т.е.

выручка от торговли каждой страны должна быть не меньше ее нац.

дохода:pi > = xi (i = 1,2,...,n).

24) Определение и примеры скалярн.Произв.

Скалярным произвед.(a,b) двух векторов a и b называется число, равное

произведен.длин этих векторов на косинус угла φ между ними: (a,b)=ab=

=|a|*|b|*cosφ. Скалярное произведение двух векторов равно сумме

произведений соответствующих координат этих векторв:

(a,b)=ab=|a|*|b|*cosφ= x1x2+y1y2+z1z2.

25)Св-ва скалярн.Произв.

1.(x,y)=(y,x) – коммутативное свойство. 2.(x,y+z)=(y,x)+(x,z) – дистрибутивное

свойство по сложению. 3.((αx),y)=(x,(yα)=α(x,y) – ассоц-ти.относит.умнож.на

скаляр (для любого действительного числа).4.(x,x)≥0, если x-ненулевой вект.,

то строго больше, а если x-нулевой вект.,то =0.

26)Ортонормир.Сист.Вект. Процесс ортогонализации

Для любых элементов этой системы φi,φj скалярное произведение (φi,φj)=δij,

где δij — символ Кронекера.

Ортонормированная система в случае её полноты может быть использована в

к ачестве базиса пространства. При этом разложение любого элемента  

может быть вычислено по формулам:  , где  .

Ортогонализация ― алгоритм построения для данной линейно независ. сист.

векторов евклидова или эрмитова пространства V ортогональной системы 

ненулевых векторов, порождающих то же самое подпространство в V.

Наиболее известным является процесс Грама ― Шмидта, при котором по лин.

независимой системе   строится ортогональная система 

 такая, что каждый вектор bi линейно выражается через

  , то есть матрица перехода от {ai} к {bi} ― верхнетреугольная

матрица.

27)Квадр.Форма.,матр.Кв.Формы,канон.В.

Квадратичной формой L(x1,x2,…,xn) от n переменных назыв. сумма, каждый

член которой является либо квадратом одной из переменных, либо

п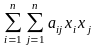 роизведением двух разных переменных, взятых с некоторым коэфф-ом:

L(x1,x2,…,xn)=. Полагаем, что коэффициенты квадратичной

формы аij-действительные числа, причём aij=aji. Матрица А=(аij)(I,j=1,2,…,n),

составленная из этих коэффициентов, называется матрицей квадратичной

формы. Квадратичная форма L = называется канонической,

е сли все коэффициенты aij=0 при i≠j: L=

=