Элементарное определение

Связанные определения

В современном аксиоматическом подходе уже на основе понятия скалярного произведения векторов вводятся следующие производные понятия:

• Длина вектора, под которой понимается уже упомянутая выше его евклидова норма: (термин 'длина' обычно применяется к конечномерным векторам, однако в случае вычисления длины криволинейного пути часто используется и в случае бесконечномерных пространств).

• Углом между двумя ненулевыми векторами евклидова пространства (в частности, евклидовой плоскости) называется число, косинус которого равен отношению скалярного произведения этих векторов к произведению их длин (норм):      В случае, если пространство является псевдоевклидовым, понятие угла определяется лишь для векторов, не содержащих изотропных прямых внутри образованного векторами сектора. Сам угол при этом вводится как число, гиперболический косинус которого равен отношению модуля скалярного произведения этих векторов к произведению их длин (норм):     

• Ортогональными (перпендикулярными) называются векторы, скалярное произведение которых равно нулю. Это определение применимо к любым пространствам с положительно определённым скалярным произведением. Например, ортогональные многочлены на самом деле ортогональны (в смысле этого определения) друг другу в некотором гильбертовом пространстве.

• Пространство (вещественное или комплексное) с положительно определённым скалярным произведением называется предгильбертовым пространством.

  • При этом конечномерное вещественное пространство с положительно определённым скалярным произведением называется также евклидовым, а комплексное — эрмитовым или унитарным пространством.

• Случай, когда скалярное произведение не является знакоопределённым, приводит к т. н. пространствам с индефинитной метрикой. Скалярное произведение в таких пространствах уже не порождает нормы (и она обычно вводится дополнительно). Конечномерное вещественное пространство с индефинитной метрикой называется псевдоевклидовым (важнейшим частным случаем такого пространства является пространство Минковского). Среди бесконечномерных пространств с индефинитной метрикой важную роль играют пространства Понтрягина и пространства Крейна.

Билет 37. Определение евклидова пространства и его примеры

Определение. Вещественное линейное пространство L называется евклидовым, если в нём определена операция скалярного умножения: любым двум элементам x, yÎL сопоставлено вещественное число a = (x, y) , удовлетворяющее следующим требованиям,

1. (x, y)= (y, x) ; 2. (x + y, z) = ((x, z) + (y, z)); 3. (ax, y)= (x,ay)= a(x, y) ; 4. (x, x)> 0 для всех x ¹ q ; 5. (x, x)= 0 , если x = q .

Любое подпространство L¢ Í L - также является евклидовым пространством, так как для его элементов определено то же самое скалярное умножение.

Определение . Вещественное линейное пространство L называется евклидовым, если в нём задана положительно определённая квадратичная форма.

Примеры евклидовых пространств.

1. Геометрические векторы на плоскости L2 и в пространстве L3 с заданным скалярным произведением образуют соответствующие евклидовы пространства.

2. В арифметическом пространстве Rn мы можем ввести для элементов число

a = (x,h)= x1h1 + x2h2 + ... + xnhn = xTh. Используя свойства умножения матриц

3. В пространстве функций, непрерывных на отрезке [a,b], можно ввести скалярное произведение по формуле

Билет 38. Квадратичные формы

Определение квадратичной формы. Квадратичная форма переменных - функция

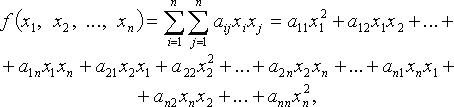
- коэффициенты квадратичной формы. Без ограничения общности считают тогда

     Если переменные принимают действительные значения и квадратичная форма называется действительной.

Матричная запись квадратичной формы

     Матрица

называется матрицей квадратичной формы, ее ранг - рангом квадратичной формы. Квадратичная форма называется невырожденной, если Главные миноры матрицы A называются главными минорами квадратичной формы. В пространстве квадратичную форму можно записать в виде где X - координатный столбец вектора В пространстве квадаратичную форму можно представить в виде где f - линейный самосопряженный оператор, матрица которого в некотором ортонормированном базисе равна A.

Билет 39.   Канонический вид квадратичной формы

Квадратичная форма называется канонической, если все т. е.

     Всякую квадратичную форму можно привести к каноническому виду с помощью линейных преобразований. Способы приведения: 1. Ортогональное преобразование пространства : где - собственные значения матрицы A.

2. Метод Лагранжа - последовательное выделение полных квадратов. Например, если

Затем подобную процедуру проделывают с квадратичной формой и т. д. Если в квадратичной форме все но есть то после предварительного преобразования дело сводится к рассмотренной процедуре. Так, если, например, то полагаем 3. Метод Якоби (в случае, когда все главные миноры квадратичной формы отличны от нуля):

Билет 40. Евклидова метрика — геометрическое расстояние между двумя точками в многомерном пространстве, вычисляемое по теореме Пифагора. Определение. Евклидова дистанция между точками p и q это длина отрезка . В Декартовых координатах, если p = (p₁, p₂,…, p_n) и q = (q₁, q₂,…, q_n) две точки в Евклидовом пространстве, длина отрезка p q равна: Линия (от лат. linea), геометрическое понятие, точное и в то же время достаточно общее определение которого представляет значительные трудности и осуществляется в различных разделах геометрии различно.Свойства прямой в евклидовой геометрии:1). Через любые две несовпадающие точки можно провести единственную прямую.2). Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или являются параллельными. 3). В трёхмерном пространстве существуют три варианта взаимного расположения двух прямых: прямые пересекаются, прямые параллельны; прямые скрещиваются. 4). Прямая линия — алгебраическая линия первого порядка: в декартовой системе координат прямая линия задается на плоскости уравнением первой степени (линейное уравнение).