§ 16.3. Понятие конечных и разделенных разностей

Пусть на равномерной сетке в узлах x₀, x₁, …, x_n заданы значения функции f(x), т. е.

y_i = f(x_i), i = 0,…, n; х_i = х_i+1 + h; i == 0,…, n.

Конечными разностями первого порядка называют величины

y_i = y_i+1y_i, i = 0,…, n1.

Разности конечных разностей первого порядка называют конечными разностями второго порядка:

²y_i = y_i+1 y_i, i = 0,…, n2.

Аналогично определяют конечные разности следующих порядков

^ky_i = ^k1y_i+1  ^k1y_i, i = 0,…, nk.

Схему вычисления конечных разностей удобно представить в виде следующего треугольника:

x₀ y_{0 y0}

x₁ y_{1 y1} ²y_{0 }³_y0

x₂ y_{2 y2} ²y_{1 }³_y1 ⁴y₀

x₃ y_{3 y3} ²y₂

x₄ y₄

Если узлы интерполяции  произвольные точки, то вводится понятие разделенных разностей.

Разделенная разность первого порядка:

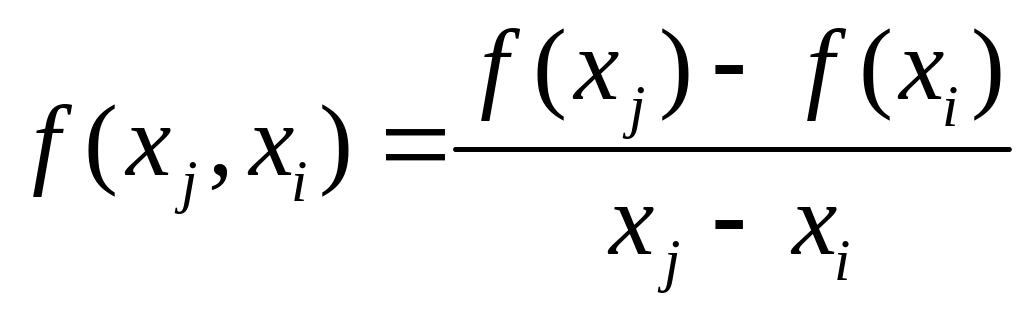
Разделенная разность второго порядка:

Разделенная разность k-го порядка выражается через разделенные разности (k1) —го порядка, следующим образом

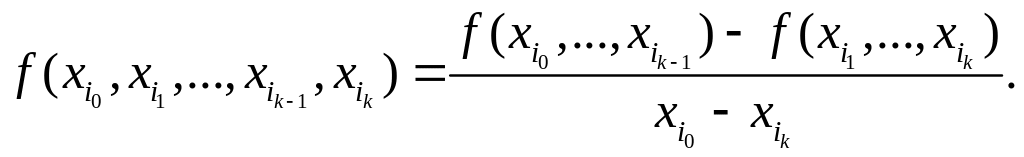
Отметим два важных свойства разделенных разностей.

1. Разделенная разность является симметричной функцией своих аргументов, т. е. значение разделенной разности не зависит от порядка перечисления узлов интерполяции, а зависит только от их значений.

2. Разделенная разность вычисляется и тогда, когда две или более точки интерполяции одинаковы.

Разделенная разность первого порядка в случае, когда одинаковы две точки, имеет вид

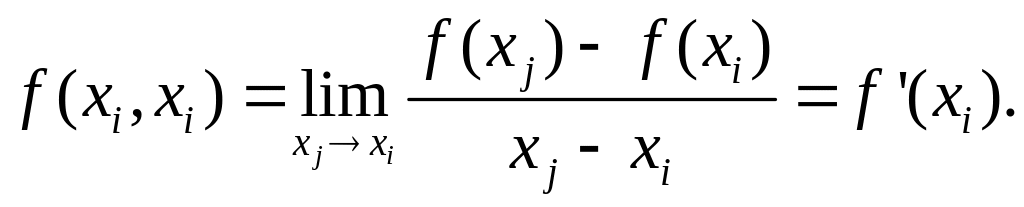
Если точка х_i, среди узлов интерполяции встречается (m+1) раз, то разделенная разность m-ro порядка на этих узлах

(16.8)

3. Если функция является многочленом степени n ( ), то ее разделенная разность n-го порядка постоянна, а разделенная разность (n+1)-го порядка обращаются в нуль (см. формулу (16.8)).

Приведем теперь схему вычисления разделенных разностей

x₀ y_{0 f(x0, x1)}

x₁ y_{1 f(x1, x2)} f(x₀, x₁, x₂) _{f(x0, x1, x2, x3)}

x₃ y_{2 f(x2, x3)} f(x₁, x₂, x₃) _{f(x0, x1, x2, x3)1} f(x₀ , x₁, x₂, x₃, x₄)

x₃ y_{3 f(x3, x4)} f(x₂, x₃, x₄)

x₄ y₄

Интерполяционная схема эйткена

Пусть функция f(x) и расположение узлов x₀, x₁, …, x_n на отрезке интерполяции [a, b] таковы, что имеет место сходимость процесса интерполяции, т.е. R_n(x)0 при n. Пусть требуется найти не общее выражение L_n(x), а лишь его значения при конкретных x, т.е. решается частная задача вычисления отдельных приближенных значений функции f(x) с помощью вычисления соответствующих им значений интерполяционного многочлена Лагранжа L_n(x). Для построения эффективного способа решения такой частной задачи интерполяции учтем следующее:

1. использование многочлена Лагранжа в виде (2.3) неудобно из-за его громоздкости, что ведет к большим вычислительным затратам;

2. заранее не известно, многочлены какой степени нужно использовать для интерполирования данной функции с требуемой точностью. А постепенное улучшение точности за счет вычислений L_n(x) с большим показателем степени n невыгодно, т.к. L_n-1(x) плохо перестраивается в L_n(x);

3. функция f(x) задается таблицей своих приближенных значений. Процесс сходимости L_n(x) к f(x) при больших значениях n будет нарушен влиянием на результат исходных ошибок.

Построим вычислительную схему для получения приближенного значения сеточной функции f(x) в заданной точке , в основу которой будет положена интерполяция Лагранжа на сетке узлов x₀, x₁, …, x_n. Организация вычислений по этой схеме будет иметь итерационный характер. Каждый шаг заключается в вычислении некоторого определителя второго порядка.

Пусть даны две точки на кривой y=f(x): (x₀, y₀) и (x₁, y₁). Построим функцию P_0,1(x):

.

.

Т.е. P_0,1(x) совпадает с интерполяционным многочленом Лагранжа первой степени, построенным по двум данным точкам (сравните с 2.3).

Построим через определитель функцию P_1,2(x) для точек (x₁, y₁), (x₂, y₂):

.

.

Она тоже является многочленом Лагранжа первой степени, построенным по двум точкам (x₁, y₁) и (x₂, y₂).

Если на кривой y=f(x) заданы три точки (x₀, y₀), (x₁, y₁), (x₂, y₂), то, используя введенные линейные функции P_0,1(x) и P_1,2(x) образуем новую функцию:

.

Покажем, что эта функция есть многочлен второй степени. Учитывая, что

P_0,1(x₀)=P_1,2(x₁)=y₀,

P_0,1(x₁)=y₁, P_1,2(x₂)=y₂,

подставляя в P_0,1,2(x) поочередно значения x=x₀, x₁, x₂, получим:

P_0,1,2(x₀)=y₀; P_0,1,2(x₁)=y₁; P_0,1,2(x₂)=y₂.

Т.о., функция P_0,1,2(x) – это многочлен второй степени, решающий задачу параболической интерполяции по трем точкам (x₀, y₀), (x₁, y₁), (x₂, y₂). Но такой многочлен единственный, следовательно, P_0,1,2(x)=L₂(x), где L₂(x) – многочлен Лагранжа.

Продолжая процесс рассуждения, получим рекуррентное задание последовательности интерполяционных многочленов Лагранжа, которое составляет суть интерполяционной схемы Эйткена:

, ()

где i=1, 2, …, n и по определению P₀(x)=y₀, P₁(x)=y₁.

Схема Эйткена легко реализуется на ЭВМ. Организация вычислений по формуле (3.1) должна быть такова, что если заранее неизвестна степень интерполяционного многочлена, который нужно использовать для вычисления y(x), то должно происходить постепенное повышение степени k интерполирующих ее многочленов за счет подключения новых узлов. Счет ведется до тех пор, пока идет уточнение приближенного значения y(x).

Об этом можно судить по уменьшению величины |P_{i, i+k-1}(x)-P_{i, i+k}(x)| при увеличении k и подходящем фиксировании i.

Пример. Пусть некоторая функция y=y(x) задана таблицей своих значений, округленных до двух знаков после запятой:

xi	0.0	0.2	0.4	0.6	0.8	1.0	1.2	1.4
yi	1.00	1.02	1.08	1.12	1.34	1.54	1.81	2.15

Рассмотрим процесс вычисления двух значений этой функции по схеме Эйткена в точках: а) ; б) . Результаты промежуточных вычислений (в которых один знак запасной) сведем в табл. 3.1, 3.2. Числа в столбцах, помеченных посредством , представляют собой значения многочленов Лагранжа k-ой степени, построенных по узлам от i-го до (i+k)-го рекуррентно по формуле:

, (3.2)

где k=1, 2, …, , в соответствии с интерполяционной схемой Эйткена. Порядок получения этих значений показан проставленными в каждой клетке номерами.

8