Лекция 14.

ОСНОВНЫЕ ИТЕРАЦИОННЫЕ МЕТОДЫ

§ 14.1. Метод итераций для системы уравнений.

Пусть необходимо найти решение системы уравнений

f₁(х₁, х₂, …, х_n) = 0,

f₂(х₁, х₂, …, х_n) = 0, (14.1)

…

f_n(х₁, х₂, …, х_n) = 0.

Применение метода итераций требует приведения этой системы к виду:

х₁=₁(х₁, х₂, …, х_n),

х₂=₂(х₁, х₂, …, х_n),

…

х_n=_n(х₁, х₂, …, х_n).

В общем случае это можно сделать так же, как и для одного уравнения:

х_i = х_i +h f_i(х₁, х₂, …,); i = 1,2, .., n.

Отсюда

_i(х₁, х₂, …, х_n) = х_i +h f_i(х₁, х₂, …,).

Параметр h здесь также выбирается из условия сходимости метода. Метод итераций для системы уравнений приобретает вид

(14.2)

Запишем метод итераций в векторном виде. Обозначим

х = (х₁,х₂, ..., х_n)^т;  = (₁, ₂, …, _n).

Тогда

x^(k+1) =  (x^(k)), k = 0,1,2 ... .

Рассмотрим, как ведет себя погрешность на итерациях метода. Обозначим через  вектор погрешности. Очевидно, что

x^(k) = x*+  ^(k),

где х*  точное решение. Как и для одномерного случая можно получить, что

 ^(k+1) = A  ^(k),

где

Теорема 14.1. Пусть система уравнений (14.1) приведено к виду х= (х) таким образом, что вектор-функция  (х) дифференцируема и и все собственные значения матрицы A по модулю меньше единицы, т.е. |_i |<1, i = 1,2, .., n,

Тогда последовательность {x_k}  х*.

§ 14.2. Правило Зейделя.

Возвратимся к записи метода итераций для системы уравнений в координатном виде (14.1). Сходимость итерационного процесса несколько улучшается, если при расчете функции _i использовать вычисленные к этому моменту времени компоненты вектора x, а остальные компоненты вектора х взять с предыдущего шага:

§ 14.3. Метод Ньютона.

Рассмотрим уравнение (13.1), х*  корень, х[а,.b]. Пусть найдено k-е приближение х^(k). Представим х^(k+1)= х^(k)+х. Разложим в ряд Тейлора в окрестности точки х^(k) функцию f(x):^:

f(x) = f(х^(k)+х) = f(х^(k)) + f'(х^(k))x + 0(x²).

Полагая, что x^(k+1) = x*  решение, ограничившись двумя членами разложения, получим

f(х^(k)) + f'(х^(k))x = 0.

Отсюда x =  f(х^(k))/ f'(х^(k)), и итерационное правило метода Ньютона примет вид

х^(k+1) = х^(k)  f(х^(k))/ f'(х^(k)), k = 1,2, ... . (14.3)

Здесь х⁽⁰⁾ — начальное приближение.

Рис. 14.1

Геометрический смысл правила Ньютона весьма прост. В плоскости ху построим график функции у = f(x) (см. рис. 14.1).

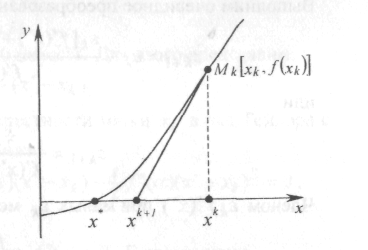
Точное решение х* будет точкой пересечения этого графика с осью абсцисс. Рассмотрим на этом графике точку M_k(х^(k),f(х^(k))) проведем касательную, проходящую через точку M_k. Точку пересечения касательной с осью х обозначим х^(k+1).

Геометрическая интерпретация правила Ньютона может быть сформулирована следующим образом: последующее приближение х^(k+1) ищется как точка пересечения с осью абсцисс касательной к функции f(x) в предыдущей точке х^(k).

Теорема 14.2. Пусть функция f(x) удовлетворяет условиям

Тогда если члены последовательности {x_k}, определяемые методом Ньютона (14.3), при любом фиксированном k = 1,2, ... принадлежат отрезку [а,b] и эта последовательность сходится на [а,b] к корню х* уравнения (13.1), то справедливы неравенства:

(Первое из этих неравенств позволяет считать (14.3) методом второго порядка, а второе, являясь апостериорной оценкой погрешности, может служить в качестве критерия останова процесса вычислений).