§7.6.Формула Тейлора для функций нескольких переменных.

Пусть ,

, .

Теорема. Пусть функция имеет в шаре непрерывные частные производные всех порядков до –го включительно. Тогда для каждой точки существует действительное число такое, что справедливо равенство

(1)

которое называют формулой Тейлора с остаточным членом в форме Лагранжа. Здесь

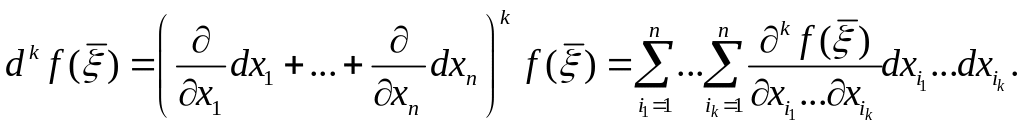
□ Если , то по причине симметрии шара точка , а поэтому отрезок Рассмотрим функцию

которая определена на и имеет производные до порядка включительно. Действительно, пользуясь правилом вычисления производной сложной функции, имеем

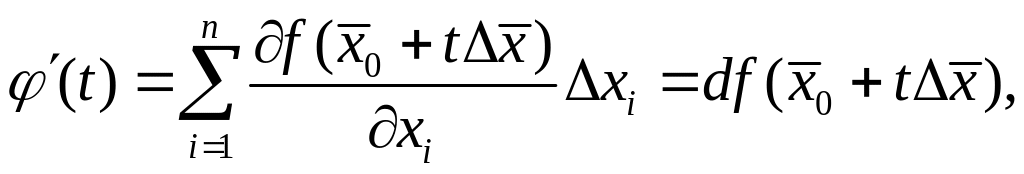
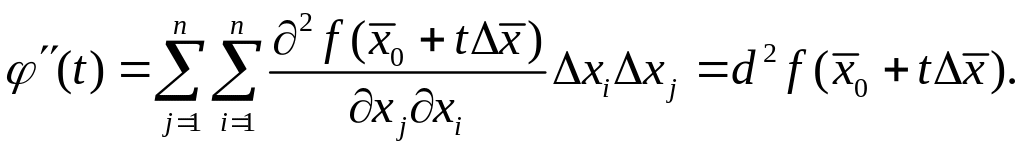
По индукции получаем, что имеют место формулы

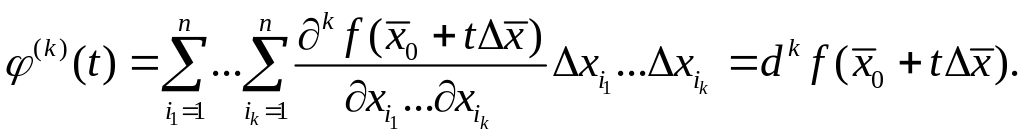(2)

Используя для функции формулу Тейлора с остаточным членом в форме Лагранжа в окрестности точки , получаем

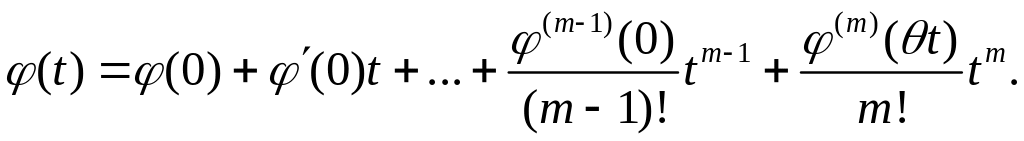
Взяв здесь , получаем

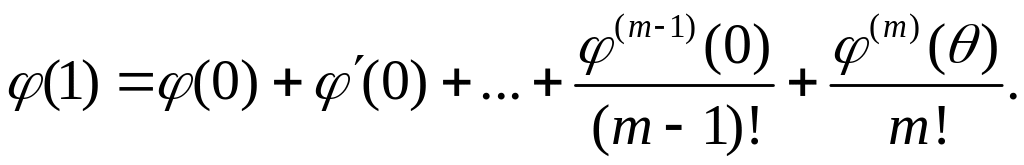
Если подставить в это равенство выражение производных из (2) при , получим формулу (1). ■

Замечание. Если выполняются условия теоремы, то формула Тейлора может быть записана с остаточным членом ву форме Пеано

. (3)

§7.7. Экстремум функций нескольких переменных.

Пусть функция определена в области .

Будем говорить, что функция имеет в точке локальный максимум (минимум), если существует такой шар , что выполняются неравенства . Точки локального минимума и локального максимума называют точками локального экстрэмума.

Теорема 1 (неабходимое условие экстремума). Если функция является дифференцируемой в точке и имеет в этой точке локальный экстремум, то

□ Рассмотрим функцию

определённую в некоторой окрестности точки . Поскольку имеет в точке локальный экстремум, то , т.е. тоже имеет локальный экстремум при . На основании теоремы Ферма . Но 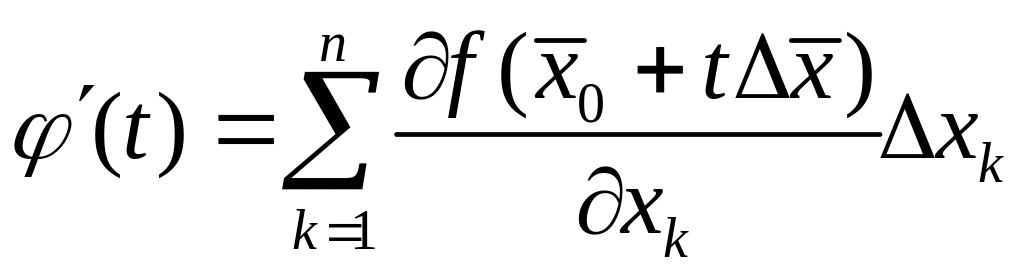, а поэтому .

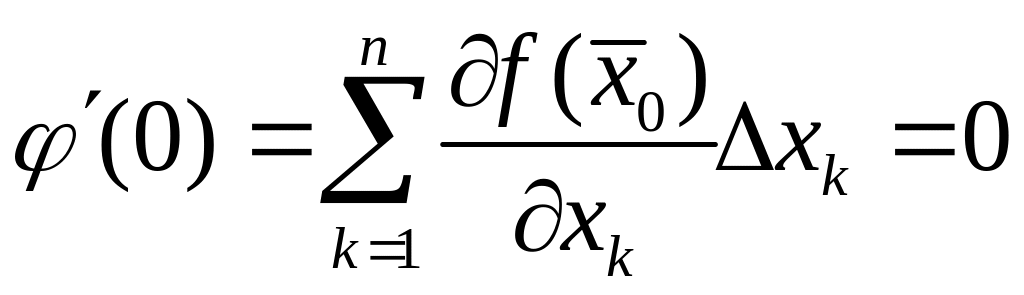Поскольку это равенство имеет место для произвольных , то отсюда следует, что

. ■

Если функция является дифференцируемой в точке и , то точку называют стационарной. Согласно теореме 1 точка экстремума дифференцируемой функции является стационарной. Обратное утверждение неверно. Стационарная точка может и не быть точкой экстрэмума. Например, для функции точка является стационарной, но не является точкой экстремума (почему?).

Дальше нам потребуются некоторые сведения о квадратичных формах.

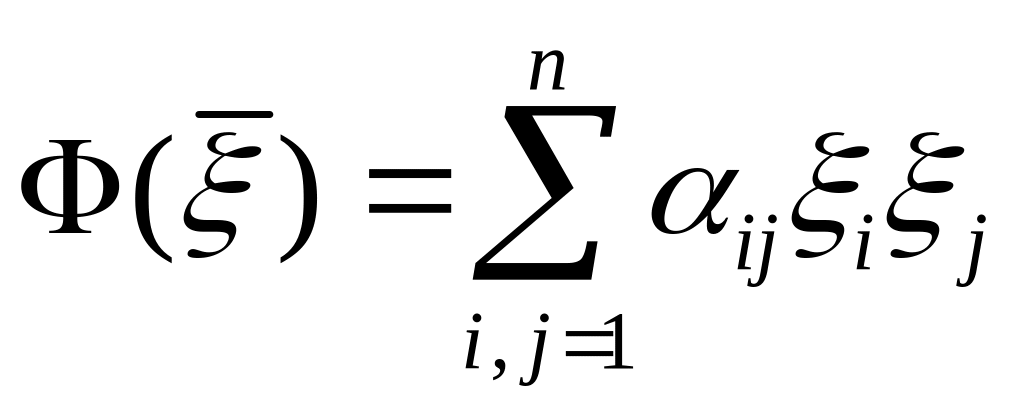Если , то функцию называют квадратичной формой переменных . Здесь .

Квадратичную форму называют положительно определённой, если ; отрицательно определённой, если ; неопределённой, если .

В курсе алгебры рассматривается Критерий Сильвестра положительной определённости квадратичной формы: квадратичная форма является положительно определённой, если и тольки если все главные миноры её матрицы положительные, т.е.

Отметим, что квадратичная форма будет отрицательно определённой только в том случае, если квадратчная форма – положительно определённая. Поэтому для отрицательной определённости квадратичной формы необходимо и достаточно, чтобы .