4.4. Условный экстремум

Пусть требуется найти максимум или минимум функции z = f(x, y) при условии, что x или y связаны уравнением (x, y) = 0, которое является ограничением на значения переменных (его называют также уравнением связи).

Иногда можно решать данную задачу прямым методом, который сводит ее к задаче на безусловный экстремум. Суть этого метода состоит в том, что из уравнения (x, y) = 0 выражаем одну переменную через другую, например y через x, т.е. получаем зависимость y = y(x). Теперь можем записать z = f(x, y(x)), и затем уже находить безусловные экстремумы функции одной переменной f(x, y(x)). Однако это не всегда осуществимо.

Решая задачу на условный экстремум, зачастую не выражают явно y через x (или наоборот), а используют метод множителей Лагранжа. Опишем его.

Составим вспомогательную функцию (функцию Лагранжа)

L(x, y, ) = f(x, y) + (x, y),

где числовой коэффициент  называется множителем Лагранжа и он играет вспомогательную роль. Для F(x, y, ) как для функции трех переменных выписываются необходимые условия экстремума без ограничений:

L_x = + = 0, L_y = + = 0, L_ = (x, y) = 0

(последнее равенство есть в точности уравнение связи). Из этой системы находится одно или несколько решений (x^*, y^*, ^*), а если не включать ^*, то получится стационарная точка (x^*, y^*) исходной задачи. Затем найденные точки (x^*, y^*) проверяются на наличие в них экстремума и его вид – максимум или минимум. Проверка осуществляется с использованием достаточных условий экстремума при наличии ограничений на переменные. Часто из существа задачи легко решается вопрос, с максимумом или минимумом имеем дело.

Метод Лагранжа допускает обобщение на функции большего числа переменных и связей. Задача определения экстремума функции f(x₁,…, x_n) при наличии ограничений _i(x₁,…, x_n) = 0, i=1,…, m; m < n, сводится к нахождению безусловного экстремума для функции Лагранжа:

L(x₁,…, x_n, ₁,…, _m) = f(x₁,…, x_n) + ₁₁(x₁,…, x_n) + … + _m_m(x₁,…, x_n),

где _i (i=1,…,m) – постоянные множители. Система для определения стационарных точек (x₁^*,…, x_n^*) и m множителей Лагранжа ₁^*,…,_m:

= + ₁+ … + _m = 0 (j=1,…,m);

=  _i(x₁,…, x_n) = 0 ( i = 1,…, m)

(последние m равенств суть уравнения связей).

Вопрос о существовании и виде условного экстремума в ряде случаев решается исследованием знака выражения

(dx₁,…, dx_n) , (1)

где (X^*, ^*) – краткое обозначение набора координат стационарной точки и соответствующих ей значений множителей Лагранжа, т.е.

(X^*, ^*) = (X^*= (x₁^*,…, x_n^*), ^*=(₁^*,…, _m^*));

в дальнейшем (X^*, ^*) будем называть стационарными точками функции Лагранжа. Отметим, что наборы (dx₁,…, dx_n) выбираются не произвольным образом, а должны удовлетворять ограничениям

dx₁ + … + dx_n =0, i =1,…,m,

причем частные производные для функций _i(x₁,…, x_n) в этих m уравнениях вычисляются в стационарной точке (x₁^*,…, x_n^*). Если для всевозможных ненулевых наборах (dx₁,…, dx_n), удовлетворяющих указанным ограничениям, величина (1) принимает лишь отрицательные значения, то в (x₁^*,…, x_n^*) имеется условный максимум; если положительные – то минимум. В этом заключаются достаточные условия экстремума при наличии ограничений.

Пример 1. Исследовать на экстремум функцию f(x, y) = 2x + 3y, если имеется ограничение на значения переменных x² + y² =1.

Решение. Здесь (x, y) = x² + y² – 1 = 0. Ищем стационарные точки функции Лагранжа, которая имеет вид

L(x, y, ) = 2x + 3y + (x² + y² – 1)

Решая систему трех уравнений

L_x = 2 + 2x = 0, L_y = 3 + 2y = 0, L_ = x² + y² – 1 = 0,

получаем x = –1/, у = –3/(2) и + –1 = 0. Имеем ₁^*= , ₂^*= – . Итак, функция L(x, у, ) обладает двумя стационарными точками

A(x₁^*= – , y₁^*= – , ₁^*= ),

B(x₂^*= , y₂^*= , ₂^*= – ).

Рассмотрим точку A( – , – , ). Здесь

= = .

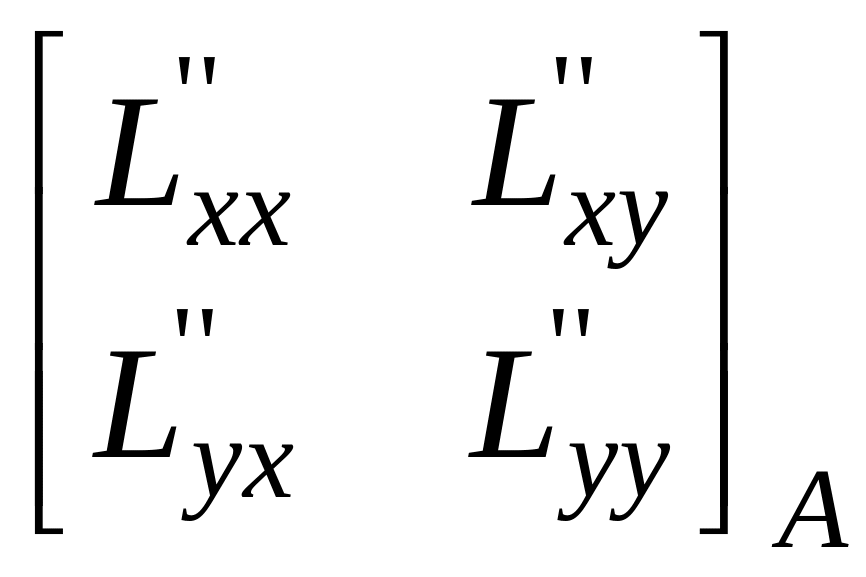Кроме того, ввиду = 2x, = 2y, имеем

( – , – )dx + ( – , – ) = –dx – dy,

откуда dy = –dx. Имеем

(dx, dy) = (dx, –dx) =

= (dx, – dx) = ( + )dx² > 0, если dx  0.

Итак, ( – , – ) – точка минимума.

Исследуем точку B( , , – ). Здесь

= = .

Так как = 2x, =2y, то

( , )dx + ( , ) dy = dx + dy = 0,

откуда dy = –dx. Имеем

(dx, dy) =(dx, –dx) =

= (–dx, dx) = –( + )dx² <0,если dx  0.

Итак, ( , ) – точка максимума.

Пример 2. Доказать, что площадь полной поверхности прямоугольного параллелепипеда данного объема V имеет минимум тогда, когда параллелепипед является кубом.

Решение. Пусть x, y, z – размеры параллелепипеда. Естественно, x, y, z > 0.

Составляем функцию Лагранжа: L = xy + xz + yz + (xyz – V). Получаем систему четырех уравнений

L_x = y + z + уz = 0, L_y = x + z + xz = 0, L_z = x + y + xy = 0,

L_ = xyz – V = 0.

Решая систему, получим единственную стационарную точку функции Лагранжа

P(x^*= , y^*= , z^*= , ^*= –2V^–1/3).

Поскольку стационарная точка в рассматриваемой задаче единственна, то она как раз и будет соответствовать прямоугольному параллелепипеду с наименьшей площадью полной поверхности. При этом все 3 размера одинаковы, т.е. этот прямоугольный параллелепипед – куб.