
4. Функции многих переменных
4.1. Понятие функции многих переменных
Пусть
![]() –
некоторое множество в
–
некоторое множество в
![]() -мерном
евклидовом пространстве
-мерном
евклидовом пространстве
![]() и каждой точке
и каждой точке
![]() поставлено в соответствие определенное
действительное число
поставлено в соответствие определенное
действительное число
![]() .
В этом случае говорят, что задана функция
переменных. Для обозначения функции
n переменных
используется та же символика, что и для
случая функции одного переменного. Так,
в частности, пишут
.
В этом случае говорят, что задана функция
переменных. Для обозначения функции
n переменных
используется та же символика, что и для
случая функции одного переменного. Так,
в частности, пишут
![]() ,
,
где
![]() – вектор переменных
– вектор переменных
![]() ,
т.е.
,
т.е.
![]() ,
при этом множество
называют областью определения функции.
,
при этом множество
называют областью определения функции.
Линией (поверхностью) уровня функции
![]() ,
,
называется множество
![]()
точек области
определения, в которых функция постоянна.
Здесь
![]() ,
,
![]() .
.
Если рассматривается функция двух переменных, то множества, на которых функция не меняет своих значений, представляют собой, в общем случае, плоские линии. Если же исследуется функция трех и большего числа переменных, то эти множества уже являются поверхностями (гиперповерхностями) в соответствующих пространствах.
Линии (поверхности) уровня у функции не пересекаются.
4.2. Частные производные
Пусть функция
![]() ,
,
![]() ,
определена в окрестности точки
,
определена в окрестности точки
![]() .
.
Определение 1.
Частной производной
![]() функции
в точке
функции
в точке
![]() по переменной
по переменной
![]() ,
,
![]() ,
называется производная функции
,
называется производная функции
![]() одного переменного
,
вычисленная в точке
одного переменного
,
вычисленная в точке
![]() :
:
![]() .
.
Таким образом, при вычислении частной производной все переменные фиксируются и рассматриваются как параметры, за исключением того переменного, по которому ищется производная.
Вектор
![]() ,
составленный из частных производных,
называется градиентом функции в точке
,
составленный из частных производных,
называется градиентом функции в точке
![]() .
.
Градиент функции определяет направление наибольшего роста функции в рассматриваемой точке.
Заметим, что результаты, изложенные для плоского случая, естественным образом переносятся на случай функции от любого числа переменных.
Пусть функция
![]() определена в окрестности точки
определена в окрестности точки
![]() ,
имеет частные производные
,
имеет частные производные
![]() и
и
![]() ,
и эти производные как функции,
рассматриваемые в окрестности точки,
в свою очередь, также имеют частные
производные. Эти производные называются
частными производными второго порядка:
,
и эти производные как функции,
рассматриваемые в окрестности точки,
в свою очередь, также имеют частные
производные. Эти производные называются
частными производными второго порядка:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
При этом
частные производные
![]() и
и
![]() называют смешанными производными.
Заметим, что аналогичным образом
определяются частные производные
порядка выше второго функций двух и
большего числа переменных.
называют смешанными производными.
Заметим, что аналогичным образом
определяются частные производные
порядка выше второго функций двух и
большего числа переменных.
Теорема.
Если функция
определена вместе с частными производными
первого и второго порядков в окрестности
точки
,
смешанные производные
и
непрерывны в точке
![]() ,
то смешанные производные в этой точке
совпадают:
,
то смешанные производные в этой точке
совпадают:
![]() =
=![]() .
.
Задача. Найти все
частные производные до второго порядка
включительно у функции
![]() .
.
Решение. Вычислим частные производные первого порядка:
![]() ,
,
![]() .
.
Затем посчитаем частные производные второго порядка по одноименным переменным:
![]()
![]() ,
,
![]() .
.
Вычисляя смешанные производные
![]()
![]() ,
,
![]()
,
убеждаемся в справедливости теоремы.
Матрица
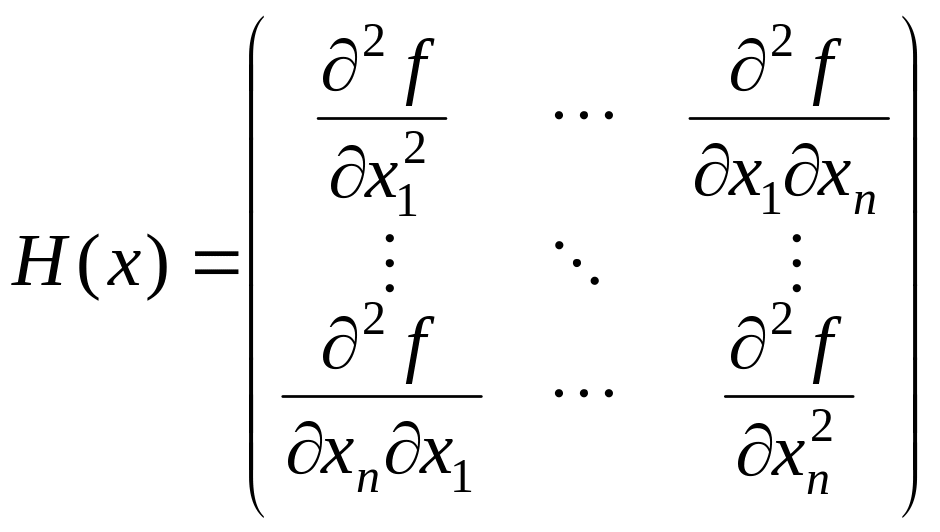 ,
,
составленная из вторых производных, называется матрицей Гессе.
4.3. Экстремумы функций многих переменных
Определение. Пусть функция f(P) = f(x1,…, xn) определена в окрестности точки P0 = (x10,…, xn0). Если f(P0) = f(x10,…, xn0) > f (P) в этой окрестности, то функция f(P) имеет максимум в P0 (если f(P0) < f(P), то будет, соответственно, минимум).
Точка P0 называется стационарной, если в ней все частные производные равны нулю: = 0, i=1,…, n.
Необходимое условие экстремума. Дифференцируемая функция f(x1,…, xn) может достигать экстремума (максимума или минимума) лишь в стационарной точке P0.
Равенство нулю частных производных не является достаточным для экстремума. Например, пусть f(x, y) = x2y3; f /x = 2xy3, f /y = 3x2y2, и в точке P0(0,0) справедливо f /x = f /y = 0. Однако в любой окрестности P0 функция f(x,y) принимает как положительные (при x > 0, y > 0), так и отрицательные (при x > 0, y < 0) значения, т.е. экстремума нет.
Достаточное условие безусловного экстремума. Функция f(P) в точке P0 имеет минимум, если
![]() (P0)
> 0,
(P0)
> 0,
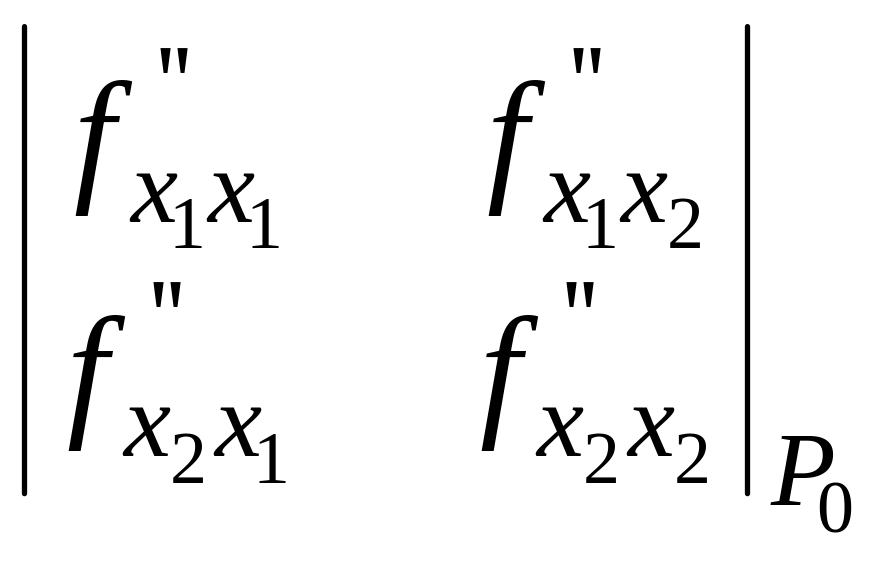 > 0, …,
> 0, …,
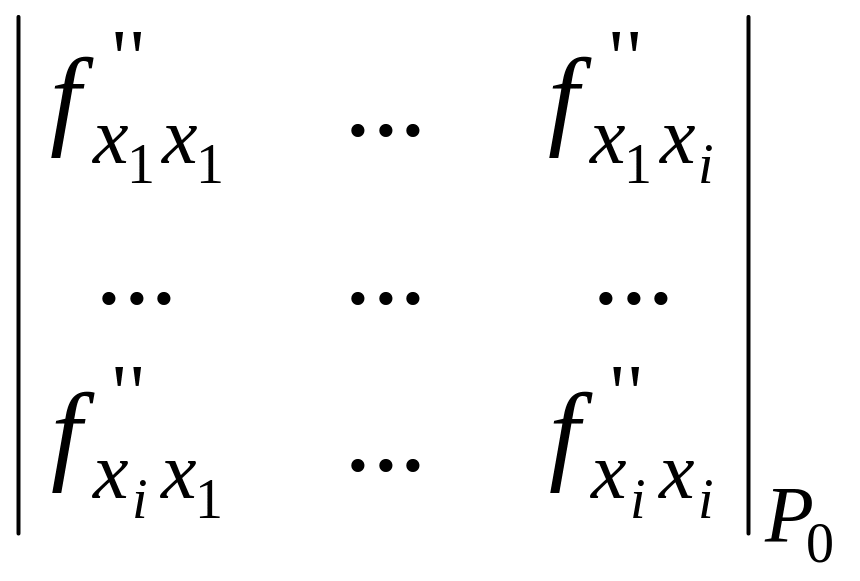 >
0, … ,
>
0, … ,
 >
0;
>
0;
Функция f(P) в точке P0 имеет максимум, если
(P0) < 0, > 0,
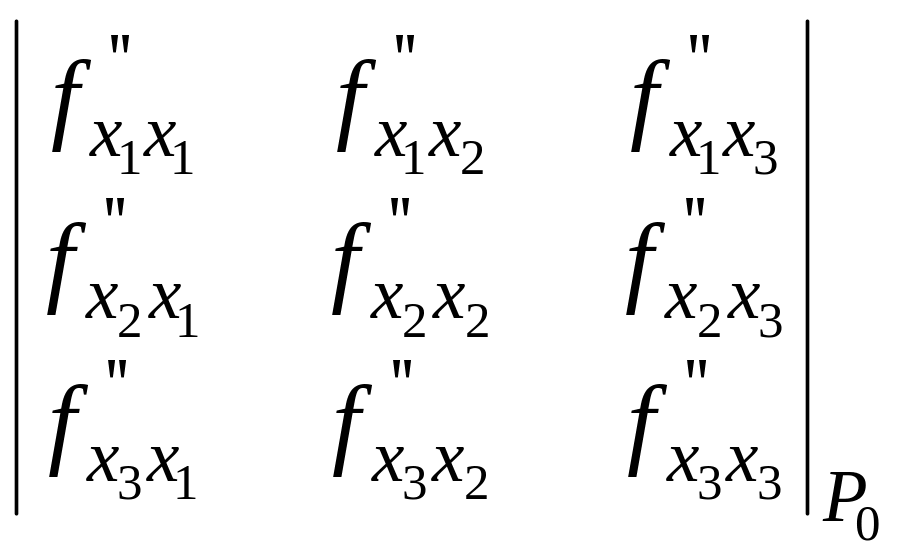 <
0, … , (–1)n
>
0,
<
0, … , (–1)n
>
0,
(последний определитель положительный, если n четное; отрицательный – если n нечетное).
Для функции f(x, y) двух независимых переменных в стационарной точке P0 = (x0, y0) имеем следующие условия. Пусть
A =
![]() (P0),
B =
(P0),
B =![]() (P0),
C =
(P0),
C =
![]() (P0);
(P0);
тогда в точке P0:
минимум, если A > 0, AC – B2 > 0;
максимум, если A < 0, AC – B2 > 0.
Заметим, что экстремум в точке P0 нет, если AC – B2 < 0.
Пример 1. Исследовать на экстремум функцию f(x, y) = x3 + y3 – 3xy.
Решение. Найдем вначале все стационарные точки. Имеем систему уравнений
о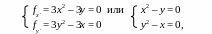 ткуда
получаем две стационарные точки P1
= (1, 1), P2 = (0,
0). Точка P1 –
точка минимума, поскольку
ткуда
получаем две стационарные точки P1
= (1, 1), P2 = (0,
0). Точка P1 –
точка минимума, поскольку
A = (P1) = 6x|P1 = 6, B = (P1) = –3, C = (P1) = 6y|P1 = 6.
и
A
> 0,
 =
=
![]() =
AC – B2
= 66
– 32 = 27 > 0.
=
AC – B2
= 66
– 32 = 27 > 0.
Теперь рассмотрим точку P2. Имеем
A = (P2) = 0, B = (P2) = –3, C = (P2) = 0.
Откуда AC – B2 = –9 < 0, т.е. в точке P2=(0, 0) экстремума нет. Заметим, это видно из того, что если взять точку (, 0), > 0, то f(, 0) = 3 > 0, а для точки (–, 0) справедливо f(–, 0) = –3 < 0, – т.е. в сколь угодно малой окрестности (0, 0) функция f(x, у) может принимать как положительные, так и отрицательные значения.
Пример 2. Исследовать на экстремум функцию
f(x, y, z)= x2 + y2 + z2 + 2x + 4y – 6z.
Решение. Ищем стационарные точки. Решая систему трех уравнений
fx = 2x + 2 = 0, fy = 2y + 4 = 0, fz = 2z – 6 = 0,
получаем единственную стационарную точку P(–1, –2, 3). Используя достаточное условие экстремума:
(P)
= 2 > 0,
![]() =
=
![]() = 4 > 0,
= 4 > 0,
 =
=
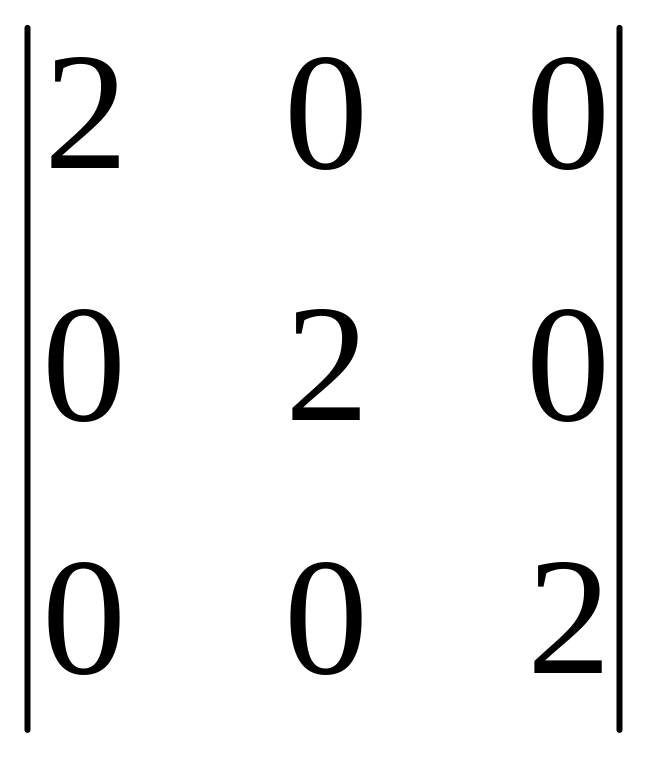 = 8 > 0.
= 8 > 0.
Выполнены все условия минимума для точки P(–1,–2,3).
