22. Понятие закона распределения случайной величины. Законы распределения дискретных случайных величин. Ряд распределения. Практический пример.

Законы распределения случайных величин

Всякое соотношение, которое устанавливает связь между возможными значениями случайной величины и вероятностями этих значений, называют законом распределения этой СВ.

Изучение законов распределения начнем с дискретных случайных величин.

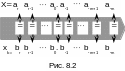
Ряд распределения. Обозначим дискретную СВ как X, а набор ее отсчетов – как x₀, x₁,…, x_n. Исход случайного эксперимента – событие X=x_k характеризуется вероятностью P(X=x_k)=p_k. Факт равенства чисел X=x_k устанавливают путем последовательного сравнения цифр в одноименных разрядах записей X и x_k (см. рис. 8.2). Если имеет место a_i=b_i для всех i=r,r-1,¼,-m, то числа X и x_k равны.

Сопоставим каждому отсчету x_k случайной величины X вероятность p_k. В результате получим закон распределения дискретной СВ X. Самой простой формой записи закона распределения дискретной случайной величины является таблица, в первой строке которой перечисляются ее отсчеты x_k, а во второй – вероятности p_k. Такую таблицу {x_k,p_k} и называют рядом распределения.

Очевидно, что события X=x_k, k= образуют полную группу, и поэтому .

Пример. Стрелок производит три выстрела по мишени. Вероятность попадания в мишень при каждом выстреле равна 0.6. Построить ряд распределения для числа попаданий в мишень при трех выстрелах.

Обозначим как Z дискретную случайную величину – число попаданий в мишень. Набор ее значений: z₀=0, z₁=1, z₂=2, z₃=3. Опыт укладывается в схему Бернулли. Поэтому вероятность события Z=z_k вычисляем по формуле Бернулли:

p₀= =0.4³=0.064, p₁= = ´0.6´0,4²=0.288,

Таблица 8.1
zk	0	1	2	3
pk	0.064	0.288	0.432	0.216

p₂= = ´0.6²´0.4=0.432, p₃= =0.6³=0.216.

Теперь составляем табл.8.1 – ряд распределения случайной величины Z.

22. Основные характеристики дискретных случайных величин. Написать и пояснить формулы математического ожидания, дисперсии и среднеквадратического отклонения. Практический пример.

Числовые характеристики случайных величин

Закон распределения той или иной случайной величины описывает ее с вероятностной точки зрения в полной мере. Любые задачи, связанные со случайными величинами, могут быть решены с помощью законов распределения. Однако далеко не все задачи подобного рода требуют для их решения такой тяжелой артиллерии. Бывает достаточно оперировать с компактными характеристиками, отражающими самые существенные особенности случайных величин. Для этих целей и служат числовые характеристики случайных величин. В первую очередь, это математическое ожидание и дисперсия случайной величины.

Математическое ожидание МО характеризует местоположение случайной величины на числовой оси. Это своего рода центр тяжести всего массива ее отсчетов. Обозначают математическое ожидание случайной величины X как M[X], либо как m_x. Математическое ожидание случайной величины X называют еще и ее средним.

Дисперсия случайной величины X характеризует разброс (рассеяние, распределение) ее отсчетов на числовой оси относительно математического ожидания m_x этой случайной величины. Обозначают дисперсию случайной величины X как D[X] или как D_x.

Пусть математическое ожидание m_x случайной величины X задано. Тогда дисперсия случайной величины вычисляется так:

D[X]M[X²](m_x)², (8.8)

а именно, дисперсия СВ равна разности между ее средним квадратом и квадратом ее среднего.

Центрированной случайной величиной X_Ц, соответствующей X, называется отклонение X от ее математического ожидания m_x:

X_ЦXm_x.

Геометрически переход от X к X_Ц означает перенос начала координат на числовой оси в точку m_x. Иногда удобнее бывает вычислять дисперсию по формуле

D[X]D_xM[(Xm_x)²M[(X_Ц)²], (8.9)

то есть дисперсией случайной величины X называют математическое ожидание квадрата соответствующей ей центрированной случайной величины X_Ц.

Отметим существенный факт. Если размерность математического ожидания m_x совпадает с размерностью самой случайной величины X, то дисперсия имеет размерность квадрата размерности случайной величины. Удобнее было бы оперировать с числовыми характеристиками одной размерности. Для этого из дисперсии извлекают корень квадратный. Полученную величину называют средним квадратическим отклонением СКО случайной величины X и обозначают как _x:

_x . (8.10)

Размерность СКО совпадает с размерностью случайной величины.

Рассмотрим числовые характеристики дискретных случайных величин.

МО дискретной случайной величины вычисляют так:

M[X]m_xx₀p₀x₁p₁x_np_n . (8.11)

Как видим, математическое ожидание дискретной случайной величины – это взвешенная сумма ее отсчетов, когда каждый отсчет x_k умножается на свою вероятность p_k (на свой вес), и полученные произведения суммируются.

Дисперсия дискретной СВ по формуле (8.8) вычисляется так:

D_x . (8.12)

Таблица 8.2
qk	1	2	5	7
pk	0.2	0.3	0.4	0.1
Таблица 8.3
rk	3	3	7	12
pk	0.2	0.5	0.2	0.1

Пример. В табл. 8.2 и 8.3 заданы законы распределения дискретных величин Q и R, соответственно. Найдем числовые характеристики этих случайных величин.

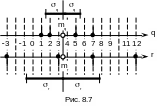На рис. 8.7 показано размещение отсчетов случайных величин Q и R на числовой прямой. Сначала по формуле (8.11) вычисляем математические ожидания для случайных величин Q и R:

m_q10.220.350.470.13.5 (см. рис. 8.7),

m_r30.230.570.2120.13.5 (см. рис. 8.7).

Как оказалось, Q и R имеют одинаковые средние: m_qm_r3.5. Но легко заметить (рис. 8.7), что отсчеты R относительно m_r разбросаны сильнее, чем отсчеты Q относительно m_q.

По формулам (8.12) и (8.10) вычислим дисперсии и СКО для случайных величин Q и R:

D_q1²0.22²0.35²0.47²0.13.5²4.05,

_q2.01 (рис. 8.7),

D_r(3)²0.23²0.57²0.212²0.13.5²18.25,

_r4.27 (рис. 8.7).

Как видим, большему разбросу отсчетов случайной величины отвечают большие дисперсия и СКО.

Пример. Найти числовые характеристики дискретной случайной величины Z (табл. 8.1).

Действуя по формуле (8.11), находим МО для дискретной СВ Z:

M[z]m_z00.06410.28820.43230.2161.8.

Значит, центром тяжести для точек z{0, 1, 2, 3} из (табл. 8.1) будет точка m_z1.8.

Действуем по формулам (8.10) и (8.10):

D_z0²0.0641²0.2882²0.4323²0.2161.8²0.72.

_z0.85.