12. Среднее квадратическое отклонение дискретной случайной величины: определения, свойства, формулы для вычисления.

Среднее квадратическое отклонение дискретной случайной величины Х наз-ется квадратный корень из ее дисперсии:

Св-ва дисперсии:

1. D(X)≥0 ¥; D(C)=0, где С - постоянная величина;

2. D(СХ)=С*D(Х), где С – постоянная величина;

3. D(Х₁+Х₂+…+Х_п)=D(Х₁)+D(Х₂)+…+D(Х_п), если Х₁,Х₂,…Х_п – независимые случайные величины взаимно независимы;

4. D(X)=M(X²)-(M(X))²

5. Для Дискретной случайной величины Х, заданной табл.1, справедливо равенство:

Для Дискретной случайной величины , заданной табл.2, справедливо равенство:

6. Для Дискретной случайной величины Х и У, заданных, соответственно, табл.1 и 3, связаны равенством: D(Y) = D(X);

7. Для Дискретной случайной величины Х и Z, заданных, соответственно, табл.1 и 4, связаны равенством: D(Z) = b² * D(X);

8. Для Дискретной случайной величины Х, имеющие биномиальное распределение, равна произведению числа испытаний на вероятность появления и не появления события в одном испытании: D(Х) = пр(1 – p).

13. Ряды распределения, их разновидности.(196,200)

???

14. Непрерывная случайная величина: определение, плотность распределения, функция распределения.

Законом распределения непрерывной случайной величины Х наз-ется соответствие между каждым ее возможным значением Х₁ и вероятностью ее появление р₁

Функции распределения вероятностей (интергальной функций) непрерывной случной величины Х наз-ется функция F(x) равная при каждом €R вероятности того что Х в результате испытания примет значения меньше х:

Полностью распределения вероятностей прерывной случайной величины Х, называется функция f(x) задаваемая равенством:

15. Нормальное распределение социологических данных, его основные характеристики и причины значительной распространенности в социологии.

Нормальным наз-ется распределения вероятностей таких непрерывных случайных величин у которых плотность распределения вероятностей задается формулой:

где m, - некоторые числа и _>0

Функций распределения вероятностей вычисляется по формуле:

, где 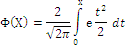- функция Лапласа

Числовые характеристики:

Вероятность того, что случайной величины Х примет значение из интервала (а; b), вычисляется по ф-ле:

16. Равномерный (линейный) закон распределения, его основные статистические характеристики

Непрерывная случайная величина Х принимающая всех свои возможные значение только на отрезке [a,b] наз-ется равномерно распределенной, если ее плотность паспределения равна:

,

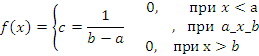Функций распределения F(x) описывается формулой:

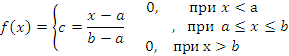
Числовые характеристики:

Вероятность попадания случайной величины Х в интервал (а₁; а₂), где (а₁; а₂) (а; b), вычисляется по ф-ле:

17. Показательный закон распределения.

Непрерывная случайная величин Х наз-ется экспоненциально распределенной, если ее плотность распределения равна:

- положительный параметр.

Интергальная функция F(x) имеет вид:

Числовые характеристики:

Вероятность попадания случайной величины Х в интервал (а; b), вычисляется по ф-ле:

18. Закон распределения Пуассона.

По закону распределения Пуассона. Если число п очень велико, р очень мало и вероятность P(X = k) появления события А ровно К раз вычисляется по ф-ле Пуассона:

, где =пр

19. Математическое ожидание непрерывной случайной величины: определения, свойства, формулы для вычисления.

Математическое ожидание М(х) непрерывной случайной величины Х наз-ется число, вычисляемое по ф-ле:

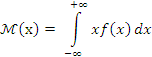
при условии, что этот несобственный интеграл первого рода сходится.

Св-ва математического ожидания:

1. М(С)=С, где С – постоянная величина;

2. М(СХ)=С*М(Х), где С – постоянная величина;

3. М(Х₁+Х₂)=М(Х₁)+М(Х₂).

20. Дисперсия дискретной непрерывной величины: определения, свойства, формулы для вычисления.

Дисперсией D(X) непрерывной случайной величине Х наз-ется математическое ожидание квадрата отклонения случайной величины Х, от ее математического ожидания.

Св-ва дисперсии:

1. D(X)D(C)=0, где С - постоянная величина;

2. D(СХ)=С*D(Х), где С – постоянная величина;

3. D(Х₁+Х₂)=D(Х₁)+D(Х₂)

4. Дисперсия вычисления по ф-ле

21. Среднее квадратическое отклонение непрерывной случайной

величины: определения, свойства, формулы для вычисления.

Среднее квадратическое отклонение непрерывной случайной величины Х наз-ют квадратный корень из ее дисперсии:

Св-ва дисперсии:

5. D(X)D(C)=0, где С - постоянная величина;

6. D(СХ)=С*D(Х), где С – постоянная величина;

7. D(Х₁+Х₂)=D(Х₁)+D(Х₂)

8. Дисперсия вычисления по ф-ле:

22. Специфика и проблемы использования математики для решения социологических задач. (235 во

23. Числовые и геометрические характеристики статистического ряда распределения. 236

24. Статистическая гипотеза, критерий, уровень значимости - определение понятий.

№1. Статистической гипотез наз-ется предположение о виде распределения, о параметрах известных распределений.

№2. Выдвинутая гипотеза наз-ется нулевой (или основной) и обозначается Но.

Гипотеза, которая противоречит нулевой, наз-ется конкурирующей гипотезой и обозначается Н_1.

№3. Гипотеза наз-ется простой, если она содержит только одно предложение.

Гипотеза наз-ется сложной, если она состоит из конечного или бесконечного числа предположений.

№4. Сопоставление выдвинутой гипотезы с экспериментальными данными наз-ется проверкой гипотезы.

№5. Правосторонней критической областью для проверки 0-ой гипотезы с уровнем значимости а наз-етс совокупность значений критерия проверки Z, для которых выполняется равенство: Р(Z>Zкрит.)=а, где Zкрит. – некоторое число, наз-мое границией критической области.

Левосторонней критической областью для проверки 0-ой гипотезы с уровнем значимости а наз-етс совокупность значений критерия проверки Z, для которых выполняется равенство: Р(Z<-Zкрит.)=а, где Zкрит. – некоторое число, наз-мое границией критической области.

Двусторонней критической областью для проверки 0-ой гипотезы с уровнем значимости а наз-етс совокупность значений критерия проверки Z, для которых выполняется равенство:

Р(Z_{2 крит.} < Z< Z_1крит.)=а, где Z 1крит. Z 2крит – некоторое число, наз-мое границией критической области.