
§ 6. Деление отрезка в данном отношении
Говорят,
что точка
![]() делит отрезок
делит отрезок
![]() в отношении
в отношении
![]() ,
если
,
если
![]() ,
или
,
или
![]() (рис. 13).
(рис. 13).
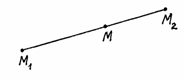
Рис. 13
Пусть
координаты точек
![]() и
и
![]() известны:
известны:
![]() ,
,
![]() .
Найдем координаты точки
.
Найдем координаты точки
![]() .
Очевидно, что
.
Очевидно, что
![]() ,
где
,
где
![]() ,
,
![]() .
Приравнивая координаты векторов, найдем:
.
Приравнивая координаты векторов, найдем:
![]() ,
,
![]() ,
,
![]() . (2.6)
. (2.6)
В
частности, если
–
середина отрезка
,
то
![]() ,
тогда
,
тогда
![]() ,
,
![]() ,
,
![]() . (2.7)
. (2.7)
Пример
4.
Даны вершины треугольника
![]() ,
,
![]() ,
,
![]() .
Найти точку пересечения медиан этого
треугольника и орт вектора
.
Найти точку пересечения медиан этого
треугольника и орт вектора
![]() (рис. 14).
(рис. 14).
Решение.
AD
– медиана, следовательно, D
– середина
отрезка BC,
ее координаты находятся по формулам
(2.7):
![]() ,
,
![]() ,
,
![]() ,
то есть
,
то есть
![]() .
Медианы точкой пересечения K
делятся в отношении 2:1, значит,
.
Медианы точкой пересечения K
делятся в отношении 2:1, значит,
![]() ,
тогда по формулам (2.6) найдем координаты
точки K:
,
тогда по формулам (2.6) найдем координаты
точки K:
![]() ,
,
![]() ,
,
![]() .
Таким образом, точка пересечения медиан
–
.
Таким образом, точка пересечения медиан
–
![]() .
Найдем координаты вектора
по формуле (2.3) и его длину по формуле
(2.2):
.
Найдем координаты вектора
по формуле (2.3) и его длину по формуле
(2.2):
![]() ;
;
![]() .
Координаты единичного вектора совпадают
с его направляющими косинусами. По
формулам (2.5)
.
Координаты единичного вектора совпадают
с его направляющими косинусами. По
формулам (2.5)
![]() ,
,
![]() ,
,
![]() ,
следовательно,
,
следовательно,
![]() – орт вектора
.
– орт вектора
.
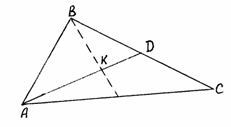
Рис. 14
Пример
5.
Показать, что точки
![]() ,
,
![]() ,
,
![]() лежат на одной прямой, причем A
– между B
и C.
лежат на одной прямой, причем A
– между B
и C.
Решение.
Рассмотрим векторы
![]() и
и
![]() (рис.
15). Если точки A,
B, C
лежат на одной прямой, то векторы
и
должны
быть кол-линеарны (условие 2.4). А если
точка A
лежит между B
и C,
то
и
должны
быть сонаправлены (коэффициент
пропорциональности координат
(рис.
15). Если точки A,
B, C
лежат на одной прямой, то векторы
и
должны
быть кол-линеарны (условие 2.4). А если
точка A
лежит между B
и C,
то
и
должны
быть сонаправлены (коэффициент
пропорциональности координат
![]() )
и
)
и
![]() .
Проверим выполнение этих условий.
.
Проверим выполнение этих условий.
![]() ,
,
![]() ;
;
![]() ,
следовательно,
,
следовательно,
![]() .
Координаты вектора
больше, значит, он длиннее и точка A
лежит между B
и C.
.
Координаты вектора
больше, значит, он длиннее и точка A
лежит между B
и C.
8) Условие параллельности прямых заключается в равенстве их угловых коэффициентов.
tgφ1=tgφ2 или k1=k2
Условие перпендикулярности прямых заключается в том, что произведение их угловых коэффициентов равно –1
k1k2=-1
Пример 6. Проверить, выполняется ли условие параллельности прямых 2х-3у+1=0 и 4х-6у-5=0 ?
Решение:
Угловые коэффициенты этих прямых
![]() ,
т.е. условие параллельности выполнено.
,
т.е. условие параллельности выполнено.
Пример 7. Составить уравнение прямой линии, проходящей через точку (1;2) параллельно прямой 2х-3у+1=0.
Решение.
Угловой коэффициент k прямой линии, для
которой нужно составить уравнение,
равен угловому коэффициенту
![]() данной
прямой в силу условия параллельности
этих прямых. Таким образом,
данной
прямой в силу условия параллельности
этих прямых. Таким образом,
![]() получим
искомое уравнение:
получим
искомое уравнение:
![]() или,
умножая на 3: 3y-6=2(x-1), или 3y-6=2x-2, откуда
окончательно находим: 2x-3y+4=0
или,
умножая на 3: 3y-6=2(x-1), или 3y-6=2x-2, откуда
окончательно находим: 2x-3y+4=0
Пример 8. При каком значении k уравнение y=kx+1 определяет прямую, перпендикулярную к прямой у=2х-1?
Решение:
Угловой коэффициент второй прямой k2=2.
Условие перпендикулярности дает 2k=-1,
откуда
![]()
Пример 9. Составить уравнение прямой линии, проходящей через точку (-1;1) перпендикулярно к прямой 3х-у+2=0.
Решение:
Искомый угловой коэффициент обозначим
через k1,
угловой коэффициент данной прямой k2,
как видно из ее уравнения, равен 3. Условие
перпендикулярности k1k2=-1
нам дает: 3k1=-1,
откуда
![]() .
Таким образом, искомое уравнение
.
Таким образом, искомое уравнение
![]() ,
или 3у-3=-х-1, и окончательно x+3y-2=
,
или 3у-3=-х-1, и окончательно x+3y-2=
9) Определение 9.15.
Ненулевой вектор называется направляющим вектором прямой a, если он лежит либо на прямой a, либо на прямой, параллельной a.
Определение 9.16.
Углом
между ненулевыми векторами называется
угол между прямыми, для которых данные
вектора являются направляющими. Угол
между любым вектором и нулевым вектором
по определению считаем равным нулю.
Если угол между векторами равен 90°, то
такие вектора называются перпендикулярными.
Угол между векторами будем обозначать
так:
![]()
Определение 9.17.
Скалярным
произведением векторов
![]() и
и
![]() называется
произведение их длин на косинус угла
между ними:
называется
произведение их длин на косинус угла
между ними:
|
Совершенно аналогично, как в планиметрии, доказываются следующие утверждения:
Скалярное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.
Скалярный квадрат вектора, то есть скалярное произведение его самого на себя, равно квадрату его длины.
Скалярное произведение двух векторов
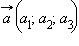 и
и
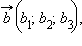 заданных
своими координатами, может быть вычислено
по формуле
заданных
своими координатами, может быть вычислено
по формуле
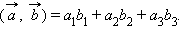
Перечислим основные свойства скалярного произведения, которые также доказываются аналогично планиметрическим.
Для
любых векторов
![]()
![]() и
и
![]() и
любого числа λ справедливы равенства:
и
любого числа λ справедливы равенства:
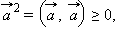 причем
причем

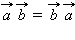 (переместительный
закон).
(переместительный
закон).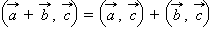 (распределительный
закон).
(распределительный
закон).
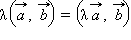 (сочетательный
закон).
(сочетательный
закон).
