
- •Матрицы и линейные операции над ними.
- •Сложение матриц
- •Умножение матрицы на число
- •Определение умножения матриц и свойства операции умножения.
- •Свойства произведения матриц
- •3. Степени квадратной матрицы
- •4.Транспонирование матриц
- •10.Основные свойства определителей
- •12.Обратная матрица
- •Свойства обратных матриц
- •14.Правило Крамера решения систем линейных уравнений
- •15.Ранг матрицы
- •Свойства ранга матрицы
- •16.Теорема о базисном миноре
- •18.Критерий совместности системы линейных уравнений
- •19.Однородные системы линейных уравнений
- •Свойства решений однородной системы линейных уравнений
- •22.Определение линейного пространства и простейшие следствия из аксиом.
- •3*. Существование нейтрального элемента).
- •Простейшие следствия из аксиом.
- •23.Определение линейной зависимости и независимости элементов линейного пространства. Свойства линейной зависимости и независимости.
- •Простейшие свойства линейной зависимости
- •24.Базис и координаты в линейном пространстве. Свойства координат векторов.
- •Свойства координат векторов
- •25.Матричный критерий линейной зависимости и независимости.
- •26.Определение размерности линейного пространства. Теорема о связи базиса и размерности. Следствия.
- •7. Как пример аффинного, евклидова и метрического пространств.
- •35.Определение матрицы перехода и её свойства.
- •Свойства матрицы перехода
- •38. Определение линейного оператора и его простейшие свойства.
- •39. Определение матрицы линейного оператора.
- •42.Операции над линейными операторами
- •50.Определение и свойства собственных векторов.
- •Свойства собственных векторов
- •§ 13. Правило нахождения собственных векторов
- •Правило нахождения присоединенных векторов
- •54. Определение приводимости квадратной матрицы к диагональному виду и вторая теорема о приводимости. Следствие.
- •60.Канонический вид квадратичной формы
- •61.Знакоопределенные квадратичные формы
- •62.Критерий Сильвестра знакоопределенности квадратичных форм
- •63.Действительные евклидовы пространства
- •Простейшие следствия из аксиом
- •64.Комплексные евклидовы (унитарные) пространства
- •65. Неравенство Коши – Буняковского.
- •68.Выражение скалярного произведения через координаты перемножаемых векторов
- •82.Ортогональные операторы в трехмерном евклидовом пространстве
- •83.Симметричные операторы в
- •84.Общее определение тензора
- •90.Основные определения и примеры
- •Примеры
- •Простейшие следствия из аксиом
68.Выражение скалярного произведения через координаты перемножаемых векторов
Определение. Матрицей Грама системы векторов
 (6.9)
(6.9)
евклидова
пространства
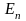 называется матрица
называется матрица
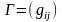 ,
где
,
где
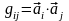 .
.
Нетрудно
показать, что в случае действительного
пространства матрица Г симметричная и
все ее главные миноры положительны.
Если же пространство комплексное, то
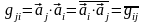 ,
т. е.
,
т. е.
Выберем в какой-либо базис
(6.11)
и
обозначим
его матрицу Грама. Выберем также
произвольные векторы
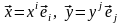 пространства
.
Тогда
пространства
.
Тогда
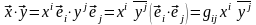 –
–
координатная форма записи скалярного произведения в комплексном евклидовом пространстве;
 –
–
координатная
форма записи скалярного произведения
в действительном
пространстве. Так как
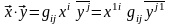 ,
то
,
то
 –
–
матричная
форма записи скалярного произведения
в комплексном пространстве;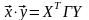 –
–
в
действительном пространстве. В
ортонормированном базисе скалярное
произведение вычисляется так: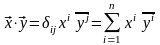 –
–
координатная
форма записи скалярного произведения
в комплексном евклидовом пространстве;
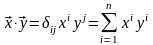 –
–
в
действительном пространстве;
 –
(6.12)
–
(6.12)
матричная форма записи скалярного произведения в комплексном пространстве;
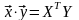 –
–
в действительном пространстве.
73-74.Самосопряженные линейные операторы
Определение.
Линейный оператор
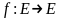 называется самосопряженным,
если он сопряжен самому себе (
называется самосопряженным,
если он сопряжен самому себе (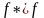 ),
т. е., если
),
т. е., если
 :
:
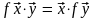 .
(7.4)
.
(7.4)
В комплексных евклидовых пространствах самосопряженные линейные операторы называются эрмитовыми, а в действительных – симметричными.
Теорема 7.3. Для того чтобы линейный оператор комплексного евклидова пространства в себя был эрмитовым, необходимо и достаточно, чтобы его матрица в некотором, а значит, и в любом ортонормированном базисе пространства была эрмитовой.
Для того чтобы линейный оператор действительного евклидова пространства в себя был симметричным, необходимо и достаточно, чтобы его матрица в некотором, а значит, и в любом ортонормированном базисе пространства была симметричной.
Теорема 7.4. Все собственные значения эрмитова оператора действительны.
Следствия. 1. Все характеристические числа эрмитовой матрицы действительны.
2. Все характеристические числа симметричной матрицы действительны.
3. Любой симметричный оператор имеет, по крайней мере, одно собственное значение.
Теорема 7.5. Собственные векторы самосопряженного линейного оператора с различными собственными значениями взаимно ортогональны.
Теорема
7.6. Для любого
самосопряжённого оператора
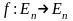 в пространстве
существует ортонормированный базис,
состоящий из собственных векторов
оператора
.
в пространстве
существует ортонормированный базис,
состоящий из собственных векторов
оператора
.
77-79.Изометрии
Определение. Линейный оператор f евклидова пространства Е в себя называется изометрией, если он сохраняет скалярное произведение, т. е. если
 (7.18)
(7.18)
Изометрии в комплексном евклидовом пространстве называются унитарными операторами, а в действительном – ортогональными.
Теорема 7.10. Если – собственное значение изометрии, то ||=1.
Замечание. Собственные значения ортогонального оператора равны 1 или –1. Ортогональный оператор в пространстве четной размерности может и не иметь собственных значений, но в пространстве нечетной размерности имеет хотя бы одно.
Теорема 7.11. Для того чтобы линейный оператор был изометрией, необходимо и достаточно, чтобы он сохранял длины векторов.
Теорема 7.12. Изометрия любой ортонормированный базис пространства переводит в ортонормированный базис. Обратно, если линейный оператор некоторый ортонормированный базис пространства переводит в ортонормированный базис, то f – изометрия.
81.Ортогональные операторы на евклидовой плоскости
Выберем
на евклидовой плоскости
 какой-либо ортонормированный базис
какой-либо ортонормированный базис
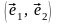 .
Если А
– матрица ортогонального оператора
.
Если А
– матрица ортогонального оператора
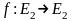 в этом базисе, то она ортогональна.
Значит,
в этом базисе, то она ортогональна.
Значит,
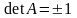 .
Найдем характеристический многочлен
матрицы А:
.
Найдем характеристический многочлен
матрицы А:
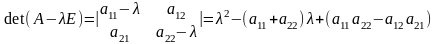 .
.
Рассмотрим сначала
случай, когда
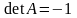 .
Тогда характеристическое уравнение
имеет вид
.
Тогда характеристическое уравнение
имеет вид
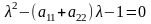 .
Это уравнение имеет два различных
действительных корня. Значит, ортогональный
оператор
имеет два различных собственных значения:
.
Это уравнение имеет два различных
действительных корня. Значит, ортогональный
оператор
имеет два различных собственных значения:
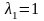 и
и
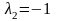 .
В таком случае в
существует ортонормированный базис
.
В таком случае в
существует ортонормированный базис
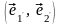 ,
состоящий из собственных векторов
оператора
,
в котором матрица
,
состоящий из собственных векторов
оператора
,
в котором матрица
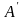 оператора
имеет диагональный вид:
оператора
имеет диагональный вид:
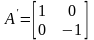 .
.
Линейный
оператор с этой матрицей, как мы знаем,
есть не что иное, как оператор симметрии
относительно оси, направление которой
задается вектором
 .
.
Пусть теперь
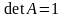 .
Определим в этом случае элементы матрицы
А,
учитывая, что она ортогональная, т. е.
что
.
Определим в этом случае элементы матрицы
А,
учитывая, что она ортогональная, т. е.
что
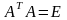 .
Пусть
.
Пусть
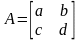 .
.
Тогда
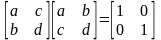 ,
,
откуда получаем систему для определения элементов матрицы:
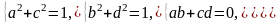 (7.24)
(7.24)
Из
первых двух уравнений системы (7.24) видно,
что можно положить
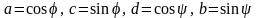 ,
где
и
,
где
и
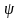 –
некоторые углы, причем
–
некоторые углы, причем
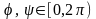 (так как нам важно знать не сами углы, а
значения их синусов и косинусов).
Последние два уравнения этой системы
определяют соотношения между углами
и
:
(так как нам важно знать не сами углы, а
значения их синусов и косинусов).
Последние два уравнения этой системы
определяют соотношения между углами
и
:
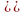 .
.
Значит, матрица А выглядит так:
 .
.
Как
мы уже знаем, это матрица оператора
поворота плоскости на угол
вокруг начала координат. В частности,
если
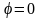 ,
то
,
то
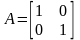 ,
т. е. получаем тождественный оператор.
Если же
,
т. е. получаем тождественный оператор.
Если же
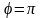 ,
то
,
то
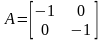 .
Этой матрице соответствует оператор
симметрии относительно начала координат.
.
Этой матрице соответствует оператор
симметрии относительно начала координат.
Таким образом, ортогональные операторы на евклидовой плоскости – это тождественный оператор, симметрия относительно начала координат или относительно некоторой оси, либо поворот плоскости вокруг начала координат.
