
- •Матрицы и линейные операции над ними.
- •Сложение матриц
- •Умножение матрицы на число
- •Определение умножения матриц и свойства операции умножения.
- •Свойства произведения матриц
- •3. Степени квадратной матрицы
- •4.Транспонирование матриц
- •10.Основные свойства определителей
- •12.Обратная матрица
- •Свойства обратных матриц
- •14.Правило Крамера решения систем линейных уравнений
- •15.Ранг матрицы
- •Свойства ранга матрицы
- •16.Теорема о базисном миноре
- •18.Критерий совместности системы линейных уравнений
- •19.Однородные системы линейных уравнений
- •Свойства решений однородной системы линейных уравнений
- •22.Определение линейного пространства и простейшие следствия из аксиом.
- •3*. Существование нейтрального элемента).
- •Простейшие следствия из аксиом.
- •23.Определение линейной зависимости и независимости элементов линейного пространства. Свойства линейной зависимости и независимости.
- •Простейшие свойства линейной зависимости
- •24.Базис и координаты в линейном пространстве. Свойства координат векторов.
- •Свойства координат векторов
- •25.Матричный критерий линейной зависимости и независимости.
- •26.Определение размерности линейного пространства. Теорема о связи базиса и размерности. Следствия.
- •7. Как пример аффинного, евклидова и метрического пространств.
- •35.Определение матрицы перехода и её свойства.
- •Свойства матрицы перехода
- •38. Определение линейного оператора и его простейшие свойства.
- •39. Определение матрицы линейного оператора.
- •42.Операции над линейными операторами
- •50.Определение и свойства собственных векторов.
- •Свойства собственных векторов
- •§ 13. Правило нахождения собственных векторов
- •Правило нахождения присоединенных векторов
- •54. Определение приводимости квадратной матрицы к диагональному виду и вторая теорема о приводимости. Следствие.
- •60.Канонический вид квадратичной формы
- •61.Знакоопределенные квадратичные формы
- •62.Критерий Сильвестра знакоопределенности квадратичных форм
- •63.Действительные евклидовы пространства
- •Простейшие следствия из аксиом
- •64.Комплексные евклидовы (унитарные) пространства
- •65. Неравенство Коши – Буняковского.
- •68.Выражение скалярного произведения через координаты перемножаемых векторов
- •82.Ортогональные операторы в трехмерном евклидовом пространстве
- •83.Симметричные операторы в
- •84.Общее определение тензора
- •90.Основные определения и примеры
- •Примеры
- •Простейшие следствия из аксиом
Матрицы и линейные операции над ними.
Матрицей
размеров
 (читается m
на n)
называется
числовая
таблица,
имеющая m
строк и n
столбцов.
(читается m
на n)
называется
числовая
таблица,
имеющая m
строк и n
столбцов.
Если
m = n,
то матрица
 называется квадратной,
а число n
называется ее порядком.
называется квадратной,
а число n
называется ее порядком.
Квадратная
матрица
 называется верхней треугольной, если
называется верхней треугольной, если
 при
при
 ,
нижней треугольной, если
при
,
нижней треугольной, если
при
 .
Неквадратная матрица
при n > m
называется трапециевидной, если
при i > j.
Например, А
– верхняя треугольная, В
– нижняя
треугольная, С
– трапециевидная
матрицы:
.
Неквадратная матрица
при n > m
называется трапециевидной, если
при i > j.
Например, А
– верхняя треугольная, В
– нижняя
треугольная, С
– трапециевидная
матрицы:
 ;
;

Сложение матриц
Определение.
Суммой
матриц
 и
и
 называется матрица
называется матрица
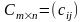 такая что
такая что



 .
.
Очевидно, что сложение произвольных матриц одинаковых размеров обладает следующими свойствами.
1°. A + B = B + A (коммутативность).
2°. (A + B) + C = A + (B + C) (ассоциативность).
3°.
 (существование нейтрального элемента).
(существование нейтрального элемента).
4°.
 (существование противоположного
элемента).
(существование противоположного
элемента).
Умножение матрицы на число
Определение.
Произведением
матрицы
на число
называется матрица
 такая, что
такая, что
 :
:
 .
.
Нетрудно убедиться, что для операции умножения матрицы на число справедливы следующие свойства.
1°. (А + В) = А + В.
2°. ( + ) A = A + A.
3°. () A = (A).
4°. 1A = A.
Здесь А и В – произвольные матрицы одних и тех же размеров, и – произвольные числа
Определение умножения матриц и свойства операции умножения.
Определение.
Произведением матрицы
на матрицу
 называется матрица AB
=
называется матрица AB
=
 такая, что
такая, что
 :
:
 .
.
Свойства произведения матриц
1°. (AB)C = A(BC) – ассоциативность.
Это свойство надо формулировать так: если определены произведения матриц AB и (AB)C, то определены и произведения BC и A(BC), причем (AB)C = A(BC).
2°. A(B + C) = AB + AC – дистрибутивность умножения относительно сложения.
3°. (A) B = A (B) = (AB).
4°. A = A; AE = A.
3. Степени квадратной матрицы
Если
А
– квадратная матрица, то определено
произведение АА,
которое называется квадратом матрицы
А
и обозначается А2
. Квадрат матрицы А
является квадратной матрицей того же
порядка, что и А,
поэтому определено и произведение АА2.
Вообще, если для квадратной матрицы
определена степень
 ,
то по определению
,
то по определению
 .
.
Лемма
1.2. Для любой
квадратной матрицы А
и для любого натурального n
справедливо равенство
 .
.
Если произведение матриц коммутативно, то они называются коммутирующими или перестановочными. Таким образом, степени одной и той же квадратной матрицы перестановочны.
Можно доказать, что натуральные степени квадратной матрицы обладают следующими свойствами:
1°.
 :
: ;
;
2°.
:
 .
.
Если
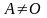 ,
то по определению считается, что A0
= E.
,
то по определению считается, что A0
= E.
4.Транспонирование матриц
Определение.
Матрица
 называется транспонированной
к матрице
,
если
называется транспонированной
к матрице
,
если


 .
.
Таким образом, из определения видим, что при транспонировании матрицы строки становятся столбцами и наоборот. Например, если
 ,
то
,
то
 .
.
Кроме
обозначения AT
для матрицы, транспонированной к А,
используют еще и следующие:
 .
.
Свойства операции транспонирования
1°. .
.
2°. .
.
3°. .
.
4°. .
.
Первые
три свойства практически очевидны.
Докажем четвертое, которое формулируется
так: если определено произведение матриц
АВ,
то определено и произведение
 ,
причем
,
причем
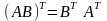 .
.
6-8.Определение определителя квадратной матрицы
Каждой
квадратной матрице поставим в соответствие
число, которое назовем ее определителем
или детерминантом
и будем обозначать
![]() ,
следующим образом:
,
следующим образом:
а)
если
 ,
то
,
то
 (определитель матрицы, состоящей из
одного элемента, равен этому элементу);
(определитель матрицы, состоящей из
одного элемента, равен этому элементу);
б)
если
 ,
то
,
то
 ;
;
в)
если известно, как найти определитель
матрицы
 -го
порядка, то определитель матрицы
-го
порядка, то определитель матрицы
 -го
порядка задается так:
-го
порядка задается так:
 (1.10)
(1.10)
где
 − определитель матрицы
-го
порядка, полученной из исходной
вычеркиванием первой строки и
− определитель матрицы
-го
порядка, полученной из исходной
вычеркиванием первой строки и
 -го
столбца.
-го
столбца.
Определитель квадратной матрицы n-го порядка будем просто называть определителем n-го порядка.
В развернутом виде определитель n-го порядка записывается как таблица, ограниченная с обеих сторон вертикальными чертами (по одной с каждой стороны):

Приведенное выше определение является определением по индукции или определением с помощью разложения по первой строке.
так:
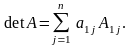
Таким образом, согласно определению, определитель равен сумме произведений элементов первой строки на их алгебраические дополнения.
6-8.Основные леммы об определителях
Лемма 1.3 (о разложении по первому столбцу). Определитель равен сумме произведений элементов 1-го столбца на их алгебраические дополнения, т. е.

Лемма
1.4 (о
равноправии строк и столбцов).
При транспонировании матрицы ее
определитель не меняется, т. е.

Докажите это утверждение самостоятельно, в качестве упражнения, методом математической индукции по размерности определителя.
Лемма 1.5 (о перестановке строк или столбцов). При перестановке в определителе двух строк (столбцов) местами определитель лишь поменяет знак.
Tеорема 1.1 (основная теорема об определителях). Если в определителе выбрать какую-либо строку (столбец), то определитель равен сумме произведений элементов этой строки (столбца) на их алгебраические дополнения, т. е.
 – (1.12)
– (1.12)
разложение по i -й строке,
 –
–
разложение по j-му столбцу.
Следствие. Определитель треугольной или диагональной матрицы равен произведению её диагональных элементов.
