4.2 Решение задачи линейного программирования симплекс-методом

Линейное программирование – область математического программирования, посвященная теории и методам решения экстремальных задач, характеризующихся линейной зависимостью между переменными.

Задача линейного программирования – это задача нахождения значений параметров, обеспечивающих экстремум функции при наличии ограничений на аргументы.

Математическое моделирование – это средство изучения реального объекта, процесса или системы путем их замены математической моделью, более удобной для экспериментального исследования с помощью электронных вычислительных машин. Математические модели в количественной форме, с помощью логико-математических конструкций, описывают основные свойства объекта, процесса или системы, его параметры, внутренние и внешние связи. Математическое моделирование широко применяется в разделе линейного программирования.

Симплекс-метод является основным в линейном программировании. Этот метод является универсальным, применимым к любой задаче линейного программирования в канонической форме. Системой ограничений здесь является система линейных уравнений, в которой количество неизвестных больше количества уравнений.

Если первое найденное базисное решение окажется недопустимым, то с помощью симплексного метода осуществляется переход к другим базисным решениям, которые приближают нас к области допустимых решений, пока на каком-то шаге решения, либо базисное решение окажется допустимым и к нему применяют алгоритм симплексного метода, либо мы убеждаемся в противоречивости системы ограничений.

Таким образом, применение симплекс-метода распадается на два этапа: нахождение допустимого базисного решения системы ограничений или установление факта ее несовместности; нахождение оптимального решения.

Вычисления по симплекс-методу организуются в виде симплекс-таблиц, которые являются сокращенной записью задачи линейного программирования в канонической форме. Перед составлением симплекс-таблицы задача должна быть преобразована, система ограничений приведена к допустимому базисному виду. Для составления симплекс-таблицы во всех равенствах в условии задачи члены, содержащие переменные, переносятся в левую часть, свободные оставляются справа, т.е. задача записывается в виде системы равенств. Далее эта система оформляется в виде симплекс-таблиц.

Алгоритм решения сводится к следующему :

- приведение системы ограничений к каноническому виду путём введения дополнительных переменных для приведения неравенств к равенствам;

- если в исходной системе ограничений присутствовали знаки “ равно ” или “ больше либо равно ”, то в указанные ограничения добавляются;

- искусственные переменные, которые так же вводятся и в целевую функцию со знаками, определяемыми типом оптимума;

- формируется симплекс-таблица;

- рассчитываются симплекс-разности;

- принимается решение об окончании либо продолжении счёта;

- при необходимости выполняются итерации.

На каждой итерации определяется вектор, вводимый в базис, и вектор, выводимый из базиса.

Оптимизационные модели широко используются в экономике и технике. Среди них задачи подбора сбалансированного рациона питания, оптимизации ассортимента продукции, транспортная задача и другие.

Модели всех задач на оптимизацию состоят из следующих элементов:

- целевая функция – величина, которая зависит от переменных и является целью, ключевым показателем эффективности или оптимальности модели;

- переменные – неизвестные величины, которые нужно найти при решении задачи;

- ограничения – условия, которым должны удовлетворять переменные.

Рассмотрим задачи, решаемые симплекс-методом.

Задача № 5.1.21. Исходные данные задачи представлены в формуле 1.

Z =-3*x₁+ 2*x2+x3+ 4*x4-x5-3*x6→ max;

–x4+ 4*x5+ x6 = 6,

x2+x3–2*x4+3*x5 =8, (1)

x1+3*x4–2*x5=3,

x_j >=0, j = 1..6.

Функция на минимизацию представлена в формуле 2.

3*x₁- 2*x2-x3- 4*x4+x5+3*x6 =0; (2)

x6=6+x4+4*x5;

x2=8-x3+2*x4-3*x5;

x1=3-x1-3*x4+2*x5.

Базисными переменными являются х6, х2, и х1, так как их можно выразить из данных уравнений в каноническом виде.

Результаты решения представлены в таблицах 3 – 6

Таблица 3 – Первая симплекс таблица

БП	СЧ	х1	х2	х3	х4	х5	x6
x6	6	0	0	0	-1	4	1
x2	8	0	1	1	-2	3	0
x1	3	1	0	0	3	-2	0
z	0	3	-2	-1	-4	1	3

Таблица 4 – Вторая симплекс таблица

БП	СЧ	х1	х2	х3	х4	х5	x6
x5	7	0,33	0	0	0	3,33	1
x2	10	0,66	1	1	0	1,66	0
x4	1	0,33	0	0	1	-0,66	0
z	4	4,33	-2	-1	0	-1,66	3

Таблица5 – Третья симплекс таблица

БП	СЧ	х1	х2	х3	х4	х5	x6
x5	2,1	0,1	0	0	0	1	0,3
x2	6,5	0,5	1	1	0	0	-0,5
x4	2,4	0,4	0	0	1	0	0,2
z	7,5	4,5	-2	-1	0	0	3,5

Таблица 6 – Итоговая симплекс таблица

БП	СЧ	х1	х2	х3	х4	х5	x6
x5	2,1	0,1	0	0	0	1	0,3
x2	6,5	0,5	1	1	0	0	-0,5
x4	2,4	0,4	0	0	1	0	0,2
z	20,5	5,5	0	1	0	0	2,5

Результат решения в задаче № 5.1.21 равен 20,5 при х1=0, х2=6,5, х3=0, x4=2,4, x5=2,1, x6=0.

На рисунке 4.5 представлено решение задачи с помощью «поиска решений».

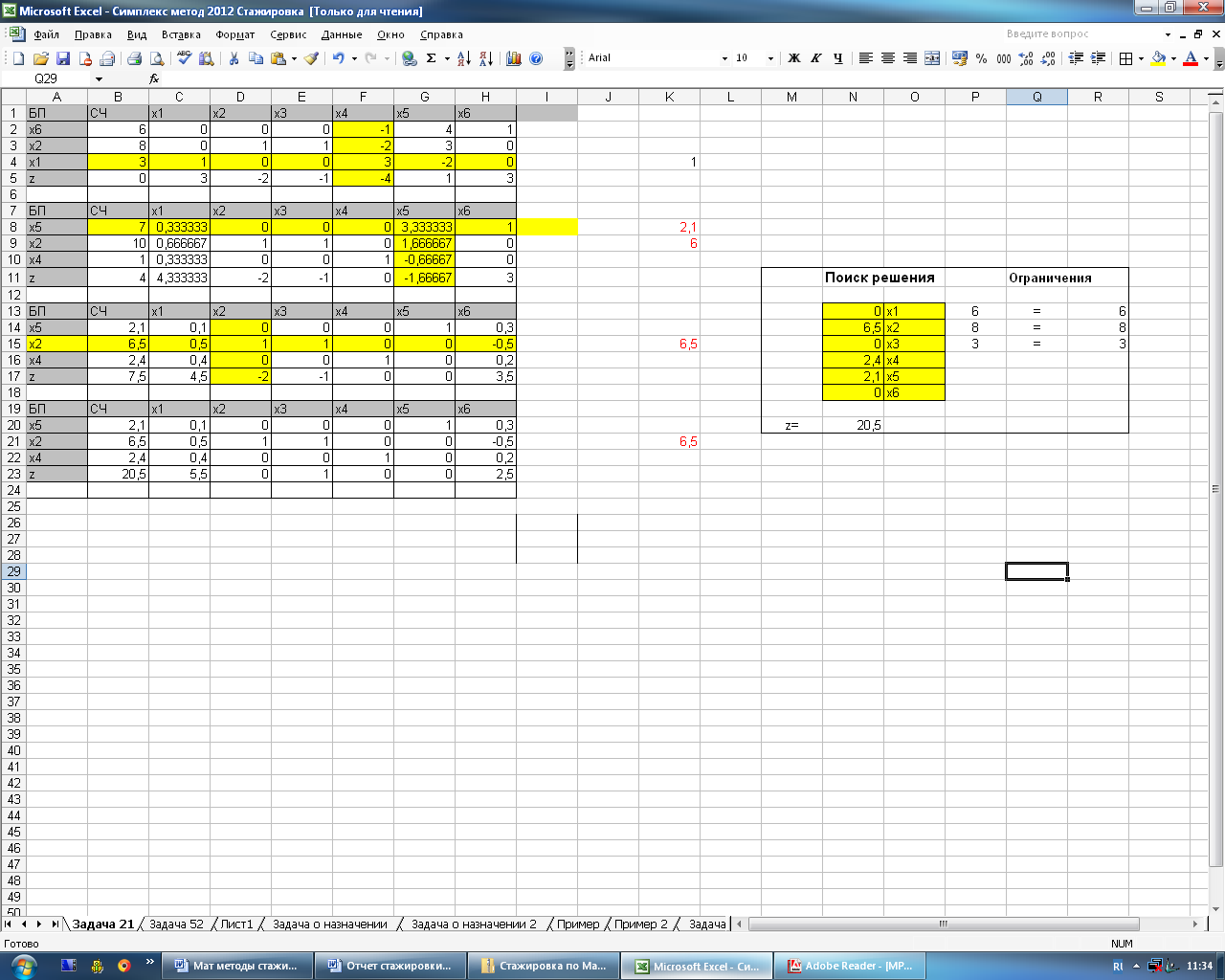
Рисунок 4.5 – Решение задачи с помощью «поиска решений»

На рисунке 4.6 представлена назначение целевой функции и условных ограничений.

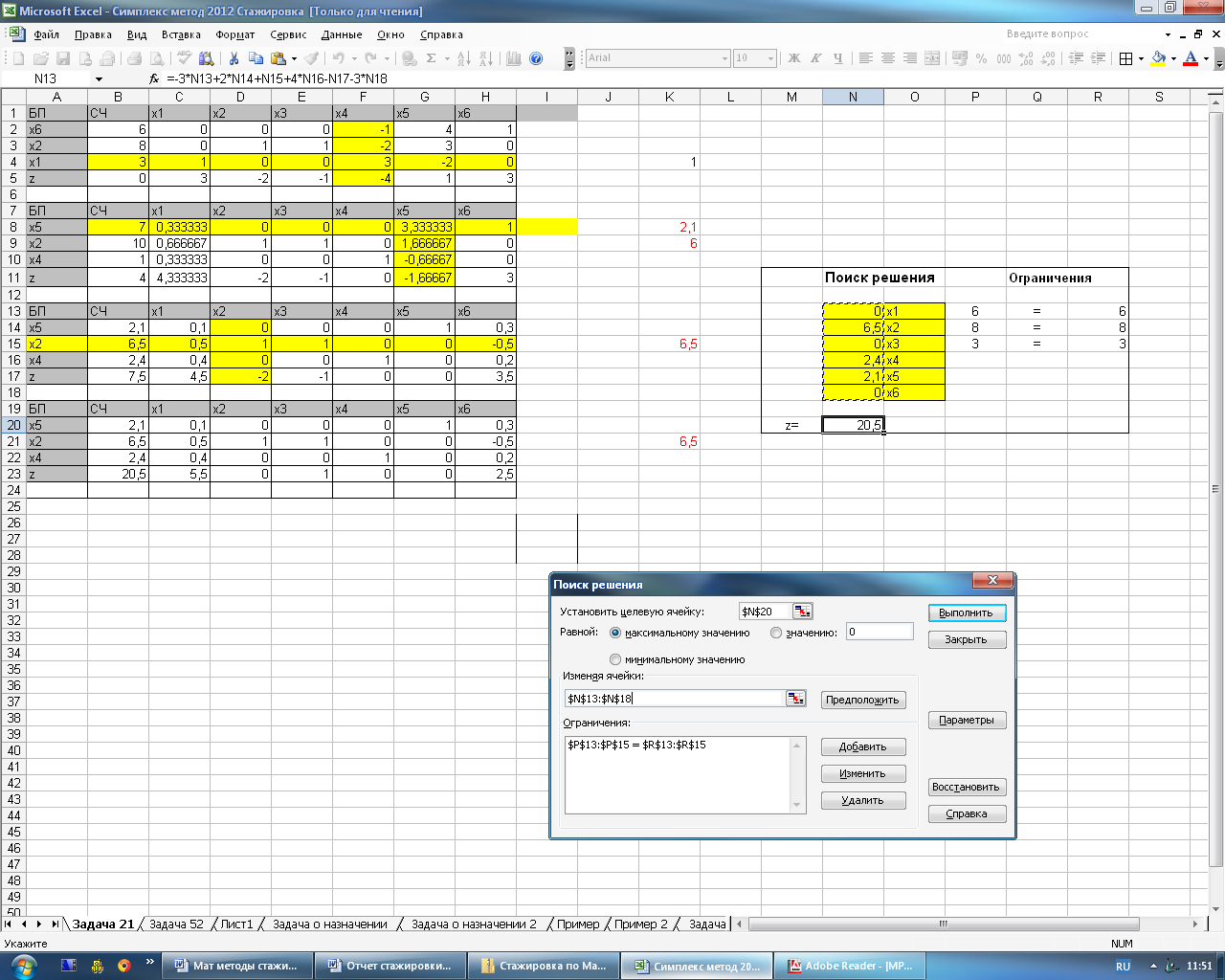
Рисунок 4.6 – Назначение целевой функции и условных ограничений

Задача № 5.1.52. Исходные данные задачи представлены в формуле 2.

Z =-x₁ -4*x₄ -2*x₅ → min;

-2*х₂ +x₃ + 3*x₄ = 4, (3)

x₁+3*x₂ -3*x₄ = 6,

x₂- 4*x₄ + x₅ = 5,

x_j >=0, j = 1..5.

Так как задача на минимизацию то её можно решить аналогичным способом на максимизацию.

В качестве базисных переменных необходимо взять х1, х3, x5 так как их можно выразить из уравнений через переменные x1,x2 и x5.

x1=4+2*x2-x3-3*x4;

x3=6-x1-3*x2+3*x4; (4)

x5=5-x2+4*x4-x5;

Результаты решения представлены в таблицах 7 – 10.

Таблица 7 – Первая симплекс таблица

БП	СЧ	х1	х2	х3	х4	х5
x1	4	0	-2	1	3	0
x3	6	1	3	0	-3	0
x5	5	0	1	0	-4	1
z	0	-1	0	0	-4	-2

Таблица 8 – Вторая симплекс таблица

БП	СЧ	х1	х2	х3	х4	х5
x4	1,33	0	-0,67	0,33	1	0
x3	10	1	1	1	0	0
x5	10,33	0	-1,67	1,33	0	1
z	5,33	-1	-2,67	1,33	0	-2

Таблица 9 – Третья симплекс таблица

БП	СЧ	х1	х2	х3	х4	х5
x4	8	0,67	0	1	1	0
x2	10	1	1	1	0	0
x5	27	1,67	0	3	0	1
z	32	1,67	0	4	0	-2

Таблица 10 – Итоговая симплекс таблица

БП	СЧ	х1	х2	х3	х4	х5
x4	8	0,666667	0	1	1	0
x2	10	1	1	1	0	0
x5	27	1,666667	0	3	0	1
z	86	5	0	10	0	0

Так как индексная строка не содержит отрицательных элементов то Zmax = 86, тогда Zmin = -86, отсюда следует что Zmax=-Zmax.

Результат решения в задаче № 5.1.52 равен -86 при х1=0, х2=10, х3=0, x4=8, x5=27.

На рисунке 4.7 представлено решение задачи с помощью надстройки «поиска решений».

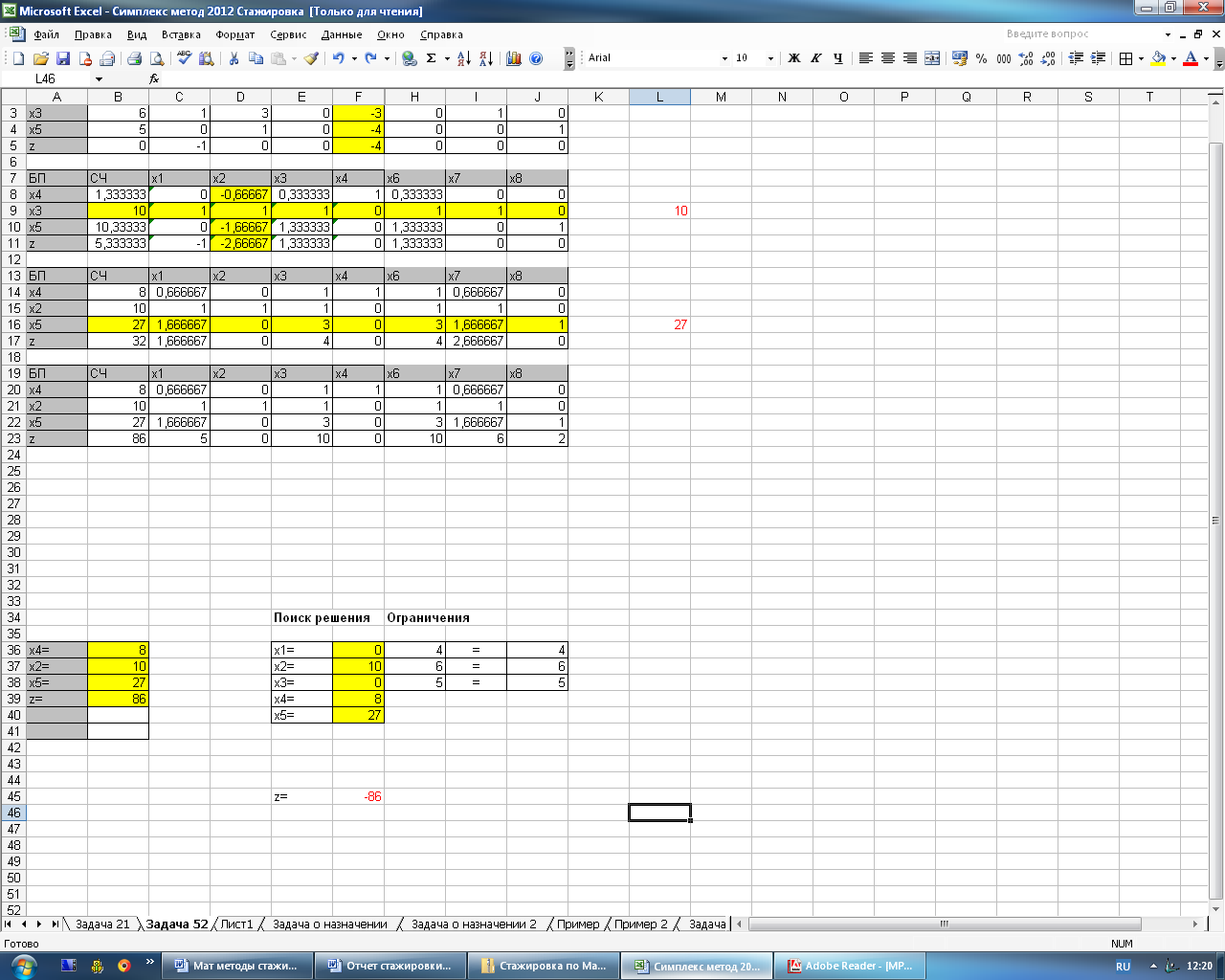
Рисунок 4.7 – Решение задачи с помощью «Поиска решений»

На рисунке 4.8 представлена назначение целевой функции и задание ограничений.

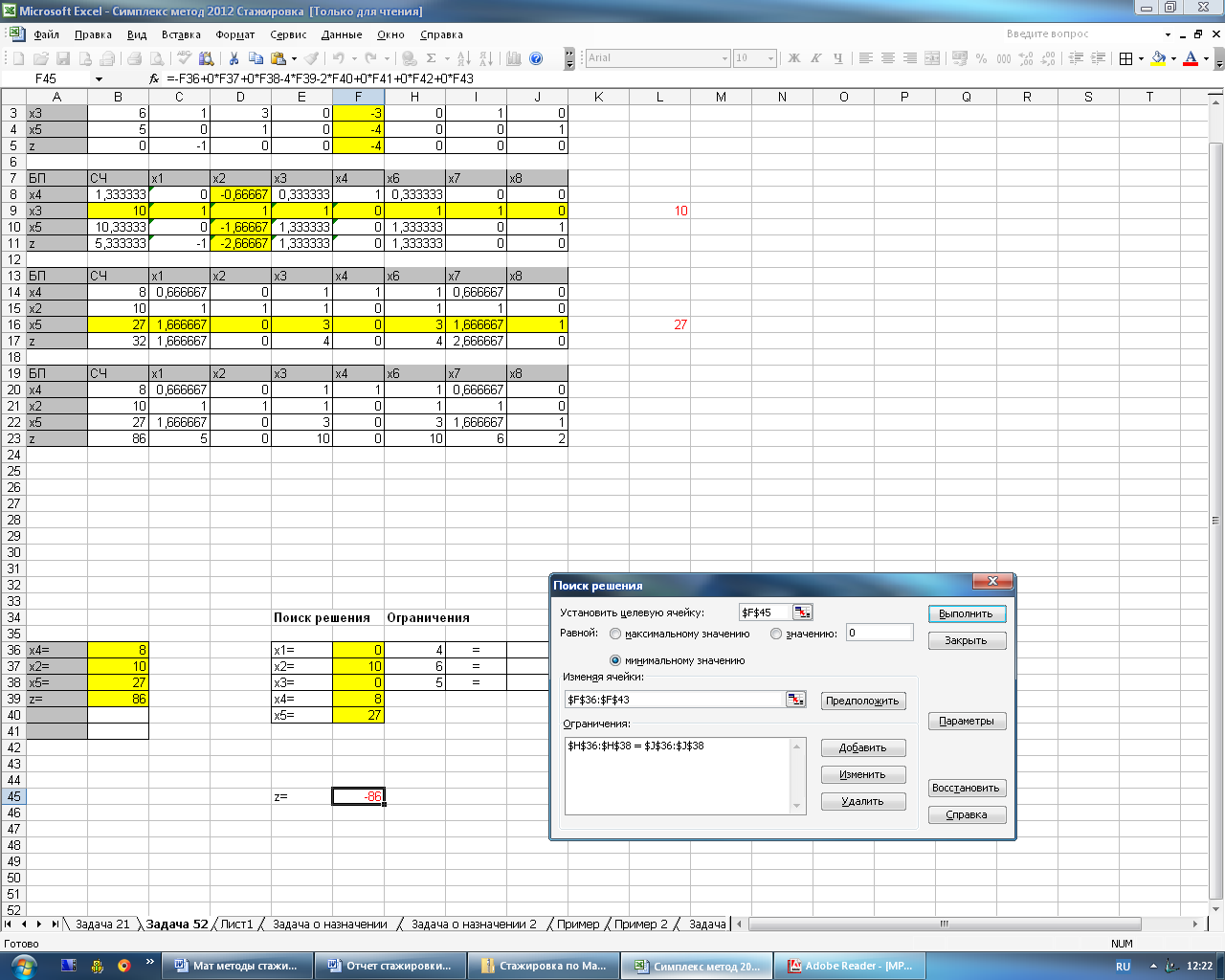
Рисунок 4.8 – Назначение целевой функции и ограничений

Рассмотрим решение данных задач с помощью математического пакета Maple.

В самом общем смысле математический пакет Maple - это среда для выполнения математических расчетов на компьютере, который представляет собой один из наиболее мощных математических пакетов. Решение задач с помощью математического пакета Maple, представлены на рисунках 4.9-4.10.

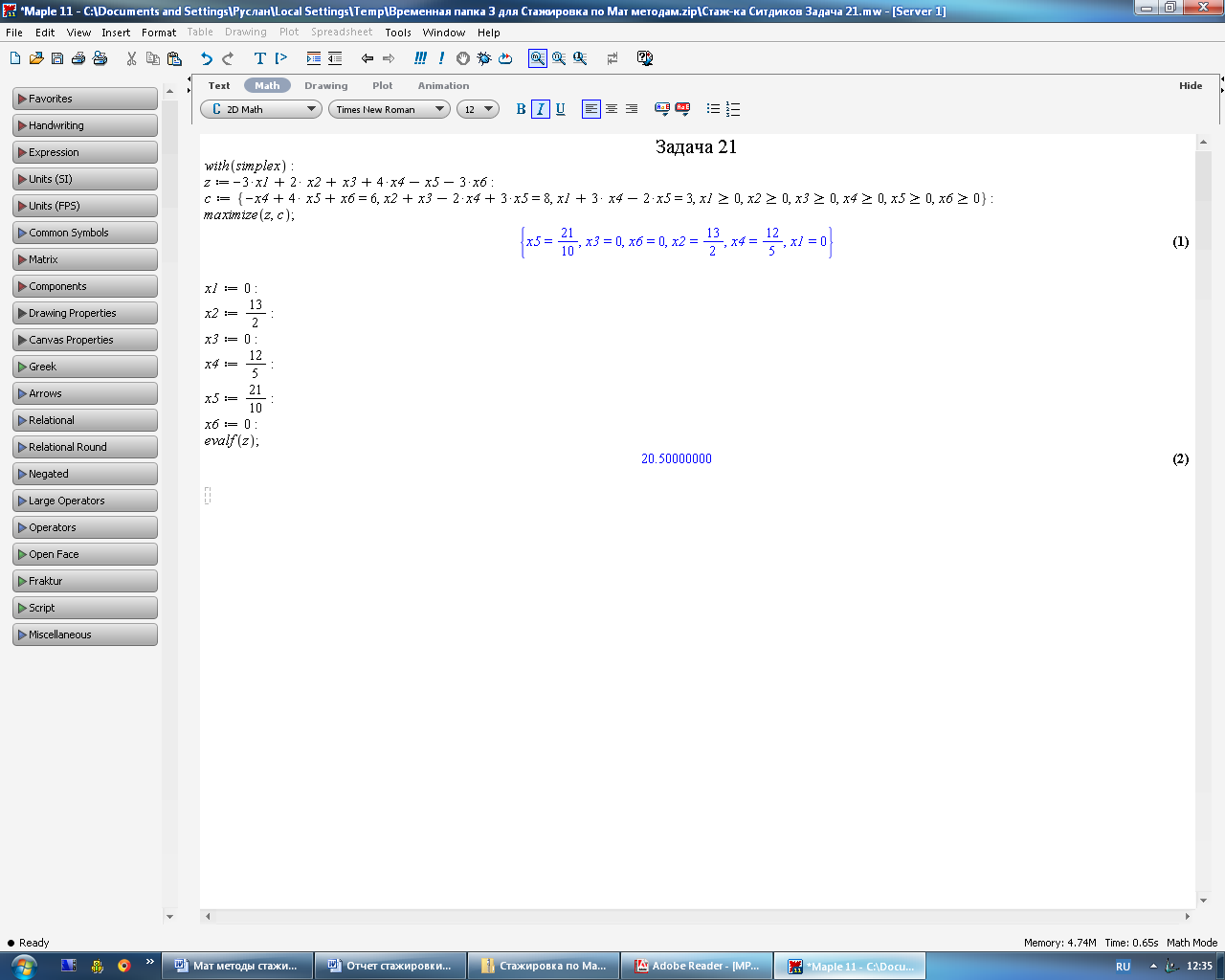
Рисунок 4.9 – Решение задачи №21 c помощью математического пакета Maple

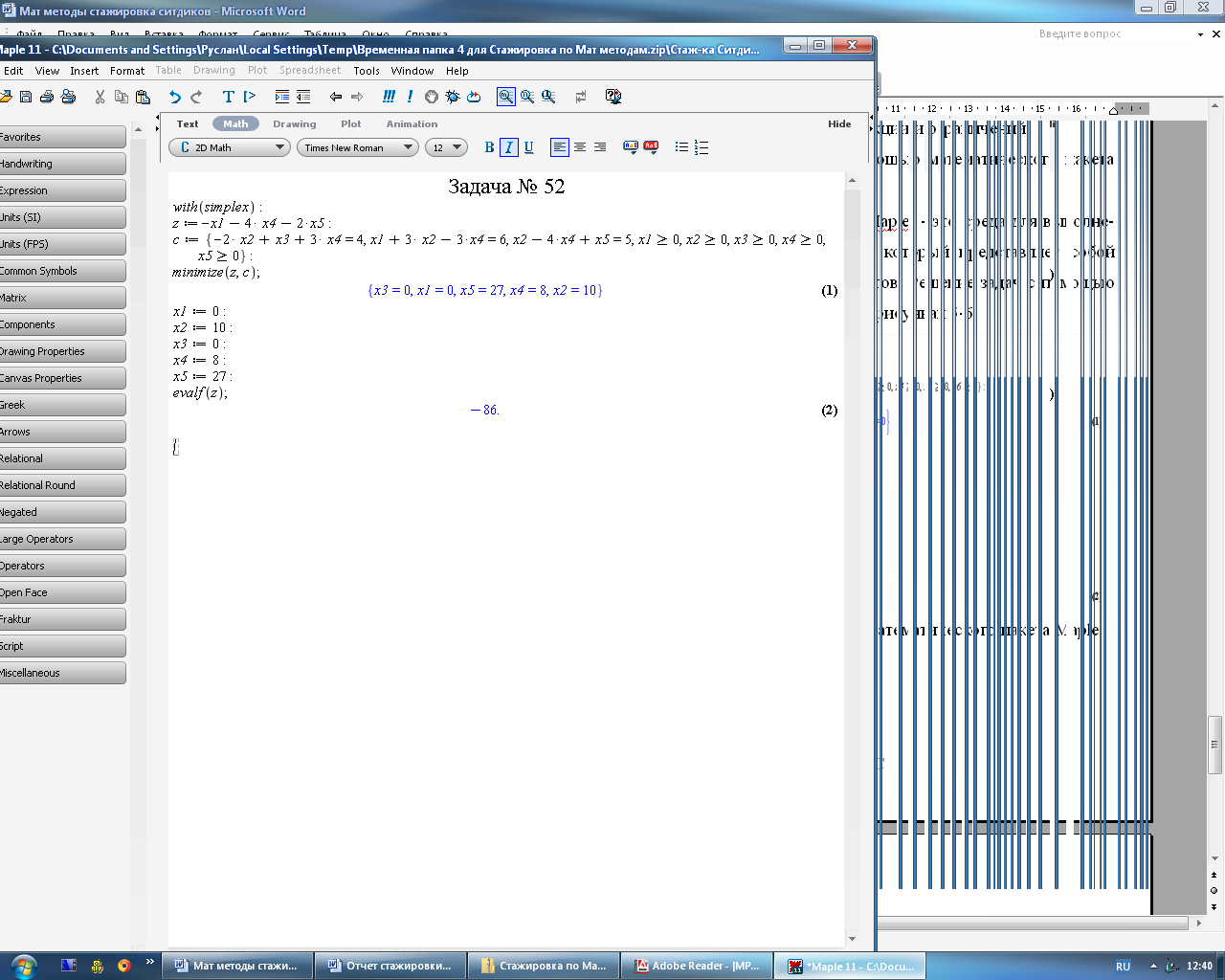
Рисунок 4.10 – Решение задачи №52 c помощью математического пакета Maple

Итак, результаты вычислений в обеих задачах разными способами сошлись. Результат решения в задаче 1 равен 20,5 при х1=0, х2=13/2, х3=0, x4=12/5, х5=21/10, х6=0. Результат решения в задаче 2 равен -86 при х1=0, х2=10, х3=0, x4=8, х5=27.

4.3 Решение транспортной задачи

Одним из главных методов линейного программирования является транспортная задача.

Транспортная задача – математическая задача линейного программирования специального вида об оптимальном плане перевозок грузов из пунктов отправления в пункты потребления, с минимальными затратами на перевозки.

Формулировка транспортной задачи. Пусть некоторый груз находится у m поставщиков в объёмах а1, а2, …, аm и его необходимо доставить n потребителям в объёмах b1, b2, …, bn. Известны cij - стоимости перевозки единицы груза от каждого i-го поставщика каждому j–му потребителю (i = 1, 2, …, m; j = 1, 2, …, n). Требуется составить такой план перевозок, при котором запасы всех поставщиков вывозятся полностью, запросы всех потребителей удовлетворяются полностью, при этом суммарные затраты на перевозку всех грузов минимальны

Исходные данные транспортной задачи записываются в таблице. Неизвестные транспортной задачи являются x_i,j - объёмы перевозок от каждого i-го поставщика каждому j–му потребителю. Исходные данные могут быть также представлены в виде вектора запаса поставщиков А = (а_1, а_{2, ... ,} а_m ), и вектора запросов потребителей В = (в_1, в_{2, ... ,} в_m ), и матрицы стоимостей.

В транспортных задачах под поставщиками и потребителями понимаются различные промышленные и сельскохозяйственные предприятия, заводы, фабрики, склады, магазины и т.д. Под стоимостью перевозок понимают тарифы, расстояния, время, расход топлива и т.п.

Метод решения транспортной задачи основан на нахождении начального опорного решения, а затем улучшения его до получения оптимального решения. К методам нахождения опорного решения транспортная задача линейного программирования относят метод минимальной стоимости, метод северо-западного угла.

Далее необходимо рассмотреть некоторые методы решения транспортных задач.

Рассмотрим метод северо-западного угла.

Существует ряд методов построения начального опорного решения, наиболее простым из которых является метод северо-западного угла.

При этом методе на каждом шаге построения первого опорного плана левая верхняя клетка (северо-западный угол) оставшейся части таблицы. При таком методе заполнение таблице начинается с клетки неизвестного и заканчивается в клетке неизвестного, то есть идёт по диагонали таблицы перевозок.

Заполнение таблицы начинается с её северо-западного угла, допустим, что первая база может полностью удовлетворить потребность первого заказчика. В первую клетку вписываем число равное потребности первого заказчика и исключаем из рассмотрения первый столбец. Далее находим северо-западный угол, уже не учитывая первый столбец. Сравниваем остаток первый базы с потребностями второго заказчика, если удовлетворяет, то пишем число равное потребности второго заказчика, а если нет, то берём в рассмотрение вторую базу. Если сумма остатка первой и второй баз удовлетворяет потребностям второго заказчика, то пишем в клетку число равное потребности второго заказчика и исключаем из рассмотрения первую строку . Тем же способом находим остальные базисные переменные.

Рассмотрим метод минимальной стоимости.

Метод минимальной стоимости прост и позволяет построить опорное решение, достаточно близкое к оптимальному, так как использует матрицу стоимостей транспортной задачи C=(cij).

Как и метод северо-западного угла, он состоит из ряда однотипных шагов, на каждом из которых заполняется только одна клетка таблицы, соответствующая минимальной стоимости и исключается из рассмотрения только одна строка (поставщик) или один столбец (потребитель). Очередную клетку, соответствующую, заполняют по тем же правилам, что и в методе северо-западного угла. Поставщик исключается из рассмотрения, если его запасы груза использованы полностью. Потребитель исключается из рассмотрения, если его запросы удовлетворены полностью. На каждом шаге исключается либо один поставщик, либо один потребитель. При этом если поставщик еще не исключен, но его запасы равны нулю, то на том шаге, когда от данного поставщика требуется поставить груз, в соответствующую клетку таблицы заносится базисный нуль и лишь затем поставщик исключается из рассмотрения. Аналогично с потребителем.

Итак, рассмотрим решение транспортных задач.

Задача № 7.1.21. В следующих транспортных задачах необходимо найти такие объёмы перевозок продукции от поставщиков к потребителям при которых общие затраты на перевозку будут минимальными. В таблицах заданы объёмы запасов продукции у поставщиков (Ai), объемы потребности в продукции потребителей (Bj ) и удельные затраты на перевозку единицы продукции от поставщиков к потребителям (пересечение соответствующих строк и столбцов таблицы).

В таблице 11 представлены исходные данные задачи, в соответствии с вариантом 21.

Таблица 11 – Исходные данные задачи

Bj Ai		1	2
		36	117
1	79	1	7
2	168	6	4
3	42	4	7
4	90	3	5
5	76	1	1

Из исходных данных видно, что задача относится к закрытому типу так как, суммарный объем производства больше суммарного объема потребления.

Для того что бы решить эту задачу необходимо ввести фиктивного потребителя.

На рисунке 4.11 представлены формулы для решения задачи в MS Excel.

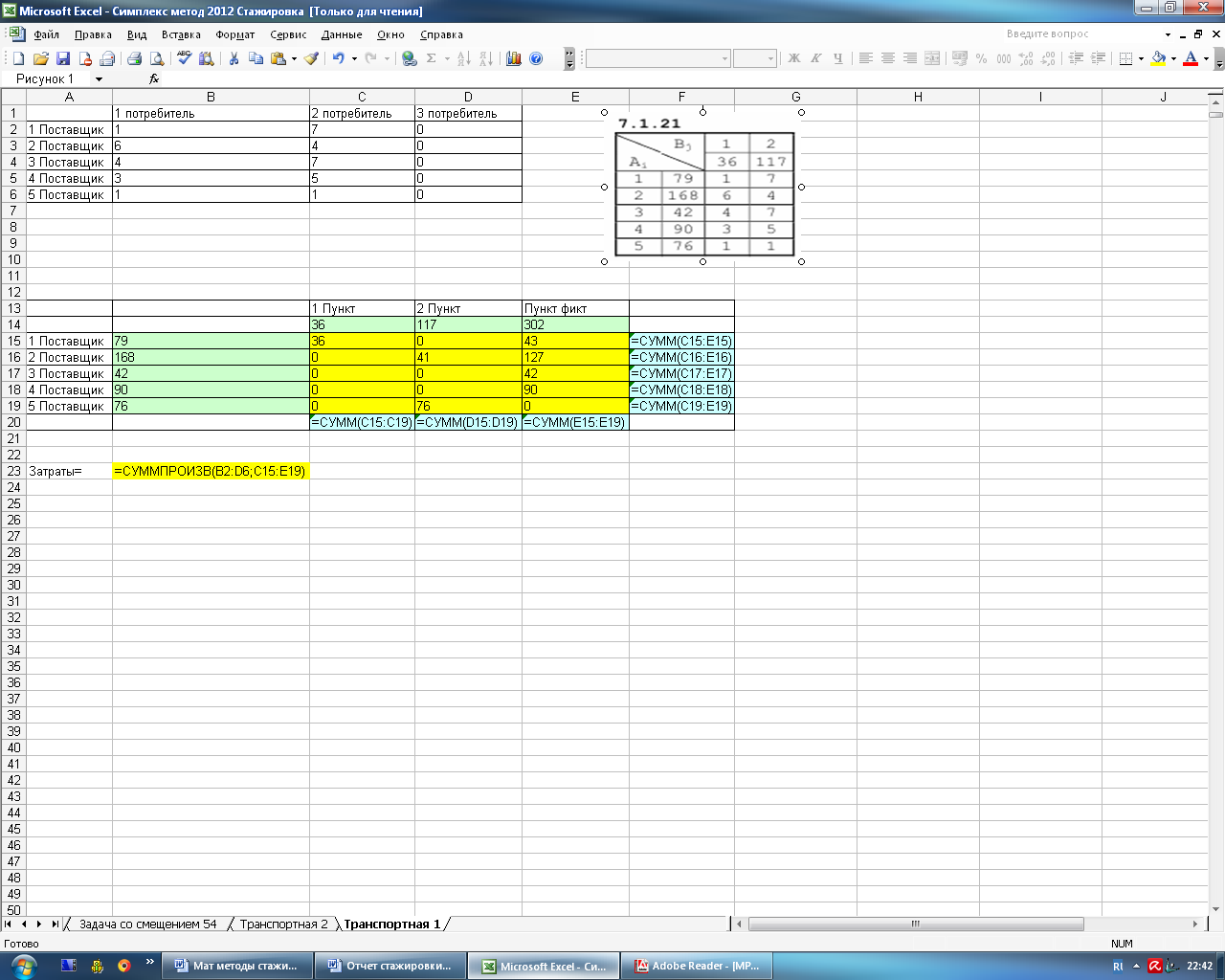
Рисунок 4.11 – Формулы, используемые для решения задачи

На рисунке 4.12 и 4.13 представлены окна поиска решений.

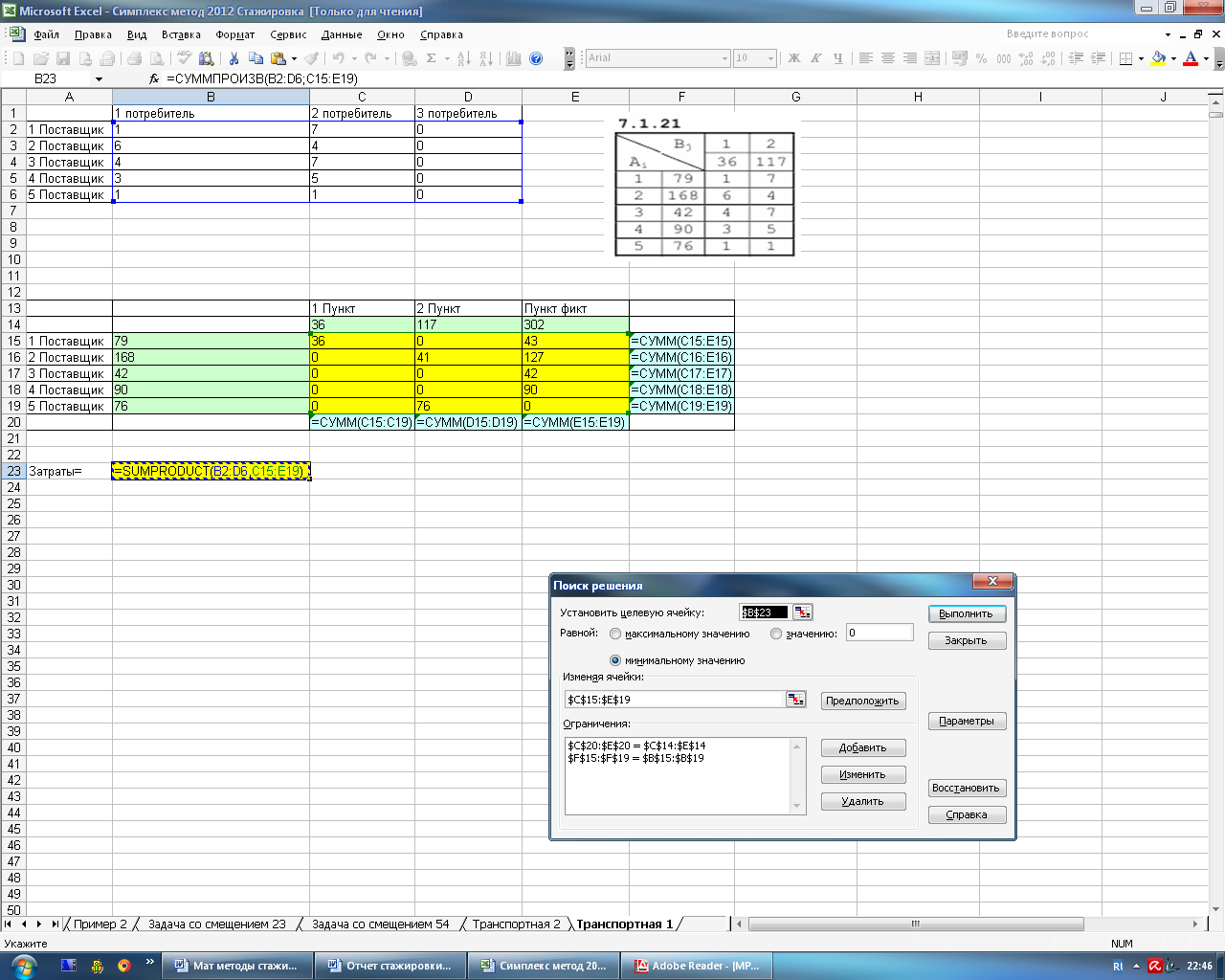
Рисунок 4.12 – Окно поиска решений

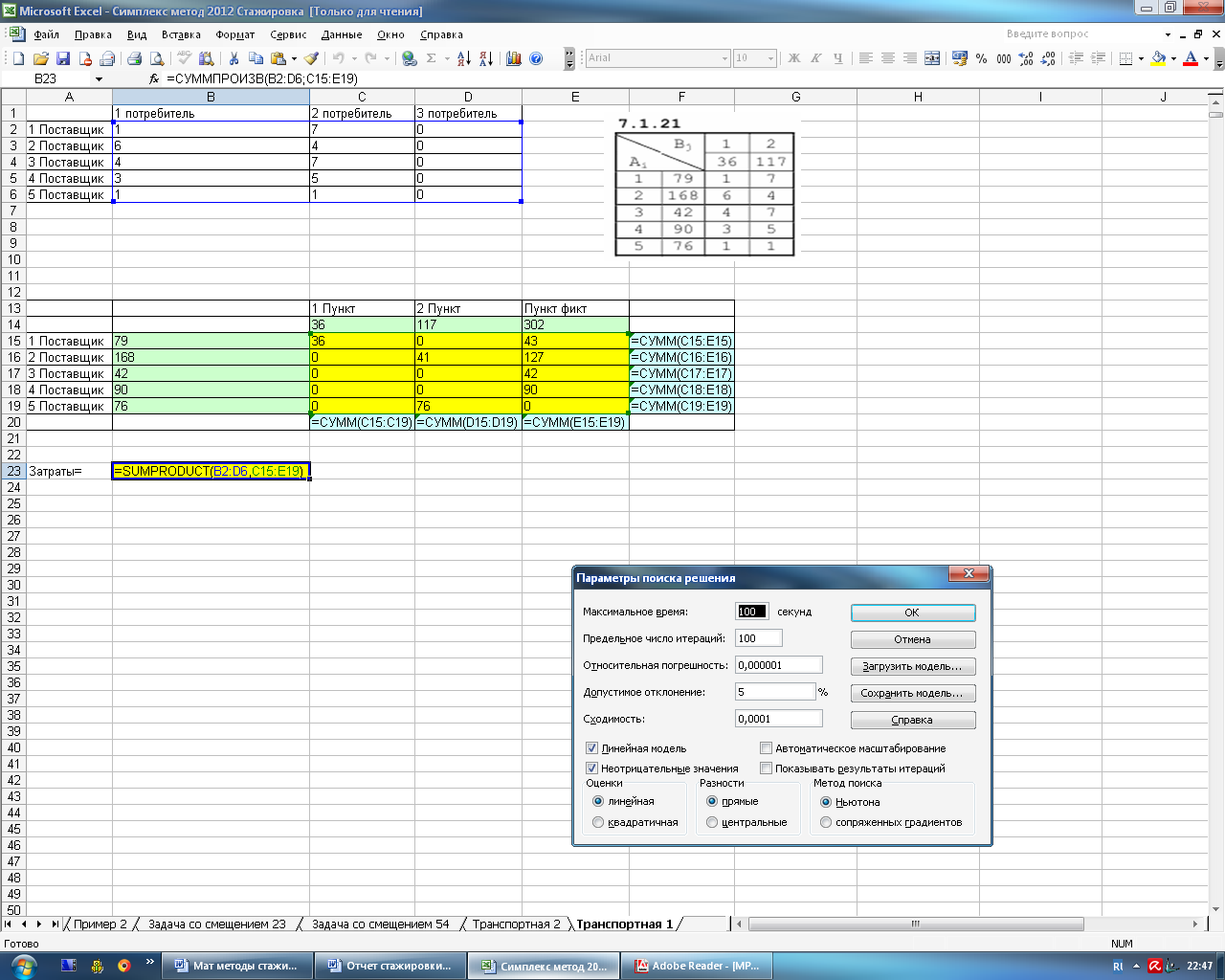
Рисунок 4.13 – Окно параметров поиска решений

На рисунке 4.14 представлен результат решения транспортной задачи.

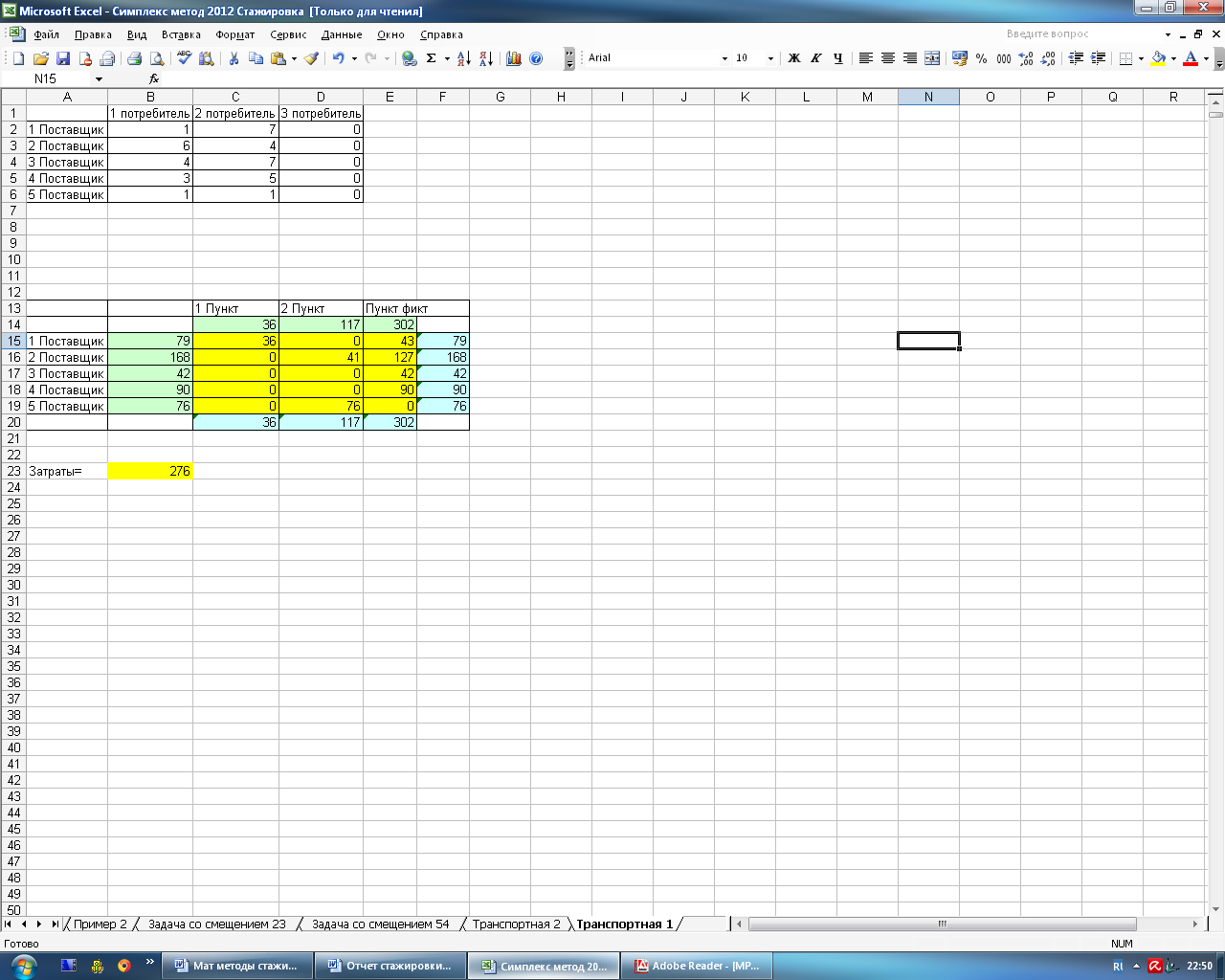
Рисунок 4.14 – Результат решения задачи

В результате решения задачи выяснилось, что минимальные затраты на перевозку продукции будут равны 276 денежным единицам.

Задача № 7.1.52. В следующей транспортной задаче необходимо найти такие объёмы перевозок продукции от поставщиков к потребителям при которых общие затраты на перевозку будут минимальными. В таблицах заданы объёмы запасов продукции у поставщиков (Ai), объемы потребности в продукции потребителей (Bj ) и удельные затраты на перевозку единицы продукции от поставщиков к потребителям (пересечение соответствующих строк и столбцов таблицы).

В таблице 12 представлены исходные данные задачи, в соответствии с вариантом 21.

Таблица 12 – Исходные данные задачи

Bj Ai		1	2	3	4
		119	145	107	39
1	51	2	4	0	5
2	111	0	7	4	5
3	138	0	5	7	5

Данная задача относится к открытому типу, так как суммарный объем производства меньше суммарного объема потребления. Транспортную задачу открытого типа предварительно необходимо свести к закрытой, для чего вводится фиктивный пункт производства.

На рисунке 4.15 представлены формулы для решения задачи в MS Excel.

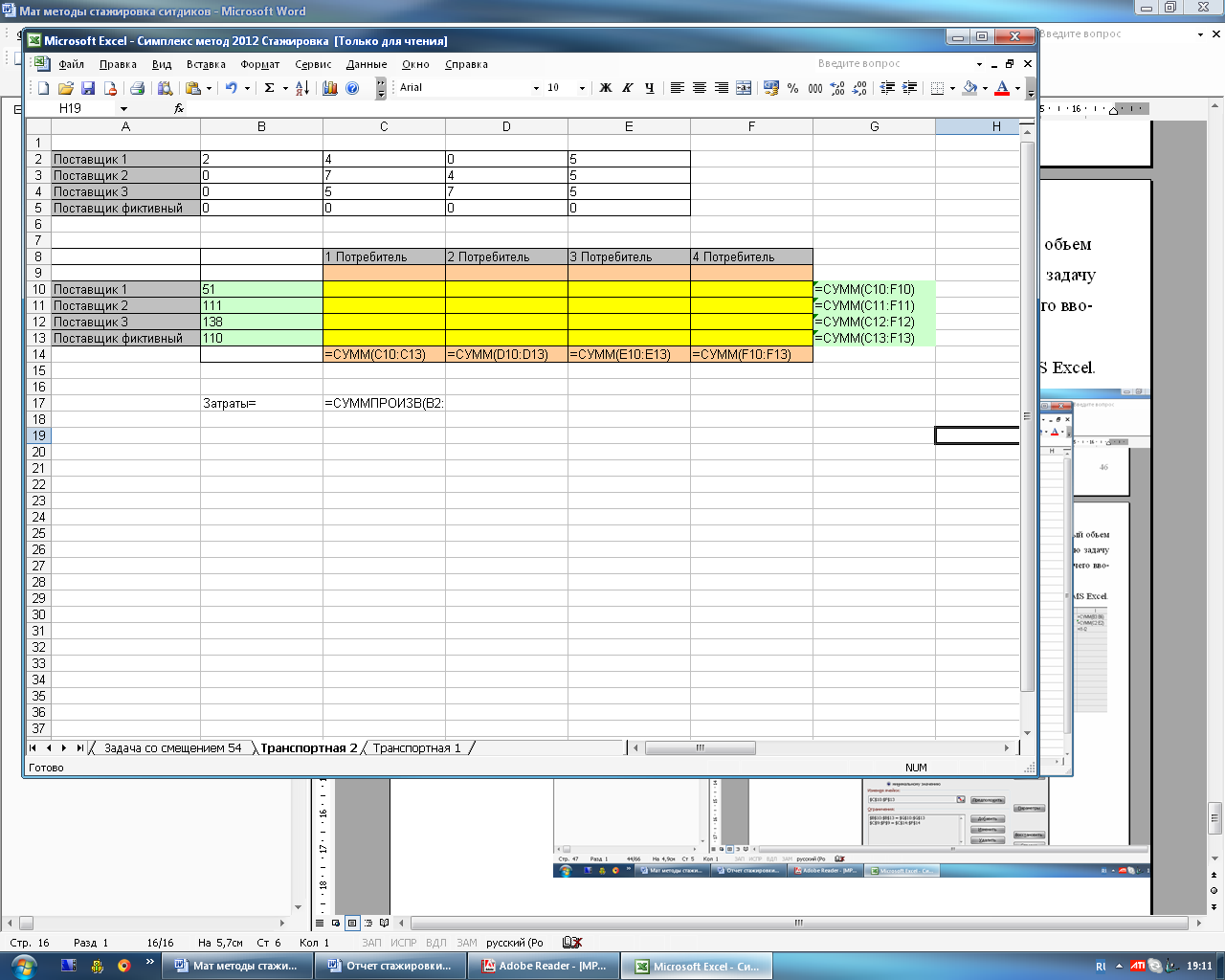
Рисунок 4.15 – Формулы, используемые для решения задачи

На рисунке 4.16 и 4.17 представлено окно поиска решений.

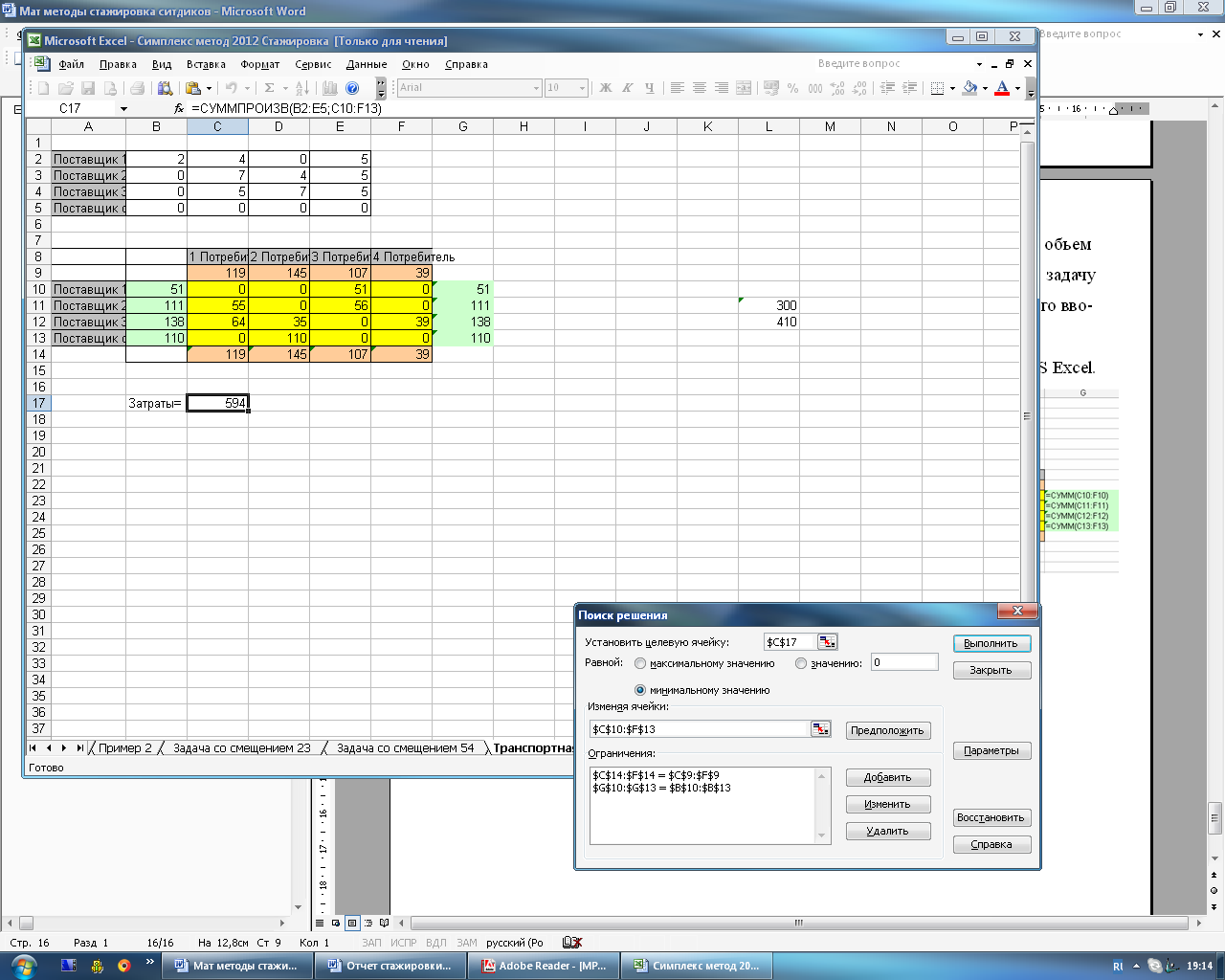
Рисунок 4.16 – Окно поиска решений

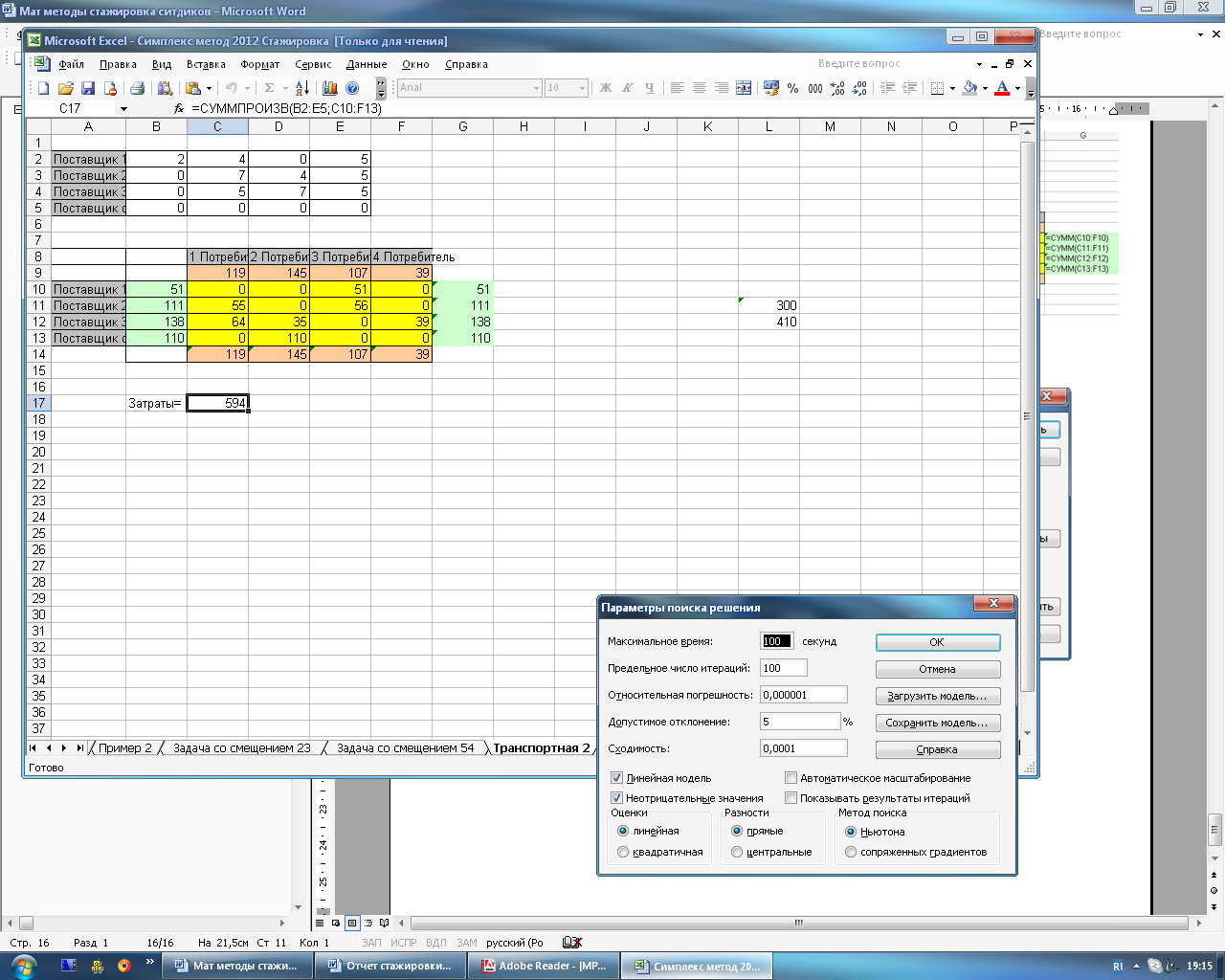
Рисунок 4.17 – Окно параметров поиска решений

На рисунке 4.18 представлен результат решения транспортной задачи.

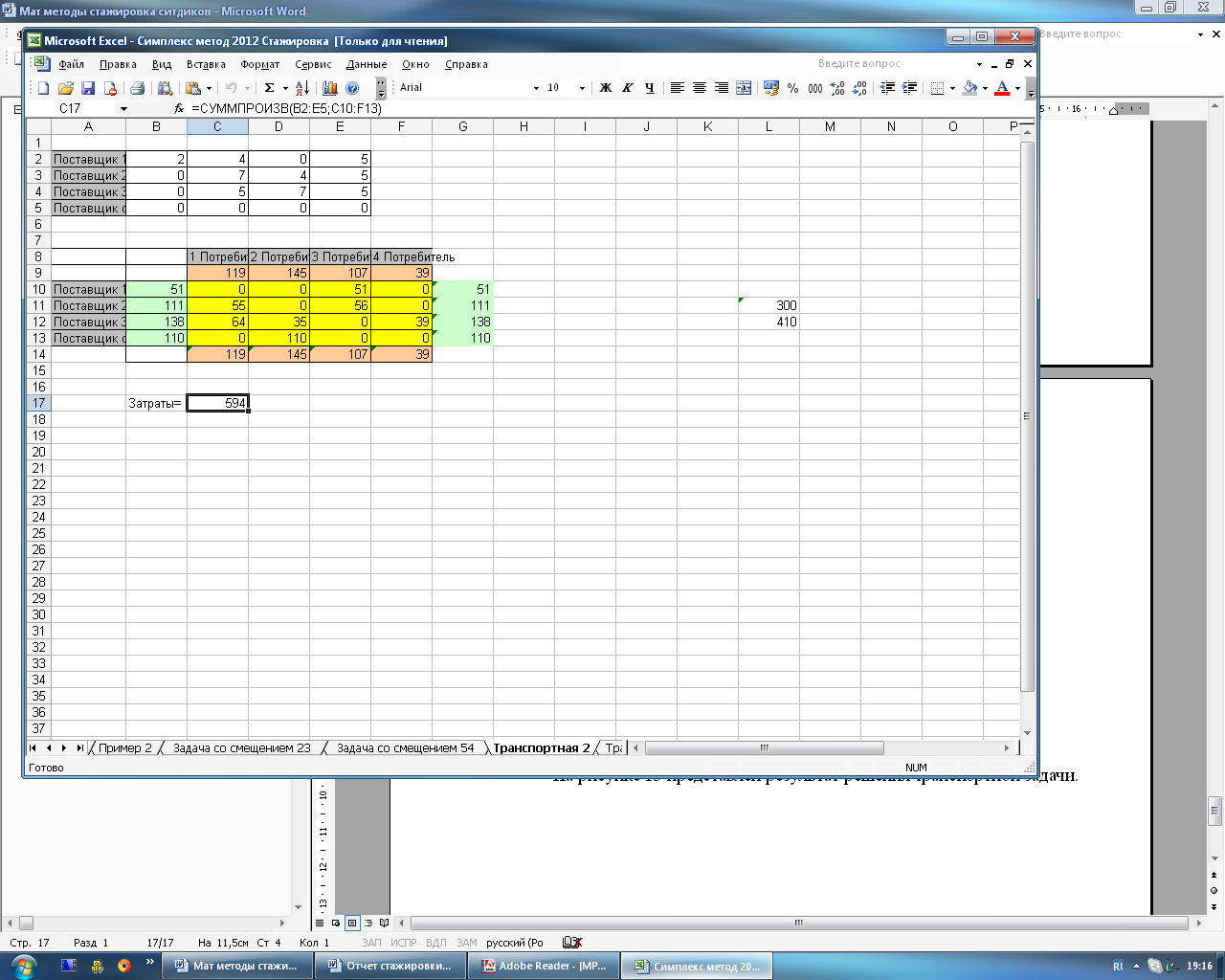
Рисунок 4.18 – Результат решения транспортной задачи

В результате решения задачи выяснилось, что минимальные затраты на перевозку продукции будут равны 594 денежным единицам.

Далее необходимо рассмотреть решения данных задач с помощью математического пакета Maple.

Математический пакет Maple – программный пакет, система компьютерной алгебры. Позволяет легко найти решение оптимизационной задачи.

На рисунках 4.19 и 4.20 представлено решение задач с помощью математического пакета Maple.

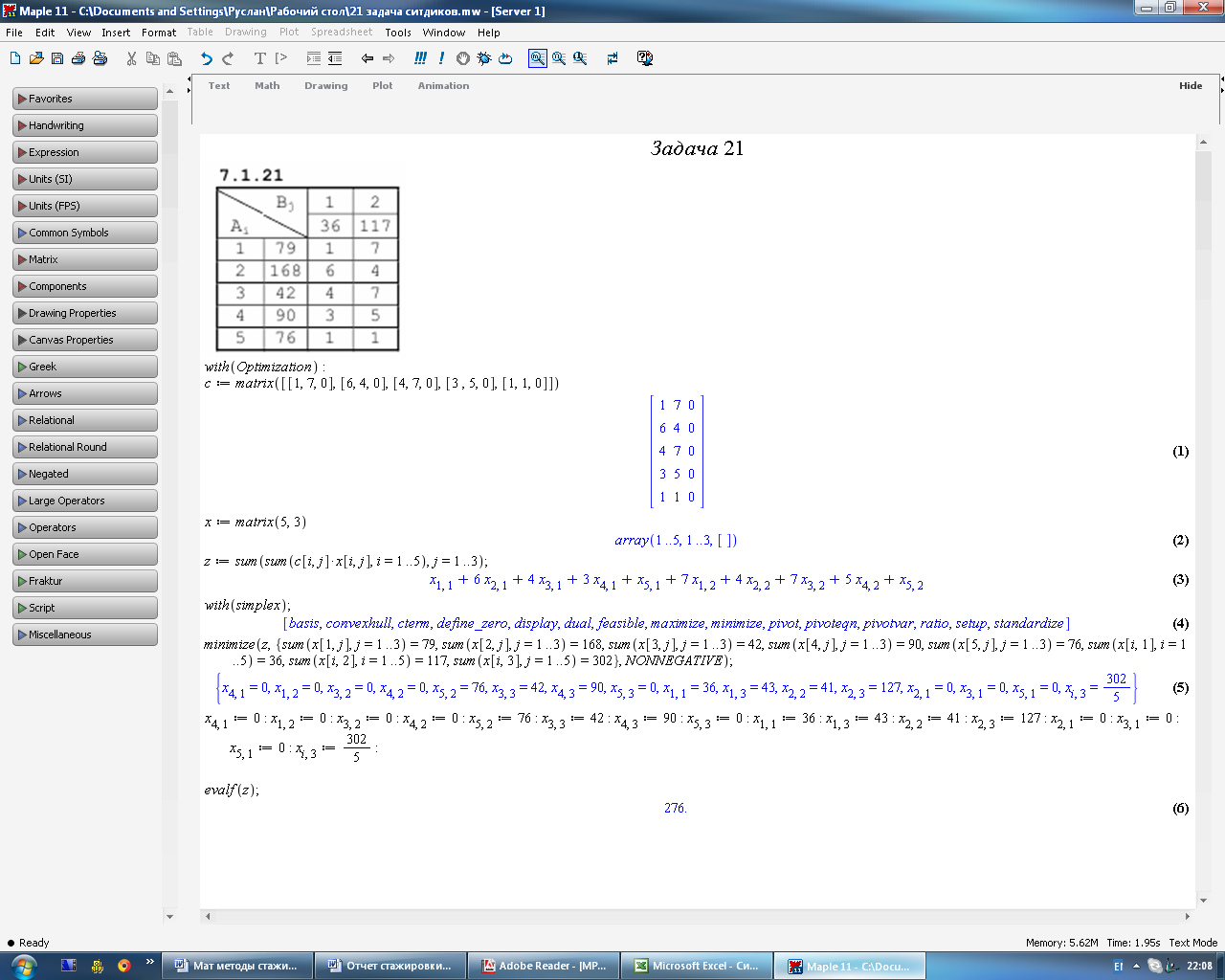
Рисунок 4.19 – Пример решения задачи № 7.1.21 с помощью математического пакета Maple

Результат решения задачи с помощью математического пакета Maple и MS Excel сошлись, и минимальные затраты на перевозку продукции равны 276 денежным единицам.

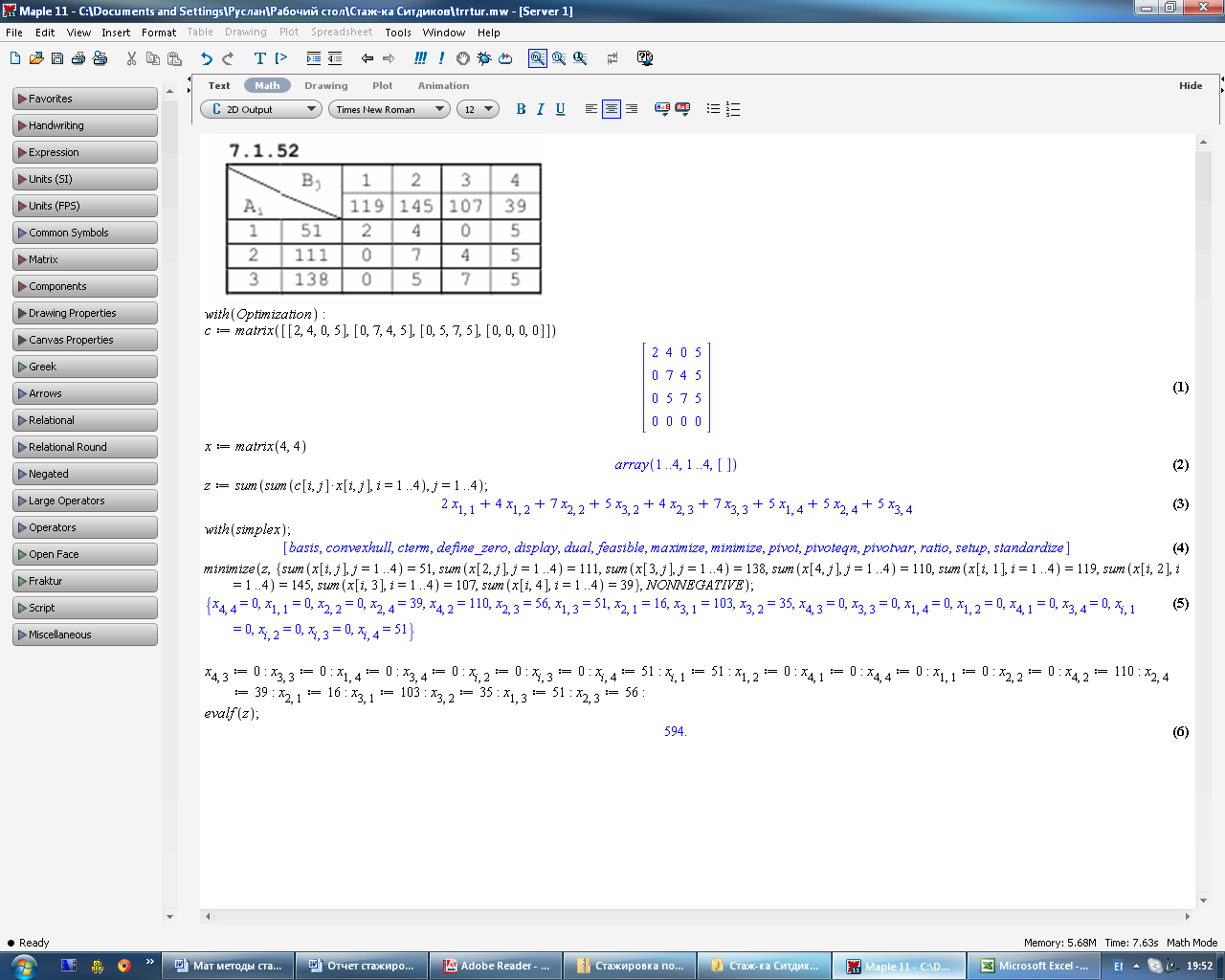
Рисунок 4.20 – Пример решения задачи № 7.1.52 с помощью математического пакета Maple

Результат решения задачи с помощью математического пакета Maple и MS Excel сошлись, и минимальные затраты на перевозку продукции равны 594 денежным единицам.