системы итерированных функций и фракталы
.docМинистерство образования и науки Российской Федерации
Министерство образования и науки Республики Татарстан
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«КАЗАНСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. А.Н.ТУПОЛЕВА-КАИ»
XX ТУПОЛЕВСКИЕ ЧТЕНИЯ
Международная молодежная
научная конференция
Казань, 22-24 МАЯ 2012Г.
СЕКЦИЯ 4.4. ТЕОРИТИЧЕСКАЯ И ПРИКЛАДНАЯ МАТЕМАТИКА И МЕХАНИКА.
Председатель: В.И.Анфиногентов, д.ф.-м.н., профессор каф. СМ
Секретарь: Н.Т.Валишин, к.ф.-м.н., доцент каф. СМ
Тема доклада: «Системы итерированных функций и фракталы»
Авторы: С.Э.Зинатуллина, Р.А.Баков. 1 курс. Гр. 6108
Научный руководитель: Н.И.Гоза, к.ф.-м.н., доцент
План доклада:
-
Фракталы.
-
Афинные отображения.
2.1. Итерирование двумерных отображений. Итерации точек плоскости.
2.2. Итерирование двумерных отображений. Итерации множеств на плоскости.
2.3. Образы систем функций.
3. Итерации систем функций.
3.1. Итерации систем функций. Сжимающие отображения.
«Системы итерированных функций и фракталы»
Авторы: С.Э.Зинатуллина, Р.А.Баков.1 курс. Гр. 6108
Научный руководитель: Н.И.Гоза, к.ф.-м.н., доцент
-
Фракталы
Фракта́л (лат. fractus — дроблёный, дробный, подобный) — геометрическая фигура, обладающая свойством самоподобия, то есть составленная из нескольких частей, каждая из которых подобна всей фигуре целиком. В математике под фракталами понимают множества точек в евклидовом пространстве, имеющие дробную метрическую размерность (в смысле Минковского или Хаусдорфа), либо метрическую размерность, отличную от топологической.
Первые примеры самоподобных множеств с необычными свойствами появились в XIX веке. Термин «фрактал» был введён Бенуа Мандельбротом в 1975 году и получил широкую популярность с выходом в 1977 году его книги «Фрактальная геометрия природы».
Рассмотрим некоторые примеры фракталов.
Множество Кантора — нигде не плотное несчётное совершенное множество. Модифицировав процедуру, можно также получить нигде не плотное множество положительной длины.
Треугольник Серпинского — аналог множества Кантора на плоскости.
Кривая Пеано — непрерывная кривая, проходящая через все точки квадрата.
Примеры фрактальных кривых:
Кривая дракона, Кривая Леви,
Кривая Минковского, Дерево Пифагора.
Фракталы в комплексной области.
Множества Жюлиа
Биоморфы — фракталы, построенные на основе комплексной динамики и напоминающие живые организмы.
Природные объекты часто имеют фрактальную форму. Для их моделирования могут применяться стохастические (случайные) фракталы.
Стохастические фракталы
-
Афинные отображения
Аффинным
отображением (аффинным преобразованием
плоскости)
называется такое отображение, которое
любые три точки прямой А
,
А
,
А
переводит в три точки А
,
А
,
А
,
также лежащие на одной прямой, причем
сохраняется простое отношение трех
точек, т.е. (А
А
,
А
)=(
А
А
,
А
).
Примерами аффинного преобразования плоскости являются подобия, параллельный перенос, поворот, движение, осевая симметрия или композиция этих преобразований.
Проверим, как работает аффинное отображение f(x;y)=(x-y;x+y) на примере квадрата (0 x, y 1).
Вершины квадрата: (0;0), (0;1), (1;0), (1;1). Найдем образы вершин квадрата при заданном отображении.
f(0;0)= (0;0), f(0;1)= (-1;1), f(1;0)= (1;1), f(1;1)= (0;2)
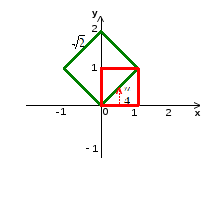
Видим,
что данное аффинное отображение можно
рассматривать как поворот на угол
против часовой стрелки и умножение на
.
Аффинные отображения обладают следующими важными свойствами:
1. При аффинном отображении прямые переходят в прямые, при этом параллельные переходят в параллельные, а пересекающиеся в пересекающиеся.
2. При аффинном отображении полуплоскости переходят в полуплоскости.
3. При аффинном отображении лучи переходят в лучи.
4. При аффинном отображении отрезки переходят в отрезки.
5. При аффинном отображении углы переходят в углы.
-
Итерирование двумерных отображений. Итерации точек плоскости
Переход от (х
;у
)
к f(х
;у
)
называется итерацией.
Пусть (х
;у
)
- начальная точка,
(х
;у
)
(х
;у
)=
f(х
;у
)-
первая итерация точки (х
;у
),
(х
;у
)=
f(х
;у
)=
f
(f
(х
;у
))=
f
(2)(
х
;у
)-
вторая итерация точки (х
;у
),
(х
;у
)=
f
((х
;у
)=
f
(f
(f
(х
;у
)))=
f
(3)(
х
;у
)-
третья итерация точки (х
;у
),
…
(х
;у
)=
f
(х
;у
)=
f
(f
(f
(…(f
(х
;у
)…)))=
f
(n)(
х
;у
)-n-я
итерация точки (х
;у
),
…
Данный процесс построения итераций называется итерационным процессом.
-
Итерирование двумерных отображений. Итерации множеств на плоскости
Пусть А – подмножество Евклидовой плоскости, а f(х, у) – некоторое двумерное отображение.
А
=
f
(А)- первая
итерация множества А (образ множества
А при двумерном отображении
f
),
А
=
f
(А
)=
f
(f
(А))= f
(2)(
А)- вторая
итерация множества А,
А
=
f
((А
)=
f
(f
(f
(А)))= f
(3)(
А)- третья
итерация множества А,
…
А
=
f
(А
)=
f
(f
(f
(…(f
(А)…)))= f
(n)(
А)- n-я
итерация множества А,
…
-
Образы систем функций
Пусть задано семейство из n отображений: f1 , f2 , …, fn, и пусть А – некоторое подмножество Евклидовой плоскости. Найдем образ множества А при каждом из этих отображений: f1(А), f2(А), …, fn(А).
Образом множества А относительно системы функций называется объединение всех образов f1(А), f2(А), …, fn(А).
Обозначение: Т(А)= f1(А) f2(А) …fn(А).
Другими словами, Т(А) состоит из всех точек, которые находятся хотя бы в одном из образов f1(А), f2(А), …, fn(А).
-
Итерации систем функций
Итерационный процесс для систем функций.
Пусть задано семейство из n отображений: f1 , f2 , …, fn и пусть А – подмножество Евклидовой плоскости.
Т(А)= f1
(А)
f2
(А)
…
fn
(А) – образ системы функций. Аналогично
тому, как мы определяли итерационный
процесс при двумерном отображении,
можно определить итерационный процесс
для системы двумерных отображений.
Т(А)= f1
(А)
f2
(А)
…
fn
(А) – первая итерация,
Т2(А)=
Т(Т(А))= f1
(Т(А))
f2
(Т(А))
…
f n
(Т(А)) – вторая итерация,
…
Тn (А)= Т(Тn-1 (А)) - n-я итерация.
Рассмотрим пример: построить образ точки О(0,0) в результате трёх итераций заданной системы функций.
;
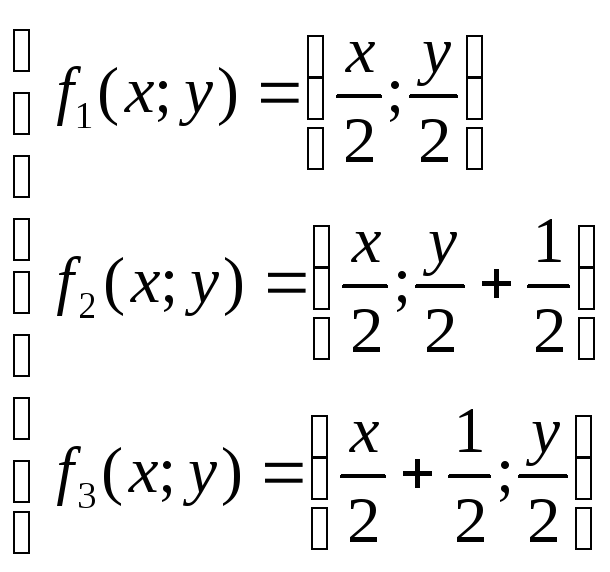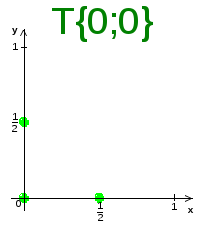
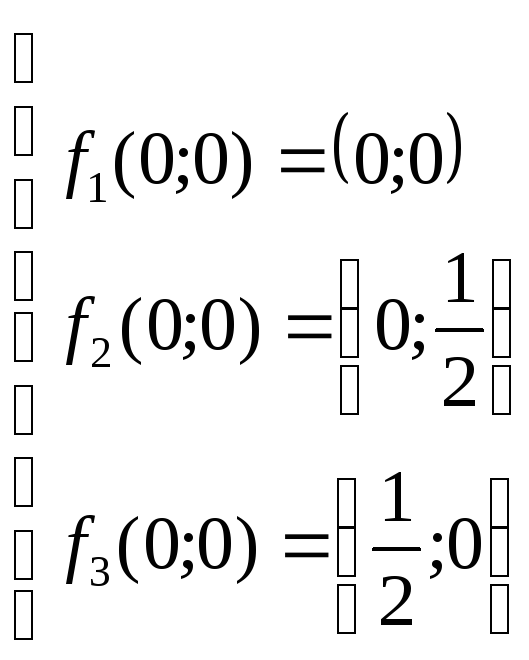; Т({0;0})={(0;0),
(0;
),
(
;0)}
;
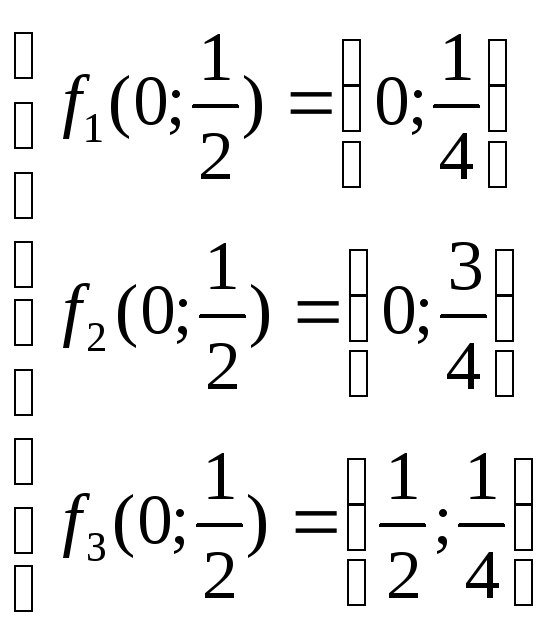
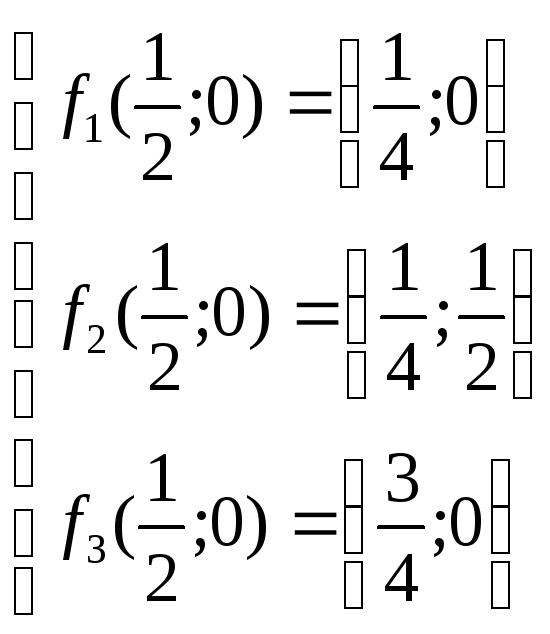
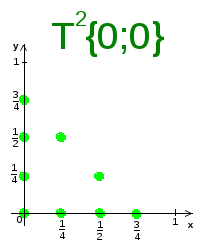
Т2({0;0})={(0;0), (0;
),
(
;0),
(0;
),
(0;
),
(
;
),
(
;0),
(
;
),
(
;0)}
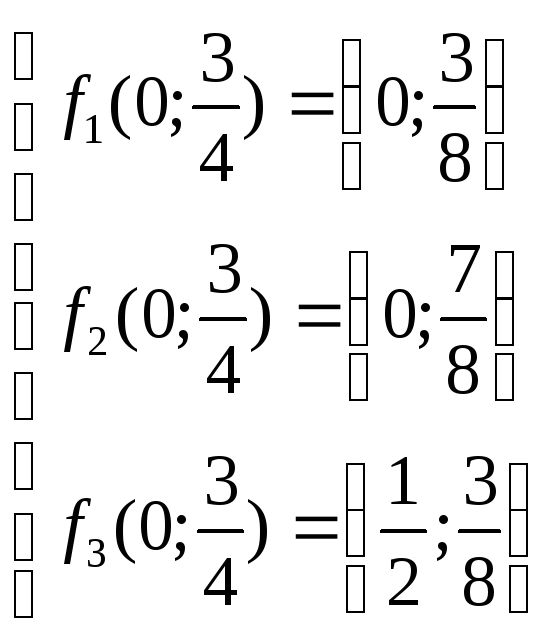
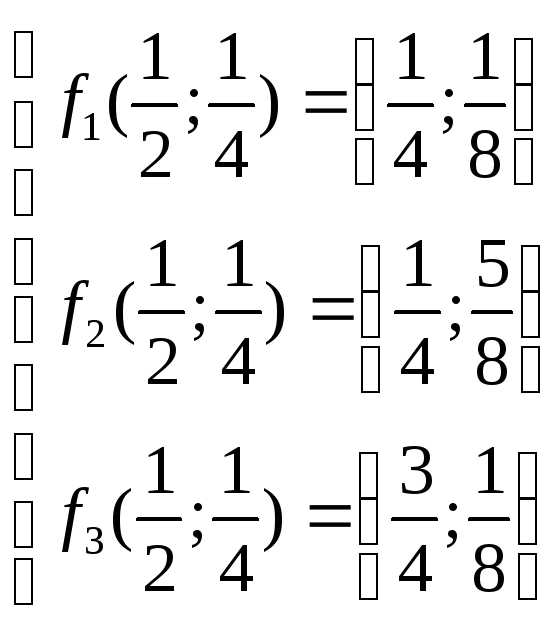
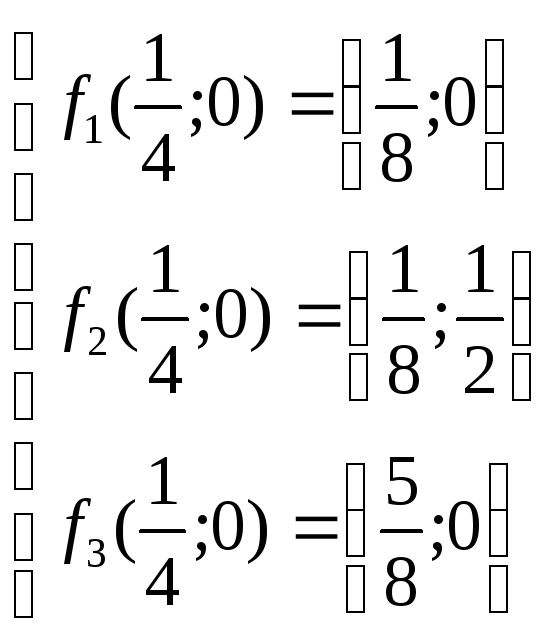
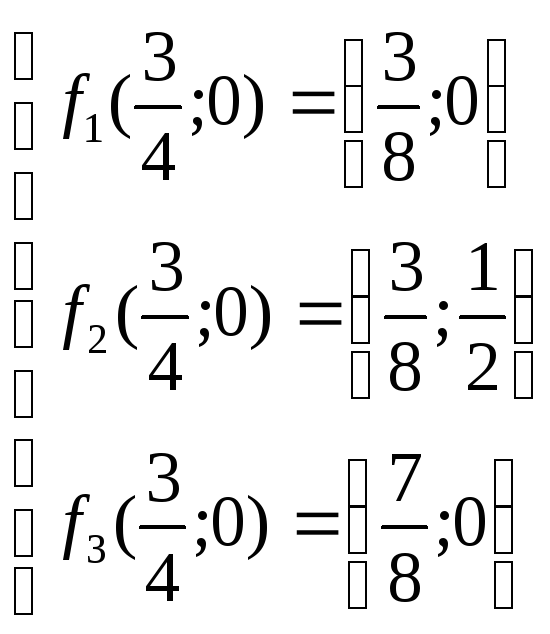
Т3({0;0})={(0;0), (0;
),
(
;0),
(0;
),
(0;
),
(
;
),
(
;0),
(
;
),
(
;0),
(0;
),
(0;
),
(
;
),
(0;
),
(0;
),
(
;
),
(
;
),
(
;
),
(
;
),
(
;0),
(
;
),
(
;0),
(
;0),
(
;
),
(
;0),
(
;
),
(
;
),
(
;
)}
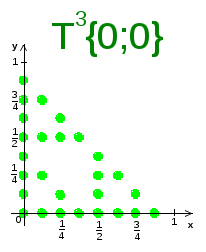
Если продолжить этот итерационный процесс, то мы получим в предельном случае Косынку Серпинского.
-
Итерации систем функций. Сжимающие отображения
Аффинное
отображение
f:
(x;y)
(аx+by+e;cx+dy+g)
является сжимающим, если (ad
+bc)
+1-a
-b
-c
-d
>0.
Аффинные
отображения популярны из-за идеи
сохранения сложного изображения, как
набора чисел для коэффициентов a,
b,
c,
d,
e,
g.
Например, чтобы построить притягивающие
точки для системы
,
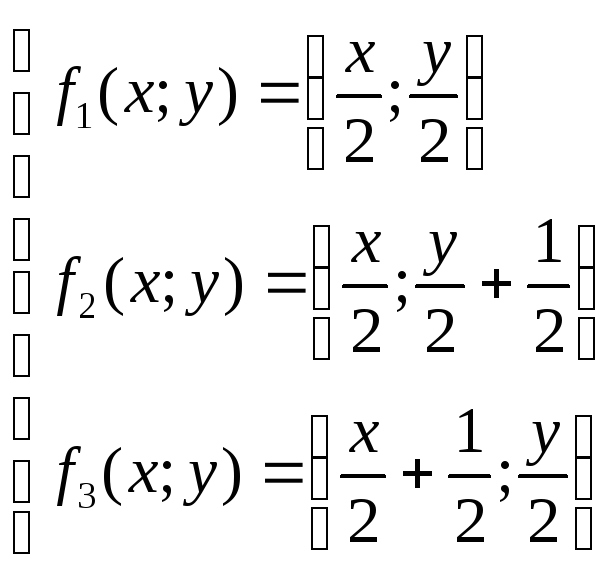нам будут нужны три функции и, таким образом, восемнадцать чисел для коэффициентов, шесть для каждой функции.
Можно рассматривать и обратную задачу, а именно, находить коэффициенты для желаемого поведения отображения.
Примеры нахождения аффинных отображений.
Найти коэффициенты аффинного отображения f, если f(0;0)=(0.6;0.8), f(0;1)= (0.6;1), f(1;0)= (0.8;0.8). Определить, является ли оно сжимающим.
f
- аффинное
f(x;y)=(аx+by+e;cx+dy+g)
Составим системы уравнений:
-
f(0;0)= (0.6;0.8)
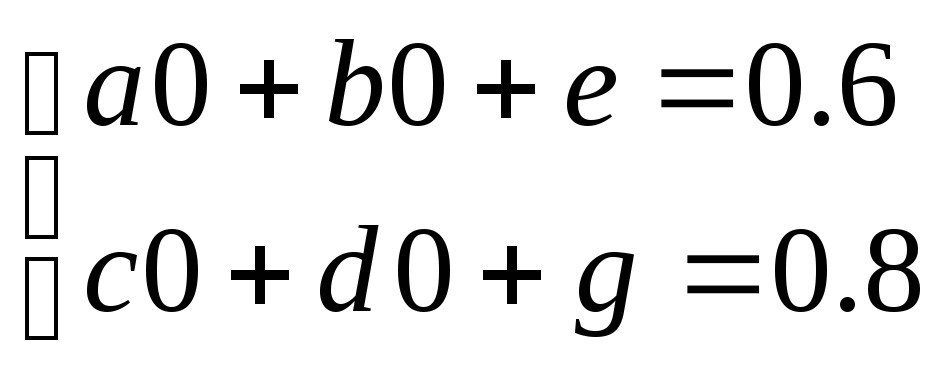
e=0.6,
g=0.8 -
f(0;1)= (0.6;1)
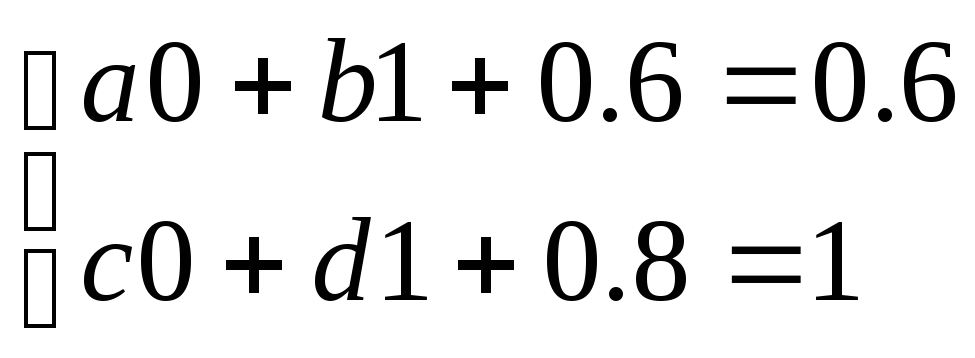
b=0,
d=0.2 -
f(1;0)= (0.8;0.8)
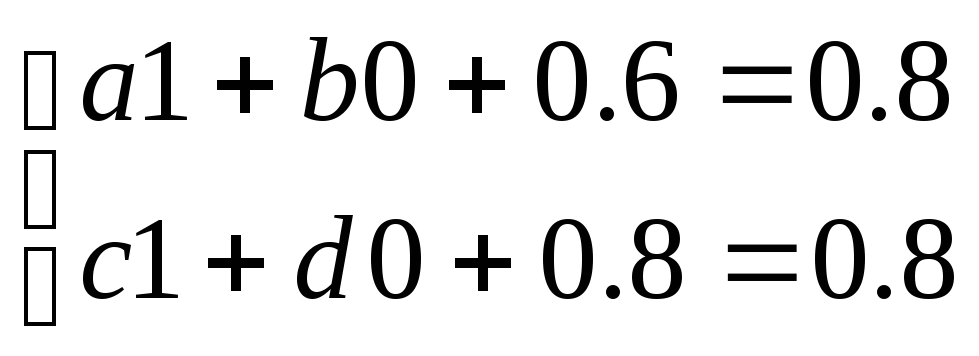
a=0.2,
c=0
f(x;y)=(0.2x+0.6;0.2y+0.8)
Проверим, является ли f сжимающим отображением?
f
– сжимающее, если (ad
+bc)
+1-a
-b
-c
-d
>0:
(0.2 · 0.2
)
+1-0.2
-0.2
=(1-0.2
)
>0
f
- сжимающее отображение.
Таким образом, итерированные системы функций позволяют строить различные геометрические фракталы на плоскости. Особенно интересны в этом плане итерации систем функций, являющихся сжимающими отображениями.