28. Метод отсечения, общая постановка задачи.

Имеем задачу целочисленного программирования записанную в канонической форме:

(1)

при ограничениях:

(2)

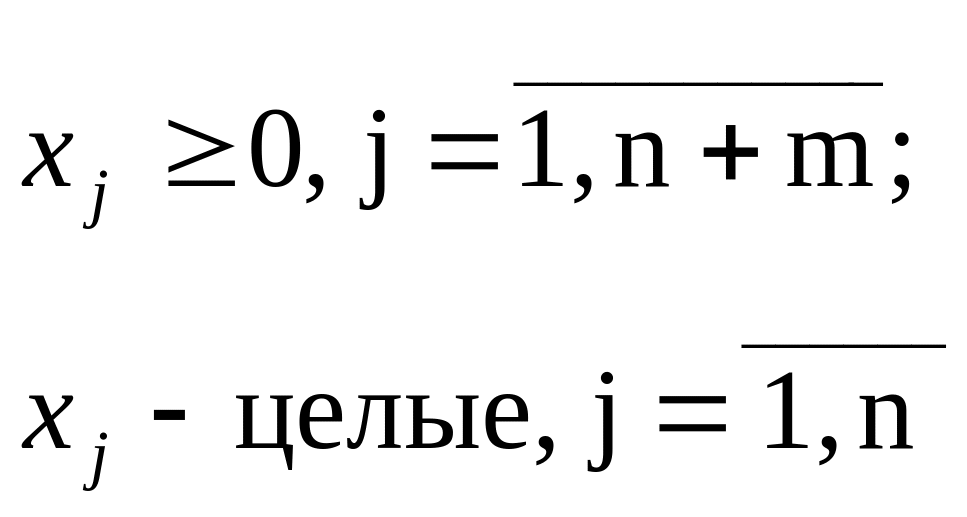(3) (4)

Здесь -исходные переменные задачи;

- дополнительные переменные задачи;

При решение необходимо иметь ввиду, что т.к. оптимальное решение определяется пересечением n гиперплоскостей, то таких гиперплоскостей существует не больше чем это необходимо(часть этих плоскостей могут быть ограничениями исходной задачи). Каждое текущее решение задачи можно представить в виде таблице неравенств:

	1			…
f(X)				…
				…
				…
……..
				…

Предполагается , что все в исходной таблице целые все дополнительные переменные также должны быть целыми неотрицательными числами. Можно показать, что если -выпуклый многогранник , -множество его целых точек , -выпуклая линейная оболочка множества , то является целочисленным многогранником. Непосредственно построение - сложная задача, является основной задачей методов отсечения.

Алгоритм состоит из следующих процедур:

1. Решается исходная задача линейного программирования (1)-(3) каким-либо методом

2. Получение оптимального решения ЗЛП(задача линейного программирования), если оно существует- проверить на условие целочисленности. Если условие выполняется оптим. решение ЗЛП является одновременно оптимальным решением целочисленного ЗЛП(ЦЗЛП). Если условия (4) [x-целое] не выполняется хотя бы для одной переменной , то перейдем к следующему этапу

3. Строим специальное дополнительное ограничение, позволяющее отсечь часть области R; в котором содержится оптим. решение ЗЛП и не содержится допустимого ЦЗЛП.

Подобный процесс построения доп. ограничений повторим до тех пор пока :

а) не будет доказана неразрешимость ЦЗЛП

б) либо пока не получим целочисленное решение

Примечание: дополнительные ограничения должны быть линейны;

Таким образом, любое неравенство пригодное для этой цели(см.Примечание) и имеющее вид должно удовлетворять условиям правильного отсечения:

а) условию отсечения, т е оптимальному решению предыдущего ЗЛП не удовлетворяющего этому неравенству

б) любое допустимое решение ЦЗЛП удовлетворяет этому неравенству

30. Метод отсечения, смешанный алгоритм.

2.2 Смешанный алгоритм Гомори

Этот алгоритм является в основном повторением циклического алгоритма Гомори, но правило получения отсечения из порождающей строки другое. В названии алгоритма отражается тот факт, что с его помощью возможно решать задачи частично целочисленного линейного программирования. Естественно, он позволяет решать и задачи целочисленного линейного программирования.

Итак, задана задача частично целочисленного программирования: найти максимум

(2.10)

при условиях

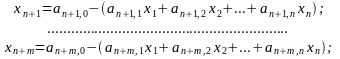(2.11)

(2.12)

(2.13)

Решим эту задачу как ЗЛП. Если в результате этого получено оптимальное решение, в котором все свободные члены по строкам не меньше нуля, и все переменные, на которые наложено требование целочисленности, имеют целые значения, то, следовательно, получено оптимальное решение ЗЧЦЛП. Допустим, что на переменную x₁ наложено требование целочисленности, но в оптимальном решении ЗЛП ей соответствует a_i0>=0 и нецелость. Запишем эту строку, опустив индекс строки:

(2.14)

поскольку x должно быть целым, то из (2.14) следует, что

, p - целое. (2.15)

Пусть коэффициенты a_j(j∈ N) разбиты на два множества . Тогда .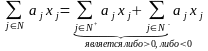

Если , то левая часть принимает значения {a₀}, {a₀}+1, (a₀}+2 и т.д. Тогда (2.16)

Если то левая часть (должна) принимает значения -1+{a₀}; -2+{a₀} и т.д.

При этом

Умножим обе части этого неравенства на .

Получим (2.17)

Сложив (2.16) и (2.17), получим

(2.18)

И этому неравенству должно удовлетворять любое целочисленное решение задачи (2.10) - (2.13). Текущее решение ему не удовлетворяет, так как при x_j=0 (j∈ N) получим из (2.18) 0>={a₀}. Итак, при получении (2.18) допускалось, что условие целочисленности наложено только на переменную x в левой части (2.14), а на все переменные x_j(j∈ N) налодено только требование неотрицательности (т.е. при любых целых или нецелых x_j j∈ N). Тогда, введя дополнительную переменную, (2.17) запишем в виде (2.19)

Затем это ограничение добавляем к оптимальному решению ЗЛП, после чего она перестанет быть допустимой; затем решаем эту расширенную ЗЛП с помощью двойственного симплекс-метода с использованием строки (2.19) в качестве ведущей строки и т.д.

Вообще общей целью является получение как можно более сильного ограничения (2.19), т.е. желательно сделать коэффициенты a_j(j∈ N⁺) и как можно меньшими (тогда, если эти элементы будут разрешающими, при пересчете произойдут большие изменения чисел). Это возможно, если учесть, что на некоторые x_j(j∈ N) наложено требование целочисленности.

Поскольку (2.18) получено из (2.15), то рассмотрим в последнем слагаемое a_kx_k, где на x_k наложено требование целочисленности. Естественно, что увеличение или уменьшение a_k на целое число не изменит справедливости выражения (2.15). Минимально возможным (допустимым) числом, полученным из a_k>=0 (k∈ N⁺), является {a_k}; а для a_k<0 наименьшую величину дает значение .

Желательно было бы увеличивать или уменьшать a_k в выражении (2.15) на целое число таким образом, чтобы получать минимальное значение коэффициентов в (2.19), т.е. нужно находить минимум из , так как обе эти величины положительны.

Для справки: функция φ(z) = z/(1-z) возрастает с ростом z при z<1. тогда ясно, что и . Если , или, если записать по-другому, , если и , если . Таким образом, из уравнения (2.19) получим (2.20)

Уравнение (2.20) подписывается к таблице решения, содержащей оптимальное решение ЗЛП, а затем решается задача максимизации при дополнительном ограничении.

При определенных ограничениях на возможные формы записи задачи (2.10) - (2.13) доказывается конечность этого алгоритма при решении задачи. Но обычно считают, что алгоритм позволяет получить искомое решение задачи при произвольной её записи (при произвольной записи функции цели).

Естественно, что этот алгоритм можно применять и для задач целочисленного линейного программирования, т.е. когда n₁=n. Для таких задач условие (2.20) приобретает вид

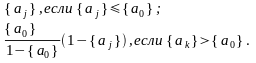
Использование подобных ограничений при решении ЗЦЛП обычно сокращает число шагов, необходимых для решения задачи, по сравнению с ограничением, введенным в 2.1.