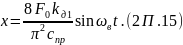2.12. Примеры и задачи к главе 2

Пример 2.1

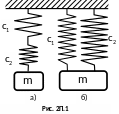Груз массой m подвешен на двух пружинах, как показано на рис. 2П.1, а и б.

Определить:

1. Эквивалентный коэффициент жёсткости системы и частоту вертикальных колебаний груза, если коэффициенты жёсткости пружин равны с₁ и с₂.

2. Эквивалентный коэффициент жёсткости системы и частоту вертикальных колебаний груза, если коэффициенты жёсткости пружин равны с₁= с₂.

Решение:

1. В случае, показанном на рис. 2П.1, а, статическое перемещение груза массой m равно

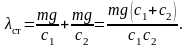
Э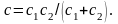 квивалентный коэффициент жёсткости равен

Круговая частота собственных колебаний в соответствии с формулой (2.32) равна

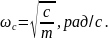
Частота собственных колебаний в Гц

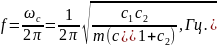
2. В случае, показанном на рис. 2П.1, б

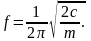
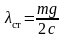
и

Пример 2.2

Колесо катится с постоянной горизонтальной скоростью v вдоль волнистой поверхности (рис. 2П.2). определить амплитуду вынужденных вертикальных колебаний груза массой m, связанного пружиной с осью колеса, если статическая деформация пружины под действием груза mg составляет λ_ст = 0,098 м, v = 18 м/с и поверхность профиля дороги задана уравнением s₁ =

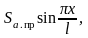
где S_а.пр = 0,025 м и l = 0,9 м. Массой колеса пренебречь.

Решение

В разделе 2.3.1 было принято, что возмущающая сила изменяется по гармоническому закону F=F₀·sinω_вt формула (2.45). В разделе 2.10 рассмотрены вынужденные колебания при произвольном перемещении опоры. В данном примере перемещение опоры задано кинематически по синусоидальному закону.

Рассмотрим вынужденные колебания системы с одной степенью свободы при кинематическом возбуждении по гармоническому закону перемещения опоры s(t) = S_а·sinω_вt,

где S_а – амплитуда перемещения опоры;

ω_в – круговая частота вынужденных колебаний опоры.

Уравнение вынужденных колебаний запишется

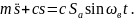
Разделив предыдущее уравнение на m, и вводя обозначения

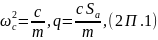
получим

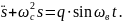
Это уравнение идентично ранее полученному уравнению (2.46) и, следовательно, установившиеся вынужденные колебания описываются аналогично выражению (2.51)

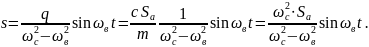
Или окончательно

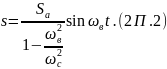
Определим частоту собственных колебаний груза массой m по формуле (2П.1). Жёсткость пружины по определению равна

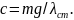Тогда круговая частота собственных колебаний массы m определится как ω_с² = g/λ_ст = 100 с^–2, или ω_с = 10 с^-1.

Центр о катящегося колеса совершает вертикальные колебания вследствие волнистости пути. Предполагая, что в начальный момент t = 0 точка соприкосновения колеса находится в начале координат

х = 0, и подставляя x = v·t, получаем для этих вертикальных колебаний уравнение

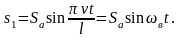
Вынужденные колебания груза определятся из уравнения (2П.2). подставим в него значения S_а = 0,025 м,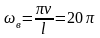 с^–1, ω_с² =100 с^–2. примем sinω_вt = –1, что соответствует максимальному перемещению колеса вверх. получим амплитуду вынужденных колебаний груза массой m, которая равна s = 0,025/(4π² – 1) = 0,00065 м. При данной скорости v вертикальные колебания колеса лишь в очень слабой степени передаются массе m в связи с большим значением вынужденной частоты. Вынужденная частота в Гц равна f = ω_в /2π = 10 Гц. Отношение ω_в/ω_с ≈ 6,28, а следовательно коэффициент динамичности k_д << 1, это говорит о том, что система находится далеко в зарезонансной зоне.

Если уменьшить вчетверо скорость v колеса, то есть снизить круговую частоту вынужденных колебаний, которая будет равняться ω_в = 5π с^–1 (f = 2,5 Гц), это приведёт к уменьшению коэффициента расстройки системы z = ω_в/ω_с = 1,57 в 4 раза и приближению режима работы системы к зоне резонанса. Амплитуда вынужденных колебаний массы m увеличится и будет равняться s = 0,025/(π²/4 –1) = 0,017 м. следовательно, коэффициент динамичности колебаний массы m возрастает более чем в 26 раз.

При дальнейшем уменьшении скорости v, соответствующей ω_в = ω_с, наступит резонанс, при этом будут происходить весьма сильные колебания массы m.

Пример 2.3

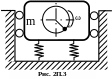Двигатель массой m = 45 кг, опирается на четыре винтовые пружины (рис. 2П.3), изготовленные из стальной проволоки диаметром d = 12 мм. Средний диаметр пружины D = 100 мм и число витков n = 10, угловая скорость вращения вала n = 1800 мин^-1, модуль сдвига G = 80·10⁹ Гпа, центробежная сила инерции от неуравновешенности вала F₀ = 4,5 Н при угловой скорости 1 рад/с. Определить наибольшую вертикальную возмущающую силу, передаваемую фундаменту.

Решение

Ж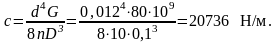 ёсткость одной пружины равна

Эквивалентная жёсткость 4-х параллельных пружин равна c_экв = 4·c = 82944 Н/м.

Квадрат угловой частоты свободных колебаний составляет ω_с² = с/m = 1843,2 с^–2. Круговая частота вынужденных колебаний ω_в= πn/30 = 188,5 с^-2.

Тогда центробежная сила, соответствующая этой частоте равна F = F₀· ω_в = 4,5·188,5 = 848,25 Н.

Используя уравнение (2.85), и учитывая, что коэффициент демпфирования 𝜀 = 0, получим коэффициент передачи силы

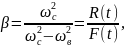
где R(t) – сила динамического воздействия на фундамент.

Откуда

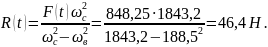
Пример 2.4

Тело, колеблющееся с вязким сопротивлением (рис. 2.13), совершает 10 полных колебаний в секунду. При этом амплитуда колебаний уменьшилась до 0,9 начальной амплитуды за 10 с.

Определить:

1. Коэффициент демпфирования ε.

2. Уменьшение периода колебаний, которое получится, если устранить затухание.

3. Логарифмический декремент колебаний δ.

Решение

1. Предположим, что движение описывается уравнением

Частота затухающих колебаний ω_з определится как ω_з = 2π·f = 20π.

Подставим в это уравнение х = 0,9·х₀, t = 10 с, ω_з = 20π, находим:

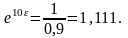
Откуда ε = 0,01054.

2. По определению ω_з² = ω_с² – ε², или ω_с² = ω_з² + ε². Вычислим

ω_с² = 3947,8418 с^-1.

Период затухающих колебаний

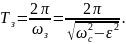
Период свободных колебаний без затухания Т_с = 2π/ω_с.

Отношение

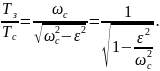
После вычислений, получаем Т_з /Т_с = 0,99999998.

3. Логарифмический декремент затухания по определению равен δ = ln∆ = ε· Т_з = 0,01054·1/10 = 0,001054.

Пример 2.5

Дано: одномассовая система с затуханием (рис. 2.13). Система выведена из состояния равновесия и совершает свободные колебания. Начальные условия: начальное смещение s = S₀, начальная скорость ṡ = 0, затухание больше критического, т.е. ε > ω_с.

Определить общий характер графической зависимости перемещение массы по времени.

Решение

Подставляя начальные условия s = S₀ и ṡ = 0 при t = 0 в выражение (2,44, а) и его первую производную по времени, находим:

С₁ + С₂ = s₀; C₁λ₁ + C₂λ₂ = 0, откуда

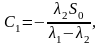
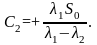
Таким образом, в этом случае общее решение принимает вид:

(2П.3)

Дважды дифференцируя это выражение по времени, находим следующие выражения для скорости и ускорения:

(2П.4)

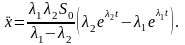(2П.5)

анализом выражения (2П.4) выявлено, что при t=0 и при t = ∞ скорость равна нулю и что она отрицательна для всех промежуточных значений t, так как обе величины λ₁ и λ₂ отрицательны. Чтобы найти момент t₁, в котором эта отрицательная скорость максимальна, приравняем выражение (2П.5) нулю и получим:

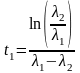(2П.6)

Из выражений (2П.3…2П.6) заключаем, что кривая «перемещение – время» имеет вид, показанный на рис. 2П.4.

Пример 2.6

Система, показанная на рис. 2П.5, подвергается действию вертикальной возмущающей силы F(t), которая изменяется во времени соответственно графику, изображённому на этом же рисунке. Пренебрегая демпфированием, найти установившийся процесс вынужденных колебаний x = f(t), если масса m и коэффициент жёсткости пружины с_пр таковы, что ω_в/ω_с = 0,9.

Решение

Разложим функцию F(t) в ряд Фурье:

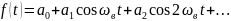
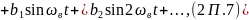
где ω_в = 2π/Т_в – круговая частота возмущающей силы.

Или можно записать

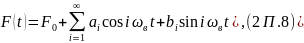
где

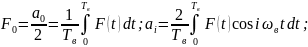
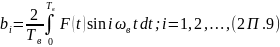
или в амплитудной форме

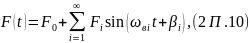
где

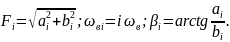
Рассматривая сначала выражение (2П.9), мы видим, что 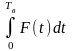есть просто площадь, ограниченная пилообразным графиком на рис. 2П.5, в интервале от t = 0 до t = 2 . Ясно, что эта площадь равна нулю, и поэтому a₀ = 0.

Рассматривая далее выражение (2П.9) в отношение a_i, мы видим, что каждая ордината графика рис. 2П.5 должна быть умножена на cosiω_вt и проинтегрирована в пределах от t = 0 до t = 2πω_в. Из антисимметрии функции F(t) относительно прямой t = πω_в и симметрии функции cosiω_вt относительно той же прямой заключаем, что этот интеграл исчезает и a_i = 0.

Рассматривая, наконец, выражение b_i, мы видим, что каждая ордината графика рис. 2П.5 должна быть умножена на siniω_вt и проинтегрирована в пределах от t = 0 до t = 2π/ω_в. В данном случае функция F(t), рассматриваемая в интервале от t = ш до t = π/ω_в симметрична относительно прямой t = π/2ω_в, а рассматриваемая в интервале от t = π/ω_в до t = 2π/ω_в, симметрична относительно прямой t = 3π/2ω_в.

Если i есть чётное число, то соответствующие участки функции siniω_вt антисимметричны относительно тех же прямых t = π/2ω_в и t = 3π/2ω_в . Таким образом, для i = 2,4,6,… мы получим b_i = 0.

Если i есть нечётное число, то функции F(t) и siniω_вt антисимметричны относительно прямой t = π/ω_в и получим:

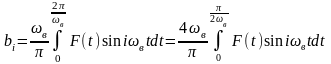. (2П.11)

Обращаясь к рис. 2П.5, мы видим, что в интервале от t = 0 до t = π/2ω_в

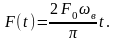
Подставляя это в выражение (2П.11), получаем:

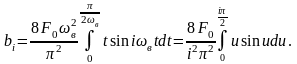
Интегрируя и подставляя пределы, находим:

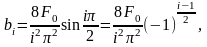(2П.12)

где, очевидно, i = 1,3,5,7,…

Учитывая, что a₀ = 0, a_i = 0 и используя выражение (2П.12) для b_i, получим ряд Фурье в виде:

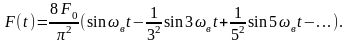(2П.13)

Как видно, для представления пилообразного графика на рис. 2П.5 виде тригонометрического ряда, мы должны суммировать синусоиды только с нечётным числом волн в интервале от t = 0 до t = 2π/ω_в. Это совершенно естественно, так как только в этом случае мы можем сохранить антисимметричную форму данного графика. Далее мы видим, что ряд (2П.13) сходится настолько быстро, что практически важен только первый член. Это попросту означает, что пилообразная возмущающая сила вызывает практически тот же эффект, что и простая гармоническая возмущающая сила несколько меньшей амплитуды:

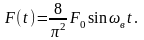(2П.14)

Чтобы оценить несущественность второго члена ряда, заметим, что при 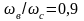коэффициент динамичности равен

.

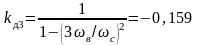Таким образом, амплитуда вынужденных колебаний, вызванных вторым членом ряда, равна всего 0,159/3²= 0,0177 от прогиба при статическом приложении силы 8F₀ /π². Коэффициент динамичности для первого члена ряда равен

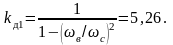
Следовательно, можно сделать вывод, не учёт второго члена ряда даёт ошибку, меньшую 0,4%. Приближенное выражение, описывающее перемещение, примет вид