1.2.1. Дифференциальные уравнения с разделяющимися переменными.
Уравнением с разделяющимися переменными (тип I) называются уравнения вида
,
,
.
Чтобы
решить уравнение типа I надо разделить
переменные, привести уравнение к виду
с разделенными переменными
и проинтегрировать почленно.
?
?
Как разделять переменные?
Для
отыскания решения уравнения
или
нужно разделить в нем переменные. Для
этого
заменим
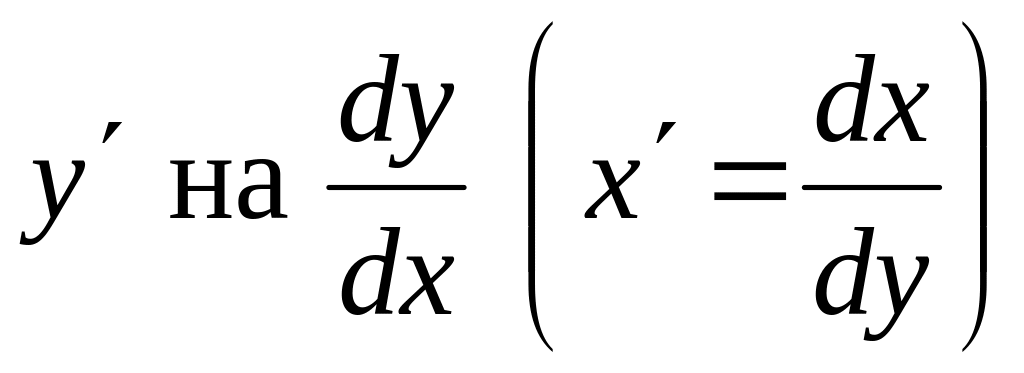,умножим обе части уравнения
(
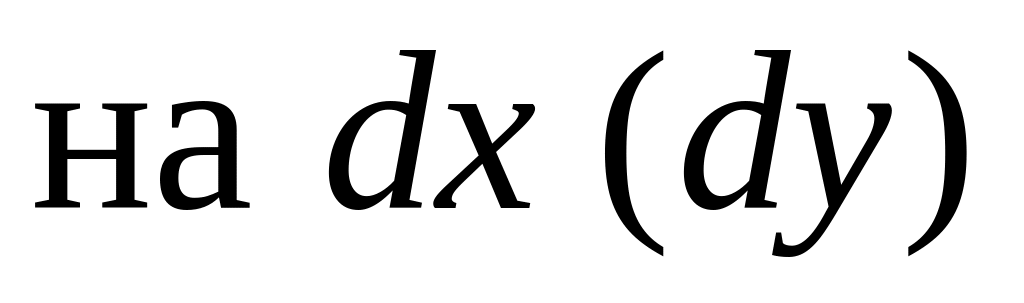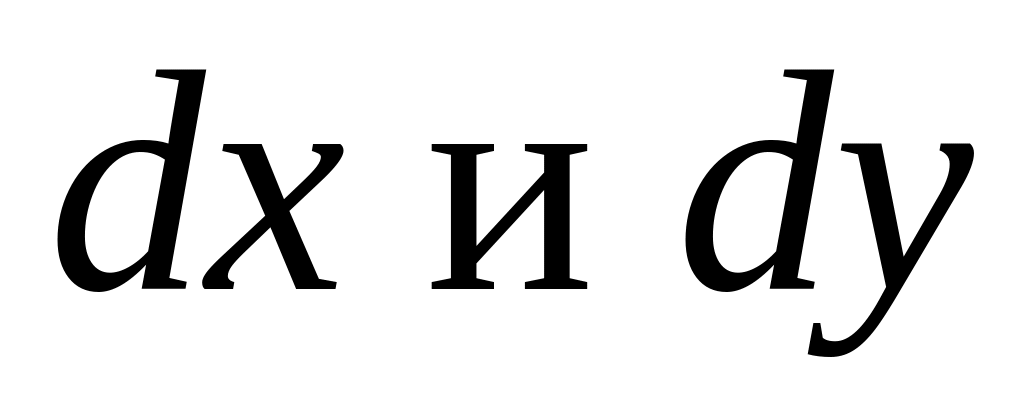должны быть только в
числителях),разделим обе части уравнения на такое выражение, чтобы в одну часть уравнения входило только , в другую – только , т. е.
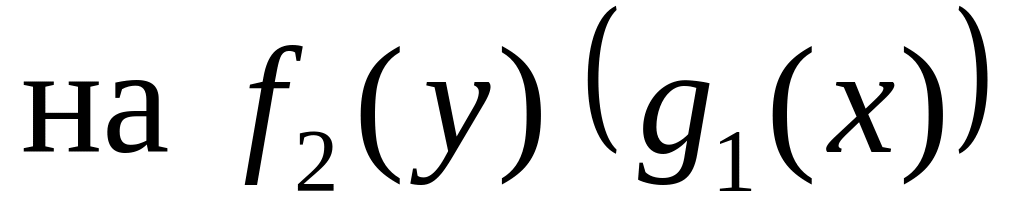,проинтегрируем обе части.
При делении обеих
частей уравнения на выражение, содержащее
неизвестные
,
могут быть потеряны решения (особые),
обращающие это выражение в нуль.
Пусть
дифференциальное уравнение задано в
дифференциальной форме (1.4). В частном
случае, когда каждая из функций
является произведением двух функций,
одна из которых – функция только
,
а вторая – только
,
т. е. когда
,
уравнение примет вид
.
Разделение
переменных производится делением обеих
частей полученного уравнения на
произведение
,
в котором
− функция только
,
являющаяся множителем
,
а
− функция только
,
являющаяся множителем
.
После деления на это произведение
уравнение примет вид
.
Это уравнение называется уравнением с разделенными переменными: находится функция, зависящая только , − только .
! !
Пример 2.1.1. Решить уравнение с
разделяющимися переменными
.
▲ 1.
2.
,
3.
.
▼
? ?
Для успешного усвоения темы необходимо
Уметь: 1. интегрировать, поэтому таблицу основных интегралов надо знать на память;
2. потенцировать любое выражение →
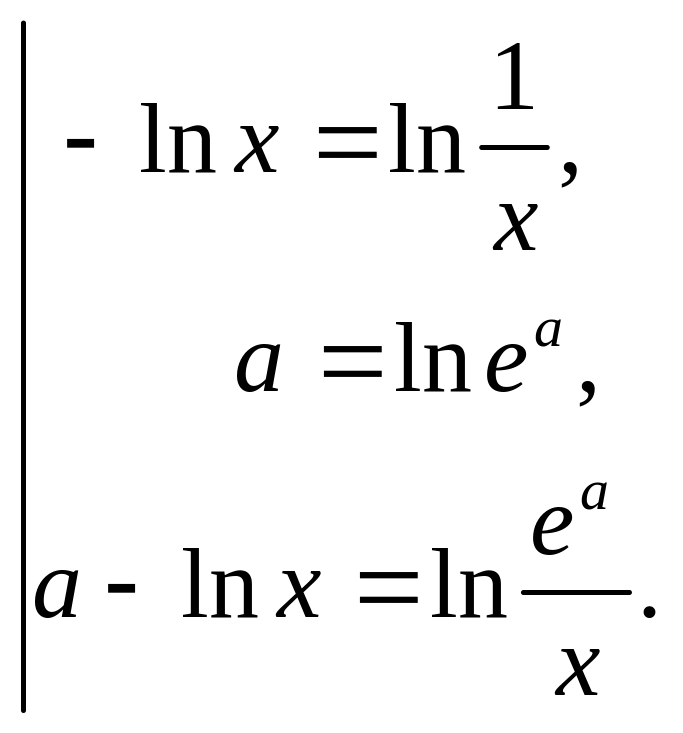
Помнить признаки дифференциальных уравнения с разделяющимися переменными и метод их решения.
Понимать смысл всех употребляемых терминов, понятий и символов.
Если Вы усвоили смысл термина
«произвольная постоянная», то Вам должно
быть понятно, что:
и то, что произвольную постоянную можно
писать в любой части равенства.
! !
Пример. 2.1.2. Найти частное решение
уравнения
,
удовлетворяющее начальным условиям
.
▲ 1.
,
2.
,
.
3.
.
,
.
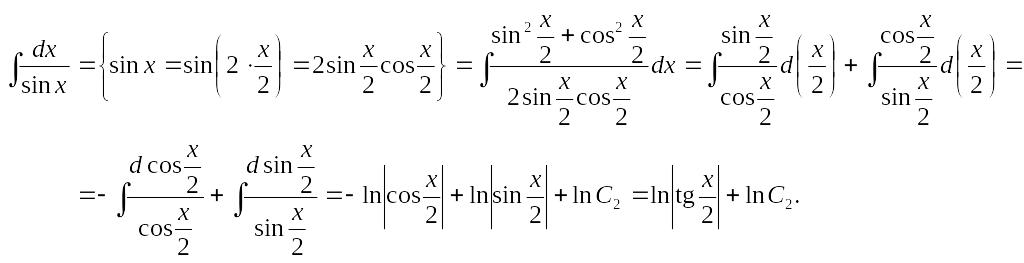
Обратите внимание, как записана
произвольная постоянная.
После потенцирования получаем общий
интеграл:
.
При отыскании частного решения к указанному выше алгоритму добавляется еще одна новая операция:
Найти , подставив в общее решение (интеграл) начальные условия, и записать частное решение.
4.
.
Частный интеграл:
.
1.2.2.
Однородные дифференциальные уравнении
(тип
)
Функция
называется однородной
функцией измерения
относительно аргументов
,
если равенство
справедливо
для любого
,
при котором функция
определена,
.
Дифференциальное
уравнение в нормальной форме
называется однородным
относительно переменных
,
если
− однородная функция нулевого измерения
относительно своих аргументов, т. е.
.
Однородное
дифференциальное уравнение в нормальной
форме всегда можно записать в виде
(положив
)
.
Уравнение в дифференциальной форме называется однородным, если функции − однородные функции одного измерения.
Однородное
уравнение с помощью замены
сводится к уравнению с разделяющимися
переменными относительно
и новой функции
.
? ?
Чтобы решить однородное уравнение, нужно:
Ввести подстановку
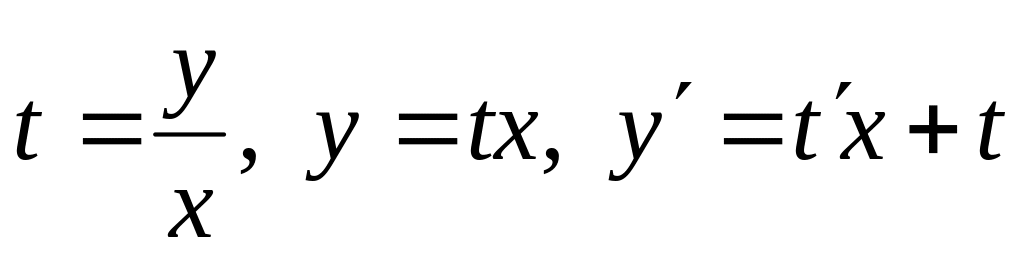сводится к уравнению типа
.Разделить переменные и проинтегрировать уравнение типа .
Результат интегрирования упростить, пропотенцировать, если нужно, и записать общий интеграл, вернувшись к исходной переменной.
! !
Пример
2.2.1. Решить уравнение
.
▲ Здесь
.
Имеем:
.
Следовательно,
− однородная функция нулевого измерения,
потому уравнение является однородным.
1.
− уравнение типа
.
2.
;
;
.
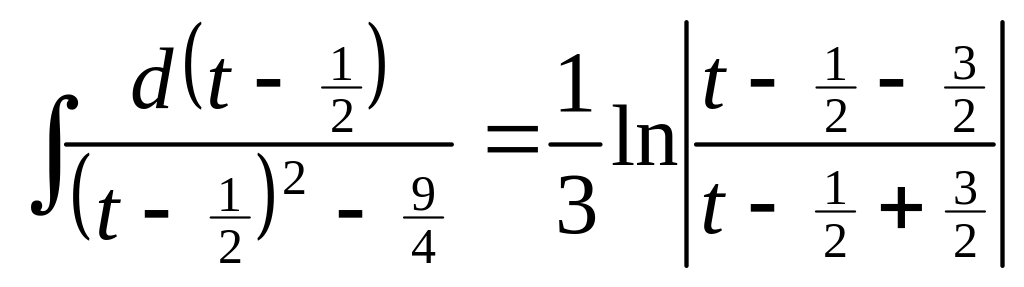В однородных уравнениях
лучше
относить
.
3. Общий интеграл
.
▼
Пример 2.2.2. Найти решение уравнения
.
▲ Коэффициенты
соответственно равны:
.
Функции
являются однородными функциями первого
измерения. Действительно,
,
.
Поэтому исходное уравнение является
однородным. Приведем уравнение к
нормальному виду, разделив его
.
Имеем
.
1.
− уравнение типа
.
2.
.
.
3. Общий интеграл
.
▼
Пример 2.2.3. Найти частное решение
уравнения
,
если
.
▲ Преобразуем уравнение
к нормальному виду:
.
Здесь
.
Имеем:
Следовательно, − однородная функция нулевого измерения, потому уравнение является однородным.
1.
− уравнение типа
.
2.
.
3.
.
Общий интеграл
.
4. Найдем
.
.
Частный интеграл
.
▼