8Формула Тейлора для функций нескольких переменных.

Пусть функция z=f(x,y) непрерывна вместе со своими частными производными до 3-его порядка включительно в некоторой окресности содержащей точку М(x0,y0,z0) Попытаемся представить эту фун-ию в виде многочлена второй степени по степеням x-x0, y-y0, этот многочлен имеет вид: f(x,y)=A0+B1(x-x0)+C1(y-y0)+(1/2!)( B2(x-x0)2+2C2(x-x0)(y-y0)+Д2(y-y0)2)+R2

Определим коэф А0, B1, C1, B2, C2, D2, коэф будем определять из условий, что функция и многочлен и их частные производные совпадают в точке (х0,у0). Найдем f(x0,y0)=А0

∂f/∂х=B1+(1/2)B2(x-x0) ∂f(x0,y0)/∂х=B1

∂f/∂у=C1+(1/2)2C2(x-x0) ∂f(x0,y0)/∂у=C1

продиференцировав еще раз мы получим, что

B2=∂2f(x0,y0)/∂x2 C2=∂2f(x0,y0)/∂x∂y D2=∂2f(x0,y0)/∂y2

Подставив найденные коэфициенты в формулу мы получим формулу Тейлора 2-ого порядка для функции z=f(x,y) в окрестности точки (x0,y0), она примет вид f(x,y)= f(x0,y0)+(∂f(x0,y0)/∂х)(x-x0)+

+(∂f(x0,y0)/∂у)(y-y0)+(1/2!)((∂2f(x0,y0)/∂x2)(x-x0)2+2(∂2f(x0,y0)/∂x∂y)(x-x0)(y-y0)+(∂2f(x0,y0)/∂y2)(y-y0)2)+R2.

9Условный экстремум функции нескольких переменных

Определение 1. Функция u=f(x1, ..., xm) имеет условный максимум (условный минимум) в точке 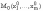, если существует такая окрестность U(M0) точки М0, что для всех точек M(x1, ..., xm) этой окрестности, удовлетворяющих уравнениям связи

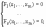
выполняется неравенство f(M0) f(M) (f(M0) f(M)).

То, что условный экстремум не совпадает, вообще говоря, с обычным экстремумом функции видно на следующем примере.

Пример 1. u = x2 + y2 при условии x+y-1=0

Безусловный экстремум этой функции достигается в точке (0,0) и равен 0.

Условный экстремум ищем при условии x+y-1=0, т.е. для функции

u = x2 + y2 = x2 + (1-x)2 = 2x2 - 2x + 1

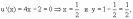
, поэтому в т. локальный минимум.

Следовательно функция u = x2 + y2 имеет условный минимум в т. (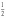 ; ), который равен .

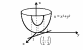
Задача нахождения условного экстремума сводится к исследованию на обычный экстремум функции Лагранжа

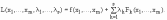
Параметры - называются множителями Лагранжа.

Необходимые условия условного экстремума записываются в виде системы

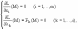
из которой находятся 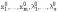, где 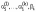- координаты точки, в которой возможен условный экстремум (для каждой такой точки получается свой (!) набор параметров ).

Достаточным условием условного экстремума является знакоопределенность второго дифференциала функции L при , вычисленного в точке . При этом требуется знакоопределенность второго дифференциала не для произвольных наборов dx1,...,dxm, а для наборов, связанных соотношениями: 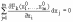(k = 1,2, ..., s).

(Эти соотношения получаются, если взять дифференциалы от уравнений связи).

10Определение вероятности

Вероятность события численно характеризует степень возможности его появления в рассматриваемом опыте.

Пусть производится опыт с n равнозначными исходами, образующими полную группу несовместных событий. Такие исходы называются элементарными исходами (событиями), случаями, шансами. Случай, который приводит к наступлению события А, называется благоприятным (или благоприятствующим) ему.

Вероятностью события А называется отношение числа m случаев, благоприятствующих этому событию, к общему числу n случаев.

p(A)=m/n

Такое определение вероятности называется классическим определение вероятности.

Из классического определения следуют свойства вероятности:

0≤p(A)≤1

p(Ø)=0,

p(Ω)=1,

p(Ā)=1-p(A)

p(A+B)= p(A)+ p(B), если AB=Ø

Теорема сложения и теорема умножения вероятностей

ОПРЕДЕЛЕНИЕ. Суммой А+В двух событий А и В называют событие, состоящее в появлении события А, или события В, или обоих этих событий.

Например, если из орудия произведены два выстрела и А – попадание при первом выстреле, В – попадание при втором выстреле, то событие А+В – попадание хотя бы при одном выстреле (или при первом выстреле, или при втором, или в обоих случаях).

Теорема 1.(теорема сложения вероятностей)

Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

P(A+B)=P(A)+P(B) (3)

Доказательство: Введем обозначения: n – общее число возможных элементарных исходов испытания; m1 – число исходов, благоприятствующих событию А; m2 – число исходов, благоприятствующих событию В.Число элементарных исходов, благоприятствующих наступлению либо события А, либо события В, равно m1+m2. Следовательно, P(A+B)=(m1+m2)/n=. Приняв во внимание, что m1/n=P(A) и m2/n=P(B), окончательно получим P(A+B)=P(A)+P(B)

Следствие 1. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

P(A1+A2+...+An)=P(A1)+P(A2)+...+P(An)

Теорема 4. (теорема умножения вероятностей) Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:

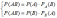
Следствие 2. Эту теорему можно обобщить на любое конечное число зависимых событий A1,A2,...,Ak

P(A1,A2,...,Ak)=P(A1)•PA1(A2)•PA1A2(A3)...PA1A2...Ak-1(A)

Событие В называют независимым от события А, если появление события А не изменяет вероятности события В, т.е. если условная вероятность события В равна его безусловной вероятности PAB=P(B)