1 Предел и непрерывность функций нескольких переменных

Пусть функция определена по области Dплоскости

О: Число, в случае когда для любого числа существует такое число, что для всех т. кроме, быть может т. , верно неравенство

Главные теоремы о пределах функции одной переменной (см. разд. 7.5) верны и для функций двух и большего числа переменных.

О: Функция именуется непрерывной в т., если: 1) она определена в т 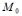.и её окрестности, 2) .

О: Функция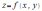 именуется непрерывной на некотором множестве , когда она является непрерывной в любой точке этого множества.

О: Точка именуется точкой разрыва функции , когда для неё неверно хотя бы одно условие 1), 2). Точки разрыва могут являться изолированными, а также формировать линии разрыва.

Примеры: 1) .

◄Функция не определена в тех точках, где знаменатель становится нулём — линия разрыва ►

◄ т. — точка разрыва ►

В случае трёх и более переменных определения предела и непрерывности остаются подобными приведённым.

О: Число A называется пределом функции существует такое, что из условия следует

2Частные производные функции нескольких переменных

Пусть М(х1, х2, ..., хm) внутренняя точка области определения функции u=f(x1, ..., xm). Пусть xk - приращение k-ой координаты в данной фиксированной т.М, ему соответствует частное приращение функции

xku f(x1, ..., xk-1, xk + xk, xk+1, ..., xm) - f(x1, ..., xm).

Рассмотрим отношение , которое зависит от xk и определено при всех достаточно малых xk, отличных от нуля.

Определение 1. Если существует , то он называется частной производной функции u=f(x1, ..., xm) в т. М(x1, ..., xm) по аргументу xk и обозначается одним из символов: . Таким образом, .

Замечание. Так как изменяется только xk + xk, т.е. k-я координата аргумента функции f, то частная производная является обыкновенной производной функции f как функции только k-й переменной (при фиксированных остальных переменных). Это позволяет вычислить частные производные по одной из переменных по обычным формулам дифференцирования, если зафиксировать все остальные переменные.

Пример 1. u = x2 + 3xy - y

вычисляем при условии, что y = const

вычисляем при условии, что x = const

Выясним теперь, насколько полную информацию дают частные производные функции в данной точке о поведении функции в окрестности этой точки.

Сразу отметим, что частные производные в т.М0 могут дать информацию о поведении функции только на прямых, проходящих через т.М0 и параллельных координатным осям.

Конечно, этой информации совсем не достаточно, чтобы судить о поведении функции в целой окрестности т.М0 (и, в частности, на других лучах, проходящих через т.М0).

Пример 3. Функции показывает, что частные производные ее

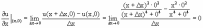
(аналогично )

существуют и обращаются в нуль не только в т. (0,0), но и всюду на координатных осях, а сама функция не имеет в т. (0,0) предела (см. тему 4). Заметим, что в одномерном случае из существования производной следовала непрерывность функции.

Таким образом, мы приходим к необходимости ввести более сильное условие, чем существование частных производных, чтобы оно было аналогом дифференцируемости функции одной переменной. Это условие должно быть связано с полным приращением функции в точке.