16.1.3. Локальная суперсимметрия

Лагранжиан Li + L₂ при а = ±¹А(яа^/)-¹ обладает замечатель­ными свойствами. Он не только инвариантен при двумерных преобразованиях координат, но также обладает локальной сим­метрией нового типа [56]. Эта симметрия связана с произволь­ными функциями, являющимися одновременно d-мерными спи­норами и 2-мерными векторами.

Для ее описания удобно ввести проекционные операторы

(16.1.3.1)

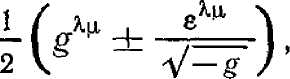
которые проектируют двумерный вектор v^k на его изотропные компоненты t>^_:

(16.1.3.2)

Суперструна 245

где знаки ± относятся к двум измерениям. Операторы P_±[ii

удовлетворяют соотношениям

^ (16.1.3.3а)

-v, (16.1.3.36)

~^P% = 0, (16.1.3.Зв)

^ (16.1.3.3г)

и не столь очевидному тождеству

Р%Р% = P5:^PPi°. (16.1.3.4)

Если; двумерный вектор удовлетворяет условию и^Л—о^_, то

он касателен к одному из изотропных направлений ').

Локальные преобразования суперсимметрии, относительно которых действие инвариантно, имеют следующий явный вид:

(16.1.3.5а) ^_А^ (16.1.3.56)

= i (§ V^¹ + §V^e²), (16. 1.3.5b)

= -16 У^ (Р^код^ + р>Г^а_Ре²),

(16.1.3.5г)

где х¹ и я² — инфинитезимальные параметры²). Как отмеча­лось выше, эти параметры представляют собой двумерные век­торы и чисто мнимые десятимерные спиноры с киральностью, противоположной той, которую имеют 8¹ или G² (так что 6_KG^a имеет ту же киральность, что и 8^а).

Из системы (16.1.3.5) можно видеть, что в законы преобра­зования входят только спроецированные компоненты %^{^ и х²^.

Кроме того, поскольку двумерные изотропные компоненты со^ определяют десятимерные изотропные векторы

= 0 (16.1.3.6)

л ft

¹) Если k n n — два ненулевых изотропных вектора, удовлетворяющих условиям kr = k₊ и п ■=■ п_ (=4- k k^ = п п^ = 0 и k п^ Ф 0 обычно норми -

руется на минус единицу), то легко видеть, что v^ = v\-\-v^_, v^_ = v₊k и v_ — v_n , где v₊ и v_ — компоненты с в изотропной системе отсчета

²) Нет нужды выписывать вариацию g^ , поскольку в действие входит только унимодулярная комбинация V— §" g"^¹¹-

246 Глава 16

в результате полевых уравнений для метрики (см. следующий раздел), матрицы а>^у_А необратимы (они нильпотентны). Та­ким образом, в соотношениях (16.1.3.5а) — (16.1.3.5в) содержит­ся дополнительное проецирование пространственно-временных спиноров %¹} и %²£ на одну из их изотропных спинорных компо­нент. Поэтому количество действительных калибровочных па­раметров в этих соотношениях равно 2X8=16 (8—количе­ство компонент изотропного кирального спинора). Это верно также для преобразования (16.3.3.5г), если принять во внима­ние спинорные уравнения движения.

Для проверки инвариантности действия S\ + S₂ (в котором а = ¹/₂(па^/)~¹)— объекта преобразований (16.1.3.5), заметим, что если вариация Ь_КХ^А связана с 6_КВ^: и 6_ИВ² посредством урав­нения (36.1.3.5b), to вариация действия дается выражением

_{б (V-}

_9?

-Ш \

_ik

_{kr \ «Ы» V}

jjj \ ^ 682, (16.1.3.7)

где мы проинтегрировали по частям, чтобы исключить произ­водные от S8¹ и 68² (заметим, что они сокращаются в £)

Если теперь к членам д^удд^¹ и дя9²улдй6² применить пре­образование Фирца с помощью тождества (16.1.2.5), то в ре­зультате получим

1 Г / / 1 л

4яа' J ^ S ё ) х А\х

% Г / /„1*я1 д,л! , _л,ля2 ^А$}ъ_Аш (16.1.3.8)

яа

Дальнейшее использование уравнений (16.1.3.5) и (16.1.3.4) приводит к искомому результату 65 = 0.

Поскольку параметры калибровочных преобразований анти-коммутируют, данные преобразования можно называть "локаль-

Суперструна 247

ными суперсимметриями". Следует, однако, помнить, что эти параметры являются двумерными векторами. Новые калибро­вочные преобразования не вполне поняты (об этом подробнее см. ниже), неясно также их отношение к двумерной супергра­витации¹). Это является, вероятно, одной из причин того, что ковариантное квантование суперструны до сих пор не прове­дено до конца.

Добавочная калибровочная инвариантность дает достаточно -свободы для фиксации калибровки, в которой теория может быть полностью разрешена как на классическом, так и на кван­товом уровне. Без этой калибровочной инвариантности о кван­товой теории, по-видимому, ничего нельзя сказать, так что мы отвергаем случаи а ф —]/2па^/2) из соображений простоты.

Таким образом, окончательно ковариантное действие супер­струны имеет вид

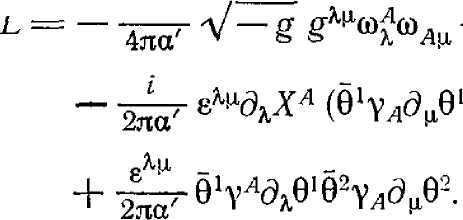(16.1.3.9) Это действие найдено Грином и Шварцем [56].