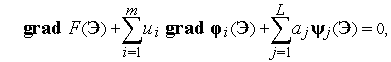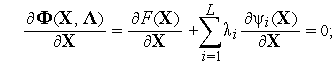Необходимые условия экстремума

В задачах безусловной оптимизации необходимые условия представляют собой равенство нулю градиента целевой функции

В общей задаче математического программирования необходимые условия экстремума, называемые условиями Куна-Таккера, формулируются следующим образом:

Для того чтобы точка   была экстремальной точкой выпуклой задачи математического программирования, необходимо наличие неотрицательных коэффициентов  , таких, что

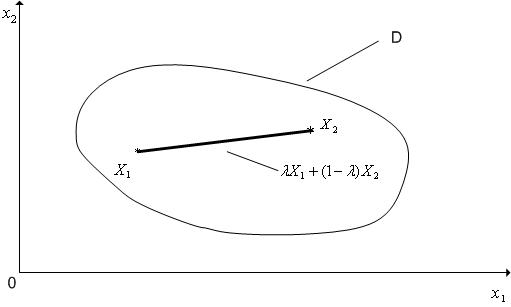 выпуклое множества (n=2).

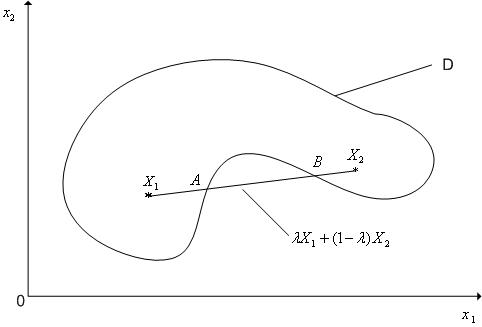не выпуклое множество (n=2).

(1)

и при этом соблюдались ограничения задачи, а также выполнялось условие

(2)

где   — число ограничений типа неравенств (множество допустимых значений вектора варьируемых параметров формируется только ограничениями типа неравенств),   — то же для равенств, коэффициенты  .

Если максимум находится внутри допустимой области  , то, выбирая все  , добиваемся выполнения (1);

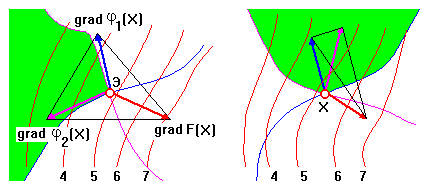
- если же точка максимума   лежит на границе области  , то, как видно из левой части рис. 1, эту точку всегда соответствующим подбором неотрицательных   можно поместить внутрь оболочки, натянутой на градиенты целевой функции   и функций-ограничений  .

- наоборот, если точка не является экстремальной, то (1) нельзя выполнить при любом выборе положительных коэффициентов   (см. правую часть рис. 9, где рассматриваемая точка   лежит вне выпуклой оболочки, натянутой на градиенты).

Теорема означает, что в ее условиях вместо задачи условной оптимизации, можно решать задачу безусловной оптимизации.

Необходимым условием существования локального минимума этой задачи в некоторой точке  является условие (2).

Рис. 9.  Пояснение условий Куна-Таккера

Методы поиска условных экстремумов

Метод множителей Лагранжа, ориентирован на поиск экстремума при наличии ограничений типа равенств  , т.е. на решение задачи

(1)

где  .

Суть метода заключается в преобразовании задачи условной оптимизации (1) в задачу безусловной оптимизации с помощью образования новой целевой функции где  — вектор множителей Лагранжа,   — число ограничений. Необходимые условия экстремума функции  :

(2)

Система (2) содержит   алгебраических уравнений, где   — размерность пространства управляемых параметров, ее решение дает искомые координаты экстремальной точки и значения множителей Лагранжа. Однако при численном решении (2), что имеет место при использовании алгоритмических моделей, возникают те же трудности, что и в методе Ньютона. Поэтому в САПР основными методами решения задач математического программирования (ЗМП) являются методы штрафных функций и проекции градиента.

Основная идея методов штрафных функций — преобразование задачи условной оптимизации в задачу безусловной оптимизации путем формирования новой целевой функции   введением в исходную целевую функцию   специальным образом выбранной функции штрафа  : где   — множитель, значения которого можно изменять в процессе оптимизации.

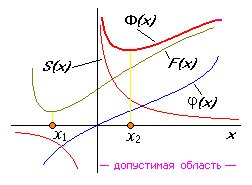
Функция штрафа обеспечивает появления барьера у целевой функции   и соотношение между условным в точке   и безусловным в точке   минимумами   . Штрафная функция не единственна. Обычно она стремится в бесконечности в точках, где ограничения не выполняются и равно 0 во всех остальных точках. В одномерном случае ситуация иллюстрируется рис. 10.

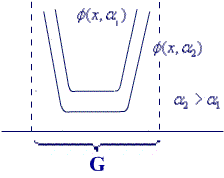
Функция   называется штрафной функцией множества G, если  для любых параметров     

Таким образом, задача условной минимизации f (x) заменяется последовательностью задач безусловной минимизации   при k =1,2,.... При этом, исходя из заданной начальной точки x0, находится последовательность точек   сходящаяся при определенных условиях к решению  исходной задачи. В зависимости от вида Ф(х, а) различают методы внешних штрафных функций и методы внутренних штрафных функций или барьерных функций.

На рис.- внутренние щтрафные функции.

Рис. 10.  Метод штрафных функций

Основной вариант метода проекции градиента ориентирован на задачи математического программирования c ограничениями типа равенств.

Поиск при выполнении ограничений осуществляется в подпространстве   измерений, где   — число управляемых параметров,   — число ограничений, при этом движение осуществляется в направлении проекции градиента целевой функции   на гиперплоскость, касательную к гиперповерхности ограничений (точнее к гиперповерхности пересечения гиперповерхностей ограничений).

Поиск минимума начинают со спуска из исходной точки на гиперповерхность ограничений. Далее выполняют шаг в указанном выше направлении (шаг вдоль гиперповерхности ограничений). Поскольку этот шаг может привести к заметному нарушению ограничений, вновь повторяют спуск на гиперповерхность ограничений и т.д. Другими словами, поиск заключается в выполнении пар шагов, каждая пара включает спуск на гиперповерхность ограничений и движение вдоль гиперповерхности ограничений.

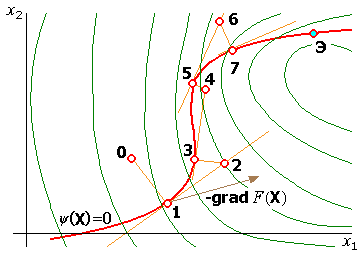
Идею метода легко пояснить для случая поиска в двумерном пространстве при одном ограничении  . На рис. 11 это ограничение представлено жирной линией, а целевая функция — совокупностью более тонких линий равного уровня. Спуск обычно осуществляют по нормали к гиперповерхности ограничений (в данном случае к линии ограничения). Условие окончания поиска основано на сопоставлении значений целевой функции в двух последовательных точках, получаемых после спуска на гиперповерхность ограничений.

Рис. 11.  Траектория поиска в соответствии с методом проекции градиента

Недостаток всех градиентных методов в том, что гарантии определения глобального экстремума нет.

Пакеты прикладных программ оптимизации присутствуют во всех САПР, CALS и CASE системах. Например, в MATHLAB их вид следующий:

X = f min con (fun, x0, A, B) - простейший вариант, ищет минимум скалярной функции fun на интервале А, В и представлении А X меньше = В

X = f min con (fun, x0, A, B, ограничения 1, ограничения 2) – в том числе для существующих градиентов, ограничений, матрицы вторых производных Г.

И т.д. по мере усложнения

Экспериментальное тестирование алгоритмов оптимизации

В качестве критерия качества алгоритма оптимизации   обычно рассматривают затраты времени на поиск. Эти затраты складываются из затрат на испытания и из затрат на нахождение точек   по информации о предыдущих испытаниях (можно сказать – из затрат на вычисления значений функции  ). Поскольку в задачах САПР последние затраты много меньше первых, в качестве критерия качества алгоритма оптимизации A можно использовать

количество испытаний  , необходимых для нахождения минимума функции   с заданной точностью   при начальном приближении  .

Для корректного сравнения эффективности различных алгоритмов, экспериментальное тестирование алгоритмов оптимизации необходимо выполнять при одинаковых значениях заданной точности решения  . Поэтому будем в качестве критерия качества алгоритма оптимизации   на классе функций { ( )} использовать критерий  .

При заданной точности решения эффективность любого алгоритма поисковой оптимизации зависит от начального приближения   .

Точность решения задачи оптимизации определяется используемым условием окончания поиска.

Подходы к решению задач структурного синтеза

Задачи синтеза структур проектируемых объектов относятся к наиболее трудно формализуемым. Существует ряд общих подходов к постановке этих задач, однако практическая реализация большинства из них неочевидна. Структурный синтез, как правило, выполняют в интерактивном режиме при решающей роли инженера-разработчика, а ЭВМ играет вспомогательную роль: предоставление необходимых справочных данных, фиксация и оценка промежуточных и окончательных результатов.

Задачу принятия решений (ЗПР) формулируют следующим образом:

где   — множество альтернатив проектного решения (морфологическое множество),   — множество критериев (выходных параметров), по которым оценивается соответствие альтернативы поставленным целям;  — модель, позволяющая для каждой альтернативы рассчитать вектор критериев при условии ,   — решающее правило для выбора наиболее подходящей альтернативы в многокритериальной ситуации.

Простейший способ задания множества   — явное перечисление всех альтернатив. Каждой альтернативе в информационно-поисковой системе ИПС соответствует поисковый образ, состоящий из значений атрибутов   и ключевых слов вербальных характеристик.

Явное перечисление альтернатив при представлении множества альтернатив возможно лишь при малой мощности  . Поэтому в большинстве случаев используют неявное описание   в виде способа (алгоритма или набора правил  ) синтеза проектных решений из ограниченного набора элементов  . Поэтому здесь  , а типичный процесс синтеза проектных решений состоит из следующих этапов:

1. формирование альтернативы   (это может быть выбор из базы данных ИПС по сформированному поисковому предписанию или генерация из   в соответствии с правилами  );

2. оценка альтернативы по результатам моделирования с помощью модели ;

3. принятие решения относительно перехода к следующей альтернативе или прекращения поиска (выполняется лицом, принимающим решение или автоматически).

Для описания множеств набора правил    и набора элементов   используют следующие подходы.

• морфологические таблицы и альтернативные И-ИЛИ-деревья;

• представление знаний в интеллектуальных системах — фреймы, семантические сети, продукции;

• генетические методы;

• базы физических эффектов и эвристических приемов, применяемые при решении задач изобретательского характера.

Морфологическая таблица ( ) представляет собой обобщенную структуру в виде множества функций, выполняемых компонентами синтезируемых объектов рассматриваемого класса, и подмножеств способов их реализации. Каждой функции можно поставить в соответствие одну строку таблицы, каждому способу ее реализации — одну клетку в этой строке. Следовательно, в морфологических таблицах элемент   означает  -й вариант реализации  -й функции в классе технических объектов, описываемом матрицей  . Морфологические таблицы считают средством неавтоматизированного синтеза, помогающим человеку просматривать компактно представленные альтернативы, преодолевать психологическую инерцию. Последнее связано с тем, что внимание человека, принимающего решения обращается на варианты, которые без морфологической таблицы оставались бы вне его поля зрения.

Любую морфологическую таблицу можно представить в виде дерева. В общем случае разные функции могут быть реализованы одними и теми же способами, тогда вместо дерева имеем граф, называемый И-ИЛИ-графом (или альтернативным графом).

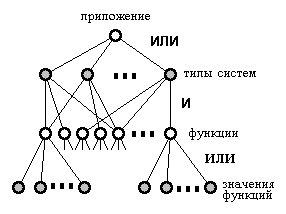
 Каждая И вершина дерева соответствует частной морфологической таблице, т.е. множеству функций так, что  -я выходящая ветвь отображает  -ю функцию. Каждая ИЛИ вершина, инцидентная  -й ветви, соответствует множеству вариантов реализации  -й функции, при этом  -я исходящая из ИЛИ вершины ветвь отображает  -й вариант реализации.

Трудности эффективного решения задачи существенно возрастают при наличии ограничений, типичными среди которых являются ограничения на совместимость способов реализации разных функций, т.е. ограничения вида

(1)

где  , если в оцениваемый вариант вошел элемент  , иначе  .

Условие (1) означает, что в допустимую структуру не могут входить одновременно элементы   и  . Совокупность ограничений типа (1) можно представить как систему логических уравнений с неизвестными  . Тогда задачу синтеза можно решать эволюционными методами, если предварительно или одновременно с ней решать систему логических уравнений (задачу о выполнимости).

Стремление к сокращению перебора решений, составляют операции разделения множества вариантов на подмножества и отсечения неперспективных подмножеств. Эти методы объединяются под названием метода ветвей и границ. Основная разновидность метода ветвей и границ относится к точным методам решения комбинаторных задач. Смысл метода в ветвлении множества М на подмножества, вычисление в каждом границ, например, нижних, сортировка подмножеств с наиболее интересными результатами и снова ветвление…

Сущность метода распространения ограничений заключается в сужении допустимых интервалов управляемых переменных   с помощью учета (распространения) исходных ограничений на выходные параметры   и  .

Для пояснения метода рассмотрим простой пример. Пусть в задаче фигурируют три управляемых целочисленных переменных  ,  ,  , заданы исходные интервалы допустимых значений этих переменных  ,  ,  , а область   определена ограничениями

(1)

(2)

Распространение ограничения (1) на интервал переменной   приводит к уменьшению его верхней границы, так как   , а с учетом ограничения (2) — к ее новой корректировке  , так как  , а также к увеличению нижних границ переменных   и  , так как решение неравенств   и (2) дает  ,  . Таким образом, получено сужение допустимой области  ,  ,  .

Метод легко распространяется на задачи с нечисловыми параметрами. В этом случае вместо сокращения числовых интервалов уменьшают мощности допустимых подмножеств значений параметров.

На базе метода распространения ограничений компанией ILOG создан программный комплекс оптимизации и синтеза проектных решений, состоящий из подсистем Solver, Configurator, Scheduler и др. Основной продукт - ILOG Solver. ILOG Solver поддерживает работу с целыми, вещественными, логическими и множественными переменными и позволяет использовать линейные, нелинейные и логические ограничения. В ILOG Solver реализовано несколько эффективных алгоритмов поиска, включающих как стандартные стратегии (поиск в глубину, поиск сначала наилучшего), так и специализированные алгоритмы для задач удовлетворения ограничения над конечными областями .