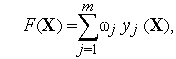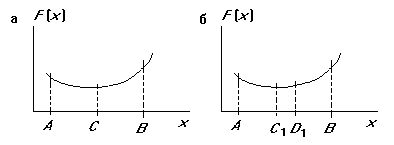Лекция 10. Критерии оптимальности

Наиболее эффективным способом исследования работоспособности сложного вычислительного/радиотехнического устройства является его моделирование. На сегодняшний день основными способами исследования работоспособности вычислительных устройств являются следующие: макетирование, физическое моделирование, аналитическое моделирование и математическое моделирование.

Натурное макетирование - один из наиболее старых способов проектирования РЭА. Его главное достоинство - максимальная достоверность результатов, обусловленная работой с реальными схемами, а не их приближенными моделями. Кроме того, макетирование характеризуется наглядностью получаемых результатов. В то же время макетирование имеет ряд крупных недостатков. Основные из них - высокая стоимость, длительность создания макета, ограничение возможности макетирования.

Физическое моделирование представляет собой исследование объектов одной физической природы с помощью объектов, имеющих другую физическую природу, но при этом одинаковое с исследуемыми объектами математическое описание. В основе физического моделирования лежит обычно принцип электрофизических аналогий. Он может применяться для изучения сопутствующих работе схем, например, тепловых процессов, математическое моделирование которых слишком сложно и трудоемко.

Аналитическое моделирование по заранее известным формулам или расчет по аналитическим выражениям выполняется с помощью формул, связывающих выходные параметры интегральных схем (функциональные и изменяемые) с внутренними параметрами, т.е. параметрами их отдельных компонентов. При этом делаются значительные упрощения. Например, экспоненциальные вольтамперные зависимости считаются линейными. Основные недостатки данного метода проектирования БИС - высокая трудоемкость вывода формул и, как правило, низкая точность расчетов. Основное достоинство - доступность.

Моделирования на компьютере предполагает использование в качестве объекта отладки программной модели проектируемой системы. Этот метод является универсальным в том смысле, что программная модель может быть получена для вычислительной системы любой структуры и архитектуры. Наиболее широко применяемым методом проектирования является математическое моделирование, под которым обычно понимается составление математической модели устройства и ее использованием на ЭВМ в процедурах расчета, анализа, оптимизации и синтеза.

Автоматизированное проектирование включает решение задач расчета, анализа, оптимизации и синтеза. Эти задачи называются проектными процедурами и имеют следующее содержание:

• расчет - определение выходных параметров и характеристик устройства при неизменных значениях его внутренних параметров и постоянной структуре;

• анализ - определение изменения выходных параметров и характеристик устройства в зависимости от изменения его внутренних и выходных параметров. В автоматизированном проектировании задача расчета часто называется одновариантным анализом, а задача синтеза - многовариантным анализом;

• оптимизация - определение наилучших в том или ином смысле значений выходных параметров и характеристик путем целенаправленного изменения внутренних параметров устройства. Это является содержанием параметрической оптимизации. Оптимизация структуры устройства является содержанием структурной оптимизации.

• В общем случае синтезом называется генерация исходного варианта устройства, включая его структуру при структурном синтезе и получение его внутренних параметров при параметрическом синтезе. Полученное в результате синтеза устройство не обязательно должно быть наилучшим, но обязательно работоспособным. В большинстве случаев устройство, полученное в результате синтеза, даже оптимального, требует доработки, чтобы удовлетворить многочисленным требованиям, учесть которые на стадии синтеза невозможно из-за их многообразия и сложности.

Реальный процесс автоматизированного проектирования РЭА обычно состоит из двух этапов:

1. Синтеза структуры и эскизного, обычно неавтоматизированного, по упрощенным формулам расчета ее параметров с целью получения работоспособного варианта РЭА, который будет играть роль начального приближения. Следует отметить, что в настоящее время ведутся работы по автоматизации и этого этапа проектирования.

2. Доводки полученного варианта до кондиций, соответствующих техническому заданию (ТЗ) с помощью оптимизации – параметрического синтеза.

Оптимизация как раздел математики существует достаточно давно. Оптимизация - это выбор, т.е. то, чем постоянно приходится заниматься в повседневной жизни. Термином "оптимизация" в литературе обозначают процесс или последовательность операций, позволяющих получить уточненное решение. Хотя конечной целью оптимизации является отыскание наилучшего или "оптимального" решения, обычно приходится довольствоваться улучшением известных решений, а не доведением их до совершенства. Поэтому под оптимизацией понимают скорее стремление к совершенству, которое, возможно, и не будет достигнуто.

Процедуры параметрического синтеза в САПР выполняются либо человеком в процессе многовариантного анализа (в интерактивном режиме), либо реализуются на базе формальных методов оптимизации (в автоматическом режиме). В последнем случае находят применение несколько постановок задач оптимизации.

А) детерминированная постановка: заданы условия работоспособности на выходные параметры   и нужно найти номинальные значения проектных параметров  , к которым относятся параметры всех или части элементов проектируемого объекта.

Б) стохастическая постановка - задача оптимизации, в которой критерий оптимальности  и/или ограничивающие функции  зависят от случайного вектора внешних параметров  . 

Проектные задачи являются многокритериальными, возникает проблема выбора критерия b сведения многокритериальной задачи к однокритериальной. Применяют несколько способов выбора критерия оптимальности. В частном критерии среди выходных параметров один выбирают в качестве целевой функции, а условия работоспособности остальных выходных параметров относят к ограничениям задачи (1).

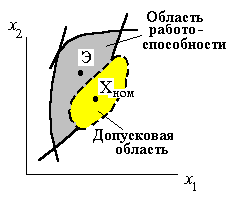
Рис. 1.  Области Парето и работоспособности

На этом рисунке представлено двумерное пространство выходных параметров   и  , для которых заданы условия работоспособности   и  . Кривая   является границей достижимых значений выходных параметров. Это ограничение объективное и связано с существующими физическими и технологическими условиями производства, называемыми условиями реализуемости. Область, в пределах которой выполняются все условия реализуемости и работоспособности, называют областью работоспособности. Множество точек пространства выходных параметров, из которых невозможно перемещение, приводящее к улучшению всех выходных параметров, называют областью компромиссов, или областью Парето. Участок кривой   (см. рис. 1) относится к области Парето.

Аддитивный критерий объединяет (свертывает) все выходные параметры (частные критерии) в одну целевую функцию, представляющую собой взвешенную сумму частных критериев

(2)

где   — весовой коэффициент,   — число выходных параметров. Функция (2) подлежит минимизации, при этом если условие работоспособности имеет вид   , то  .

Недостатки аддитивного критерия — субъективный подход к выбору весовых коэффициентов и неучет требований ТЗ.

Аналогичные недостатки присущи и мультипликативному критерию, целевая функция которого имеет вид

(3)

Нетрудно видеть, что если прологарифмировать (3), то мультипликативный критерий превращается в аддитивный.

Более предпочтительным является максиминный критерий, в качестве целевой функции которого принимают выходной параметр, наиболее неблагополучный с позиций выполнения условий работоспособности. Например, по всем параметрам имеется 50% запас, а по одному -10%. Расчет ведется по достижению максимума этого параметра, например 30% при допустимых запасах остальных параметров.

В математическом программировании базовая задача оптимизации ставится как задача  определение экстремума

где   — целевая функция,   — вектор управляемых (проектных) параметров,   и   — функции-ограничения,   — допустимая область в пространстве управляемых параметров.

(1)

Запись (1) интерпретируется как задача поиска экстремума целевой функции путем варьирования управляемых параметров в пределах допустимой области.

Таким образом, для выполнения расчета номинальных значений параметров необходимо, во-первых, сформулировать задачу в виде (1), во-вторых, решить задачу поиска экстремума 

Задачи оптимизации с учетом допусков

Если проектируются изделия для дальнейшего серийного производства, то важное значение приобретает такой показатель, как процент выпуска годных изделий в процессе производства. Очевидно, что успешное выполнение условий работоспособности в номинальном режиме не гарантирует их выполнения при учете производственных погрешностей, задаваемых допусками параметров элементов. Поэтому целью оптимизации становится максимизация процента выхода годных, а к результатам решения задачи оптимизации относятся не только номинальные значения проектных параметров, но и их допуски.

На рис. 2 представлены области работоспособности и область допусков в двумерном пространстве управляемых параметров. Обычно допуски заданы и не относятся к управляемым параметрам, поэтому цель оптимизации — максимальным образом совместить эти области, чтобы вероятность выхода за пределы работоспособности была минимальной.

Допустим, что оптимизация достигается при совмещении центров областей работоспособности   и допусковой  и сводится к задаче центрирования, т.е. к определению центра  .

Рис. 2.  Допусковая область и область работоспособности

Классификация методов математического программирования

Основными методами оптимизации в САПР являются поисковые методы. Поисковые методы основаны на пошаговом изменении управляемых параметров где в большинстве методов приращение   вектора управляемых параметров вычисляется по формуле

(1)

Здесь   — значение вектора управляемых параметров на  -м шаге;   — шаг; а   — направление поиска. Следовательно, если выполняются условия сходимости, то реализуется пошаговое (итерационное) приближение к экстремуму.

Методы оптимизации классифицируют по ряду признаков.

В зависимости от числа управляемых параметров различают методы одномерной и многомерной оптимизации. В методах одномерной оптимизации управляемый параметр единственный, в других размер вектора   не менее двух. Реальные задачи в САПР многомерны, методы одномерной оптимизации играют вспомогательную роль на отдельных этапах многомерного поиска.

Различают методы условной и безусловной оптимизации по наличию или отсутствию ограничений. Для реальных задач характерно наличие ограничений, однако методы безусловной оптимизации также представляют интерес, поскольку задачи условной оптимизации с помощью специальных методов могут быть сведены к задачам без ограничений.

В зависимости от числа экстремумов различают задачи одно- и многоэкстремальные. Если метод ориентирован на определение какого-либо локального экстремума, то такой метод относится к локальным методам. Его называют методом локального поиска. Если же результатом является глобальный экстремум, то метод называют методом глобального поиска. Удовлетворительные по вычислительной эффективности методы глобального поиска для общего случая отсутствуют и потому на практике в САПР используют методы поиска локальных экстремумов.

Наконец, в зависимости от того, используются при поиске производные целевой функции по управляемым параметрам или нет, различают методы нескольких порядков. Если производные не используются, то имеет место метод нулевого порядка, если используются первые или вторые производные, то соответственно метод первого или второго порядка. Методы первого порядка называют также градиентными, поскольку вектор первых производных   по   есть градиент целевой функции

Конкретные методы определяются следующими факторами:

1. способом вычисления направления поиска g(x_k) в формуле (1);

2. способом выбора шага  ;

3. способом определения окончания поиска.

Определяющим фактором является первый из перечисленных в этом списке. Шаг может быть или постоянным, или выбираться исходя из одномерной оптимизации — поиска минимума целевой функции в выбранном направлении  .

Окончание поиска обычно осуществляют по правилу: если на протяжении   подряд идущих шагов траектория поиска остается в малой  -окрестности текущей точки поиска  , то поиск следует прекратить, следовательно, условие окончания поиска имеет вид  .

Методы одномерной оптимизации

Задачи одномерной минимизации представляют собой простейшую математическую модель оптимизации, в которой целевая функция зависит от одной переменной, а допустимым множеством является отрезок вещественной оси:

f(x) -> min , x принадлежит [a, b].

Самым слабым требованием на функцию f(x), позволяющим использовать эти методы, является ее унимодальность. Поэтому далее будем считать функцию f(x) унимодальной на отрезке [a, b]

т.е. на котором имеется один минимум.

К методам одномерной оптимизации относятся методы равномерного поиска, дихотомического деления, золотого сечения, чисел Фибоначчи, полиномиальной аппроксимации и ряд их модификаций.

Метод перебора или равномерного поиска является простейшим из прямых методов минимизации и состоит в следующем.

Разобьем отрезок [a,b] на n равных частей точками деления:

xi=a+i(b-a)/n, i=0,...n

Вычислив значения F(x) в точках xi, путем сравнения найдем точку xm, где m - это число от 0 до n, такую, что

F(xm) = min F(xi) для всех i от 0 до n.

Погрешность определения точки минимума xm функции F(x) методом перебора не превосходит величены Eps=(b-a)/n.

Согласно методу дихотомического деления (рис. 3,а) отрезок делят пополам и в точках, отстоящих от центра   отрезка на величину допустимой погрешности  , рассчитывают значения целевой функции   и  . Если окажется, что  , то минимум находится на отрезке  , если  , то минимум — на  , если   — на  . Таким образом, на следующем шаге вместо отрезка   нужно исследовать суженный отрезок  ,   или  . Шаги повторяются, пока длина отрезка не уменьшится до величины погрешности  . Таким образом, требуется не более  шагов, где   — ближайшее к   целое значение, но на каждом шаге целевую функцию следует вычислять дважды.

Рис. 3.  Одномерная минимизация: а — дихотомическое деление; б — золотое сечение

 Золотое сечение (золотая пропорция) — деление непрерывной величины на две части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине.

Отношение большей части к меньшей в этой пропорции выражается квадратичной иррациональностью

и, наоборот, отношение меньшей части к большей

Геометрическое построение. Золотое сечение отрезка AB можно построить следующим образом: в точке B восстанавливают перпендикуляр к AB, откладывают на нём отрезок BC, равный половине AB, на отрезке AC откладывают отрезок AD, равный AC − CB, и наконец, на отрезке AB откладывают отрезок AE, равный AD. Тогда

Рассмотрим для простоты отрезок [0,1] единичной длины.

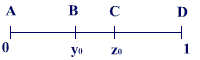
Ясно, что на отрезке имеется две таких точки   и  , они симметричны относительно концов. Точка   производит золотое сечение отрезка [A,C] , а точка   производит золотое сечение отрезка [B,D]. Положим |AB|= x. Тогда |BD|=1-x. В соответствии с определением точки «золотого сечения» имеем:  . Решив эту пропорцию, получим  .

Таким образом, требуется не более   шагов и   вычисление целевой функции, где   можно рассчитать, используя соотношение  при заданной погрешности   определения экстремума.

Согласно методу чисел Фибоначчи, используют числа Фибоначчи  , последовательность которых образуется по правилу   при  , т.е. ряд чисел Фибоначчи имеет вид 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ... Метод аналогичен методу золотого сечения с тем отличием, что коэффициент «а» равен отношению  , начальное значение   определяется из условия, что   должно быть наименьшим числом Фибоначчи, превышающим величину  , где   — заданная допустимая погрешность определения экстремума. Так, если  , то начальное значение  , поскольку  , и  , на следующем шаге будет   и т.д.

Метод полиномиальной аппроксимации: P = a₀+a₁ x +a₂ x²

Выбирают промежуточную точку С на отрезке А,В и записывают значения целевой функции в каждой точке. Далее решают систему из трех АУ, полученных подстановкой P(x) и А, В, С вместо х – получают а_i. Исходя из (dP(x)/dx =0) определяют точку экстремума.

Сравнение эффективности алгоритмов одномерной условной оптимизации.

Аналитическое решение возможнотолько при условии одномерной унимодальной функции Ф(х) на интервале <а, b>. В качестве критерия используют максимальную длину текущего интервала неопределенности (ТИН) после N испытаний.

А) после одной итерации равномерного поиска ТИН уменьшается в N/2 раз

W=(b-a)/N/2

Б) при дихотомическом поиске после одной итерации ТИН уменьшается в 2 раза

W= (b-a)/2ⁿ

B) алгоритм Фибоначчи: i-число Фибоначчи, N-шаг. W= (b-a)/i(N).

В результате:

-при  =14 алгоритм Фибоначчи почти в 3 раз эффективнее алгоритма деления пополам.

-при =14 алгоритм золотого сечения примерно на 40 процентов эффективнее алгоритма Фибоначчи.

http://optimizaciya-sapr.narod.ru/map.html