
- •Глава 2
- •§1 Основные математические понятия.
- •§2 Макроскопические и микроскопические системы. Постулат равновероятности. Эргодическая гипотеза. Статистический вес. Флуктуации.
- •§3 Распределение Больцмана.
- •§4 Распределение Максвелла.
- •§5 Основное уравнение молекулярно-кинетической теории идеальных газов.
- •§6 Функция Больцмана
- •§7 Распределение энергии по степеням свободы.
- •§8 Статистики Ферми-Дирака и Бозе-Эйнштейна.
- •Глава 3. Процессы переноса.
- •§1 Длина свободного пробега, среднее число столкновений.
- •§2 Явления переноса.
- •§3 Молекулярная теория явлений переноса в газах.
- •Глава 4. Реальные жидкости и газы.
- •§1 Силы и потенциальная энергия межмолекулярного взаимодействия.
- •§2. Уравнение Ван-дер-Ваальса
- •§ 3. Изотермы Ван-дер-Ваальса и их анализ.
- •Часть 7—6 — отвечает газообразному состоянию;
- •Часть 2—1 — жидкому;
- •Часть 6—2, — горизонтальный участок, соответствующий равновесию жидкой и газообразной фаз вещества.
- •§ 4. Внутренняя энергия реального газа
- •§ 5. Свойства жидкостей. Поверхностное натяжение
- •§ 6. Смачивание
- •§ 7. Давление под искривленной поверхностью жидкости
- •§ 8. Капиллярные явления
- •§ 9. Испарение, сублимация, плавление и кристаллизация. Аморфные тела
- •§10. Фазовые переходы I и II рода
- •§ 11. Диаграмма состояния. Тройная точка
§3 Распределение Больцмана.
Как мы рассмотрели ранее, микропараметры системы многих частиц являются случайными величинами и для определения их значений нужно знать функции распределения.
Существует различные функции распределения. В классической физике используется классическая статистика Максвелла-Больцмана, в которой движение частиц определяется законами Ньютона, частицы считаются различимыми.
Это распределение частиц по энергиям.
Пусть
система состоит из
материальных точек. Для каждой 3 скорости
и 3 координаты. Разобьем все координатное
пространство и пространство скоростей
на
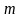 участков и будем определять число частиц
участков и будем определять число частиц
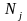 координаты и скорости которых попали
в
координаты и скорости которых попали
в
 участок от
участок от
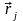 до
до
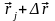 и от
и от
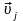 до
до
 .
Энергия частиц
подгруппы:
.
Энергия частиц
подгруппы:
 ,
где
,
где
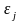 - энергия 1 частицы группы.
- энергия 1 частицы группы.
Энергия
всей системы
 ,
где
,
где

Определим статистический вес состояния из групп по частиц (число размещений). Математика (комбинаторика) дает формулу:
 ,
подставим это выражение в формулу
Больцмана:
,
подставим это выражение в формулу
Больцмана:
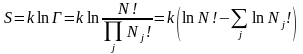 .
.
Учтем формулу Стирлинга для вычисления факториала:
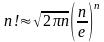 при
при
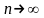
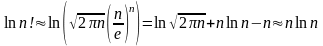
при
величиной
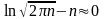 можно пренебречь.
можно пренебречь.
Тогда

У нас идеальный газ находится в фиксированном объеме. Запишем изменение энергии, связанное с тем, что меняется число частиц в группе.
Основное
ТД тождество для открытой системы
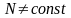 :
:
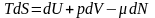
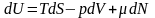 ,
так как
,
так как
 ,
то
,
то
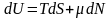
В
нашем случае, изменение внутренней
энергии частиц в группе и изменение
числа частиц в группе связаны:
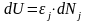 ;
; 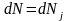 ,
отсюда изменение энтропии, связанное
с тем, что меняется число частиц в
группе:
,
отсюда изменение энтропии, связанное
с тем, что меняется число частиц в
группе:
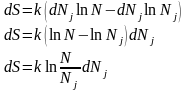
Подставим полученное выражение в основное ТД тождество для открытой изохорической системы:
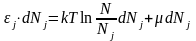 сгруппируем
сгруппируем
 отсюда
отсюда
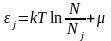 .
Теперь выразим отношение
.
Теперь выразим отношение
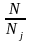 :
:
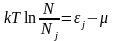 ,
,
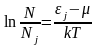
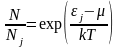 ,
следовательно
,
следовательно
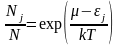
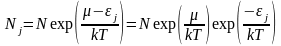 ,
так как величина
,
так как величина
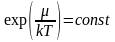 ,
то можно ее обозначить
,
то можно ее обозначить
 ,
тогда с учетом, того что
,
тогда с учетом, того что
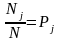 вероятность частицы попасть в
участок, мы получим распределение
Больцмана:
вероятность частицы попасть в
участок, мы получим распределение
Больцмана:
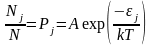 - вероятность того, что молекула идеального
газа имеет энергию
,
т.е. находиться в
-ом
состоянии. Это дискретное распределение,
но его можно сделать непрерывным.
- вероятность того, что молекула идеального
газа имеет энергию
,
т.е. находиться в
-ом
состоянии. Это дискретное распределение,
но его можно сделать непрерывным.
В данном распределении остается скрытой предпосылка осуществления этого распределения – различимости частиц. Эта предпосылка с физической точки зрения ошибочна, потому что в природе нет различимых частиц, и все реально существующие частицы описываются либо распределением Ферми-Дирака, либо распределением Бозе-Эйнштейна. Однако в наиболее часто встречающихся ситуациях классической физики распределения Ферми-Дирака и Бозе-Эйнштейна практически совпадают с распределением Максвелла-Больцмана, которое благодаря этому является основным распределением классической статистической физики.
§4 Распределение Максвелла.
Полная энергия системы равна сумме ее потенциальной и кинетической энергий.
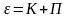

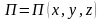
Рассмотрим распределение Больцмана, в котором энергия системы представлена в виде суммы двух слагаемых. По свойству потенциальной функции, выражение можно разложить на произведение двух сомножителей, каждый из которых является функцией определенного вида энергии:
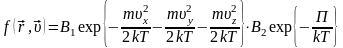
В таком виде выражение называется функцией распределения Максвелла-Больцмана. Сомножитель, зависящий от кинетической энергии, называется функцией Максвелла, а сомножитель, зависящий от потенциальной энергии – функцией Больцмана.
Найдем
вероятность того, что молекула имеет
скорость в интервале
 .
.
Плотность вероятности этого – функция распределения Максвелла.
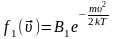
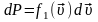
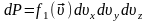
Определим
константу
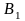 из условия нормировки:
из условия нормировки:
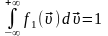
 ,
так как компоненты скорости независимы,
то
,
так как компоненты скорости независимы,
то
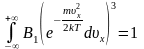 .
Обозначим константу
.
Обозначим константу
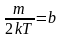 ,
,
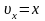 ,
тогда после замены мы получим табличный
интеграл:
,
тогда после замены мы получим табличный
интеграл:
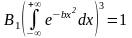 ,
значение интеграла
,
значение интеграла
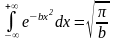 ,
отсюда получим
,
отсюда получим
 ,
следовательно:
,
следовательно:
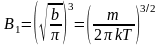 .
.
Таким
образом
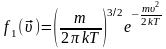 - плотность вероятности молекул иметь
скорость в интервале от
,
распределение молекул по проекциям
координат.
- плотность вероятности молекул иметь
скорость в интервале от
,
распределение молекул по проекциям
координат.
Теперь
найдем вероятность того, что молекулы
имеют скорость в интервале
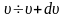 по абсолютному значению (по модулю). Для
этого перейдем от распределения проекций
скоростей к распределению по модулю
скорости. Удобнее переход сделать в
системе сферических координат.
по абсолютному значению (по модулю). Для
этого перейдем от распределения проекций
скоростей к распределению по модулю
скорости. Удобнее переход сделать в
системе сферических координат.
Оператор Лапласа дает коэффициент перехода от декартовой системы координат к сферической:
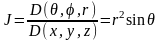 ,
,
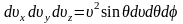
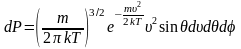
Нас интересуют только абсолютные значения, поэтому:
 ,
с учетом вычисленных интегралов:
,
с учетом вычисленных интегралов:
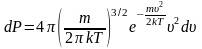 ,
отсюда плотность вероятности:
,
отсюда плотность вероятности:
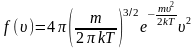
Зная плотность распределения молекул по абсолютному значению скорости, мы можем рассчитать три характеристические скорости движения молекул идеального газа.
Средняя арифметическая скорость:
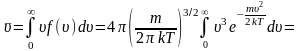 выделим
для замены переменной
выделим
для замены переменной
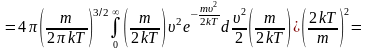
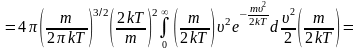 сделаем
замену переменной
сделаем
замену переменной
и
учтем, значение табличного интеграла:
 ,
,
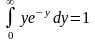 ,
получим после сокращения констант:
,
получим после сокращения констант:
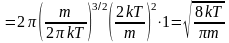 ,
где
,
где
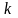 - постоянная Больцмана,
- масса молекулы, преобразуем, умножив
числитель и знаменатель дроби на число
Авогадро:
- постоянная Больцмана,
- масса молекулы, преобразуем, умножив
числитель и знаменатель дроби на число
Авогадро:
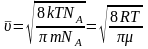 ,
где
,
где
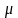 - молярная масса компоненты системы.
- молярная масса компоненты системы.
Результат:
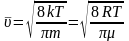 - средняя
арифметическая скорость движения
молекул идеального газа.
- средняя
арифметическая скорость движения
молекул идеального газа.
Средняя квадратичная скорость:
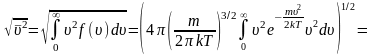 ,
,
сделаем замену переменной:
 ,
тогда
,
тогда
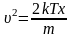 ,
,
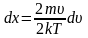 ,
отсюда
,
отсюда
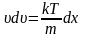 ,
,
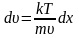 ,
разделим переменные и найдем связь
между
,
разделим переменные и найдем связь
между
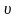 и
и
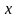
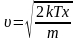 ,
подставим полученное значение в
дифференциал:
,
подставим полученное значение в
дифференциал:
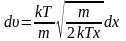 ,
, 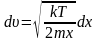 .
.
Подставим все в интеграл:
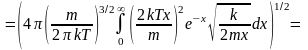 преобразуем,
преобразуем,

 ,
учтем значение табличного интеграла:
,
учтем значение табличного интеграла:
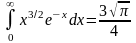
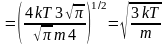 ,
таким образом
,
таким образом
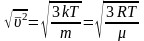 -
средняя
квадратичная скорость.
-
средняя
квадратичная скорость.
Наиболее вероятная скорость:
Наиболее вероятная скорость – это скорость, соответствующая максимуму кривой распределения молекул по скоростям, т.е. должно выполнятся условие:
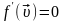
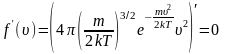
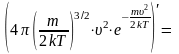 обозначим
константу
обозначим
константу
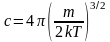 и найдем производную произведения
и найдем производную произведения
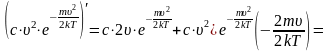
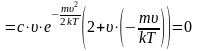
так
как величина
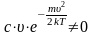 ,
то должно выполняться условие:
,
то должно выполняться условие:
 ,
, 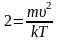 ,
, 
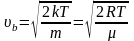 -
скорость
наиболее вероятная.
-
скорость
наиболее вероятная.
П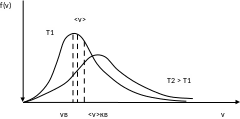 ри
комнатной температуре средняя
арифметическая скорость движения
молекул:
ри
комнатной температуре средняя
арифметическая скорость движения
молекул:
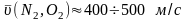 ,
а характеристические скорости водорода
в 4 раза больше.
,
а характеристические скорости водорода
в 4 раза больше.
Как посчитать число молекул, скорости которых лежат в заданном диапазоне?
Если
 - число молекул в единице объема, то
- число молекул в единице объема, то
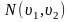 - число молекул, скорости которых
распределены в интервале от
- число молекул, скорости которых
распределены в интервале от
 до
до
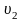 равно:
равно:
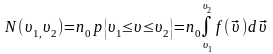 ,
если учесть что
,
если учесть что
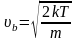 ,
и введя переменные
,
и введя переменные
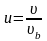 ,
,
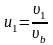 ,
,
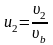 ,
,
 то
то
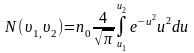 -
такой вид более нагляден, для анализа
формы кривой распределения Максвелла.
В книгах имеются таблицы интеграла:
-
такой вид более нагляден, для анализа
формы кривой распределения Максвелла.
В книгах имеются таблицы интеграла:
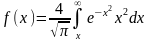 с их помощью упрощаются вычисления
величины
.
с их помощью упрощаются вычисления
величины
.
Из таблиц в частности находим, что:
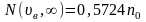
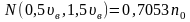
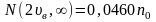
Т.о. большая часть молекул имеет скорости в сравнительно небольшом интервале около наиболее вероятной, а молекул со скоростями вне этого интервала сравнительно мало.
Для
экспериментальной проверки было
проделано много опытов. Самый известный
– опыт Штерна (1920). На оси двух коаксиальных
цилиндров ( и
и
 )
расположена платиновая нить, покрытая
слоем
)
расположена платиновая нить, покрытая
слоем
 .
Нить нагревали током, серебро испарялось,
и его атомы хаотично вылетали по всем
радиальным направлениям. При этом они
имели и различные скорости движения.
Воздух внутри цилиндров откачивался,
чтобы столкновения молекул серебра с
молекулами воздуха не искажали картину.
Атомы серебра равномерно покрывали
поверхность внешнего цилиндра, что
указывало на равновероятность всех
направлений их скорости. Затем во
внутреннем цилиндре - узкая щель,
диафрагмирующая пучок атомов по
направлению (скорости любые по величине).
Внешний цилиндр приводили во вращение
(
.
Нить нагревали током, серебро испарялось,
и его атомы хаотично вылетали по всем
радиальным направлениям. При этом они
имели и различные скорости движения.
Воздух внутри цилиндров откачивался,
чтобы столкновения молекул серебра с
молекулами воздуха не искажали картину.
Атомы серебра равномерно покрывали
поверхность внешнего цилиндра, что
указывало на равновероятность всех
направлений их скорости. Затем во
внутреннем цилиндре - узкая щель,
диафрагмирующая пучок атомов по
направлению (скорости любые по величине).
Внешний цилиндр приводили во вращение
(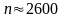 )
об/мин.
)
об/мин.
В зависимости от скорости атомы попадают на разные участки поверхности вращающегося цилиндра, согласно формуле на участок АВ:

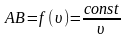 .
.
Чем
больше атомов осаждается на стенке, тем
толще пленка. Измеряя толщину пленки,
можем определить число атомов, обладающих
скоростью, лежащей в некотором диапазоне,
т.е. построить диаграмму, которая при
сглаживании схожа с кривой распределения
Максвелла
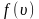 .
.
